本文内容:C语言实现并附有相关讲解
- 计算中缀表达式
- 计算后缀表达式
- 计算前缀表达式
- 中缀转后缀表达式
- 中缀转前缀表达式
相关链接:
【例子】
| 表达式 | 例子 |
|---|---|
| 表达式(中缀) | |
| 前缀 | |
| 后缀 |
【计算结果】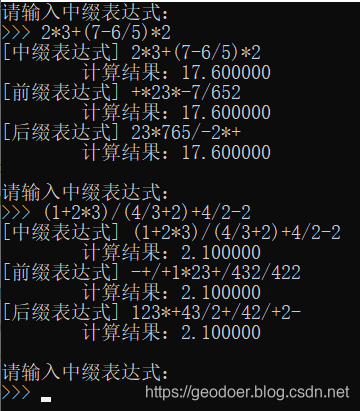
【代码】
#include<stdio.h>#include<string.h>// 计算float Cal(float a, char op, float b) {switch (op) {case '+' : return (a+b);case '-' : return (a-b);case '*' : return (a*b);case '/' : return (a/b);}return 0;}/*-----------------------|计算中缀表达式 |-----------------------*//*数据结构:两个栈,一个存放操作数(stack1),一个存放运算符(stack2)操作步骤:1. 从左到右扫描中缀表达式若是数字,直接入stack1若是字符:若运算符栈为空,直接入栈stack2若栈不为空,则要与stack2的栈顶的优先级进行比较若当前字符为左括号,则压入stack2栈中若当前字符为右括号,则从stack2中取出运算符,再从stack1栈中取出两个数字进行运算,运算结果压入stack1中;直到栈顶元素为左括号,将左括号弹出即可(即右括号与左括号做抵消)若当前字符的优先级小于栈顶,则将栈顶元素抛出,从操作数栈中取两个数字进行运算,运算结果压入操作数栈。继续判断此字符与栈顶元素优先级大小,直到栈顶元素优先级小于此字符若当前字符的优先级大于栈顶,则将此字符直接压入运算符栈中2. 最后,若栈中还有元素,取出继续计算函数:1. CalInfix(str[]):传入中缀表达式,返回计算结果2. Cal_from_stack12:上述步骤中,重复的操作即是从stack1中取操作数,stack2中取运算符进行运算,最后将结果压入stack1中。因此将这些操作封装成函数简化代码,增加可读性*/float Cal_from_stack12(float stack1[], int &top1, char stack2[], int &top2) {// stack1为数字的栈、stack2为运算符的栈// 从两个栈中计算char op = stack2[top2--];float b = stack1[top1--];float a = stack1[top1--];float ret = Cal(a, op, b);stack1[++top1] = ret;return ret;}float CalInfix(char str[]) { //计算中缀表达式float stack1[100]; int top1=-1; //存放数字的栈char stack2[100]; int top2=-1; //存放运算符的栈int i;// 遍历中缀表达式for (i=0; str[i]!='\0'; ++i) {// str[i]是数字,直接入栈,后退出此次循环if (str[i]<='9' && str[i]>='0') { // str[i]数字stack1[++top1]=(float)(str[i]-'0');continue;}//str[i]是字符(运算符)// 运算符的栈为空,直接入栈if (top2==-1) {stack2[++top2] = str[i];continue;}// 运算符的栈不为空,要比较和栈顶的优先级if (str[i]=='+' || str[i]=='-') { // 当前运算符为+、-,那么比+、-、*、/优先级都小,所以要让它们都先计算完才能入栈while (stack2[top2]=='+' || stack2[top2]=='-' || stack2[top2]=='*' || stack2[top2]=='/') {Cal_from_stack12(stack1, top1, stack2, top2); //计算}stack2[++top2]=str[i]; //运算完后,str[i]入栈} else if (str[i]=='*' || str[i]=='/') { // 只有*、/计算完后,才能入栈while (stack2[top2]=='*' || stack2[top2]=='/') {Cal_from_stack12(stack1, top1, stack2, top2); //计算}stack2[++top2]=str[i]; //运算完后,str[i]入栈} else if (str[i]=='(') { //左括号,直接入栈stack2[++top2]=str[i];} else if (str[i]==')') { //右括号,处理到把'('抵消while (stack2[top2]!='(') {Cal_from_stack12(stack1, top1, stack2, top2); //计算}top2--; //弹出左括号}}// 遍历完成后,检查栈是否计算完while (top2!=-1) {Cal_from_stack12(stack1, top1, stack2, top2); //计算}return stack1[top1]; //返回计算结果}/*-------------------------|中缀表达式 转 前缀表达式|-------------------------*//*数据结构:1. 一个栈stack:用于存运算符2. 一个数组tmp:用于暂时存储输出结果,这个结果实际是前缀表达式的逆序。即结束后,将此数组逆置就获得了前缀表达式算法步骤:从右至左扫描中缀表达式若是操作数,直接输出到tmp数组中若是运算符,查看栈顶若是右括号,直接压入栈中若是左括号,将栈元素弹出输出到tmp数组中,直到抵消到栈中的右括号若此运算符优先级小于栈顶元素,则栈内元素出栈并输出到tmp数组中,直到该运算符优先级大于等于栈顶元素,再将其压入栈中否则,则该运算符直接入栈最后将栈中剩余元素输出到tmp中,结束后,将tmp数组翻转*/int infix_to_prefix(char in[], char pre[]) {char stack[100]; int top=-1; //用于存放运算符char tmp[100]; int j=0; //存放暂时的结果,即前缀表达式的逆序int i;for (i=strlen(in)-1; i>=0; --i) { //从右到左扫描中缀表达式if ('0' <= in[i] && in[i] <= '9') { //操作数,直接输出tmp[j++] = in[i];} else if (in[i]==')') {stack[++top] = in[i];} else if (in[i]=='(') {while (stack[top]!=')') {tmp[j++] = stack[top--];}--top; //左括号出栈} else if (in[i]=='+' || in[i]=='-') {while (stack[top]=='*' || stack[top]=='/') {tmp[j++] = stack[top--];}stack[++top] = in[i];} else if (in[i]=='*' || in[i]=='/') {stack[++top] = in[i];} else {return 0;}}// 输出剩余东西while (top!=-1) {tmp[j++] = stack[top--];}// 逆置i=0;for (i=0, j=j-1; j>=0; ++i,--j) {pre[i] = tmp[j];}pre[i]='\0';return 0;}/*-----------------------|计算前缀表达式:波兰式|-----------------------*//*从左到右遍历前缀表达式若遇到操作符,入栈若遇到操作数,查看栈顶若栈顶是操作符,入栈;若栈顶是操作数,则将操作数出栈,再出栈一个操作符,进行运算,运算后继续判断栈顶情况,直到栈顶不是操作数或栈空再将结果入栈*/typedef struct{union{char op;float num;}data;int flag; //0为操作数,1为num}StackNode; //栈的结点float CalPrefix(char str[]) {// 默认:前缀表达式合法StackNode stack[100]; int top=-1; //用于存放操作数和操作符的栈char op;float a,result;int i;for (i=0; str[i]!='\0'; ++i) {if ('0' <= str[i] && str[i] <='9') { //数字if ( top==-1 || stack[top].flag!=1 ) { // 栈顶为空 或 栈顶不是数字,直接入栈++top; stack[top].flag=1; stack[top].data.num = (float)(str[i]-'0'); //数字入栈continue; //此次循环处理结束!}result = (float)(str[i]-'0'); //获得当前的数字while (top!=-1 && stack[top].flag==1) { // 栈顶如果是数字,一直判断到不是数字a = stack[top--].data.num; //在栈中取一个操作数op = stack[top--].data.op; //在栈中取一个运算符result = Cal(a, op, result); //计算}++top; stack[top].flag=1; stack[top].data.num = result; //将此轮计算结果入栈} else { //操作符++top; stack[top].flag=0; stack[top].data.op = str[i];}}return stack[top].data.num;}/*-------------------------|中缀表达式 转 后缀表达式|-------------------------*/int infix_to_suffix(char in[], char suf[]) {char stack[100]; int top=-1; //运算符的栈int i, j;j=0; //suf[]的指针for (i=0; in[i]!='\0'; ++i) { //遍历in// 是数字if ('0' <= in[i] && in[i] <= '9') {suf[j++] = in[i];continue;}// 是符号if (top==-1) { //栈为空stack[++top] = in[i];continue;}// 栈不为空if (in[i]=='+' || in[i]=='-') {while (stack[top]=='+' || stack[top]=='-' || stack[top]=='*' || stack[top]=='/') {suf[j++] = stack[top--];}stack[++top] = in[i];} else if (in[i]=='*' || in[i]=='/') {while (stack[top]=='*' || stack[top]=='/') {suf[j++] = stack[top--];}stack[++top] = in[i];} else if (in[i]=='(') {stack[++top] = in[i];} else if (in[i]==')') {while (stack[top]!='(') {suf[j++] = stack[top--];}top--; //将栈中'('输出} else {suf[0]='\0';return -1;}}// 输出剩下的符号while (top!=-1) {suf[j++] = stack[top--];}suf[j]='\0';return 1; //转换成功}/*-------------------------|计算后缀表达式:逆波兰式|-------------------------*/float CalSuffix(char str[]) {float stack[100]; int top=-1; //存放数字int i;float a,b;for (i=0; str[i]!='\0'; ++i) {if ('0' <= str[i] && str[i] <= '9') { //数字stack[++top]=(float)(str[i]-'0');} else { //不是数字b=stack[top--];a=stack[top--];stack[++top]=Cal(a, str[i], b);}}return stack[top];}/* 例子表达式(中缀):2*3+(7-6/5)*2前缀: +*23*-7/652后缀: 23*765/-2*+测试数据:2*3+(7-6/5)*2(1+2*3)/(4/3+2)+4/2-2*/int main() {char in[100], suf[100], pre[100];for ( ; ; ) {// 输入中缀表达式printf("请输入中缀表达式:\n>>> ");scanf("%s", in);// CalInfix()函数测试printf("[中缀表达式] %s\n", in);printf("\t计算结果:%lf\n", CalInfix(in) );// 前缀表达式infix_to_prefix(in, pre);printf("[前缀表达式] %s\n", pre);printf("\t计算结果:%lf\n", CalPrefix(pre) );// 后缀表达式infix_to_suffix(in, suf);printf("[后缀表达式] %s\n", suf);printf("\t计算结果:%lf\n", CalSuffix(suf) );printf("\n");}return 0;}

