二叉堆

【堆】一种数据结构，可以是n叉

【二叉堆】可以把堆看成是一颗完全二叉树

1. 【堆顶】堆的根结点称为堆顶，且根结点的权值是最值
2. 任何一个非叶子结点的值都不大于（或不小于）其左右孩子结点的值 | 分类 | 说明 | 图 | | —- | —- | —- | | 大顶堆
   （最大堆） | 父亲大孩子小；
   根结点是最大值 |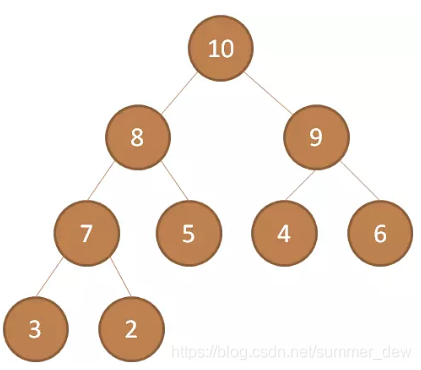 | | 小顶堆
   （最小堆） | 孩子大父亲小；
   根结点是最小值 | |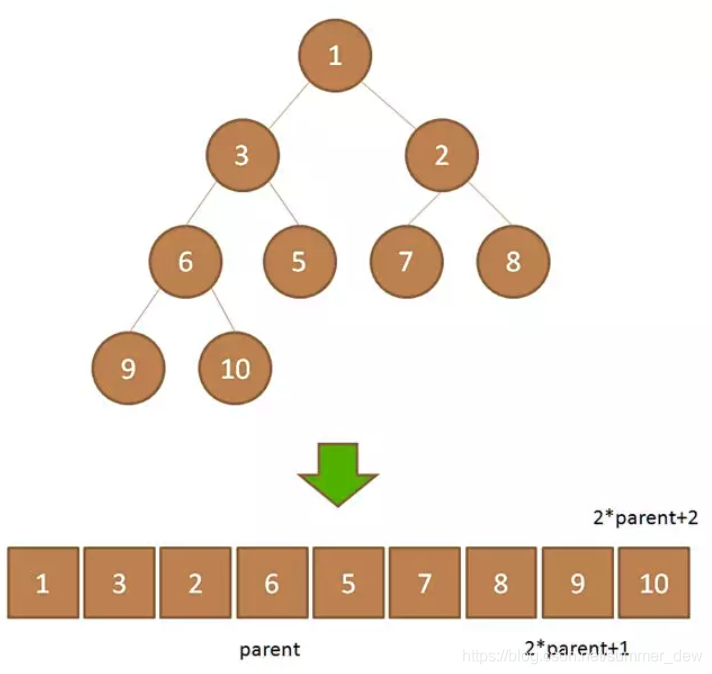

构建二叉堆

【构建二叉树】把无序的完全二叉树调整为二叉堆
【做法】让所有非叶子结点依次下沉

示例（最小堆）	说明
无序的完全二叉树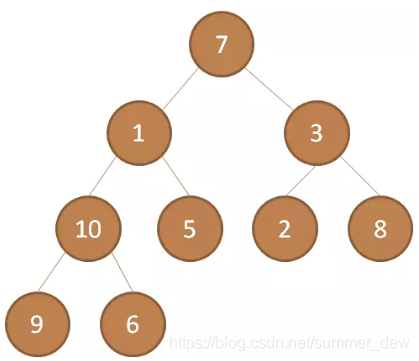
从最后一个非叶子结点p开始	从10开始，如果10＞左右孩子，取最小的一个，下沉。重复处理10，直到下沉不了了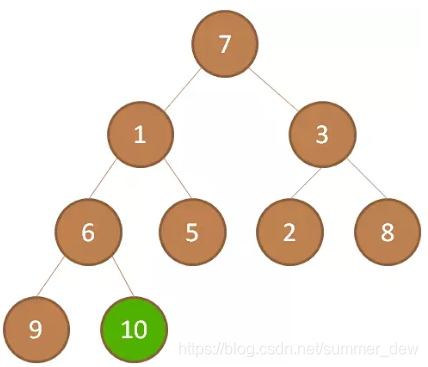
p前移一位	轮到节点3，和上面一样，下沉。重复处理结点3，直到下沉不了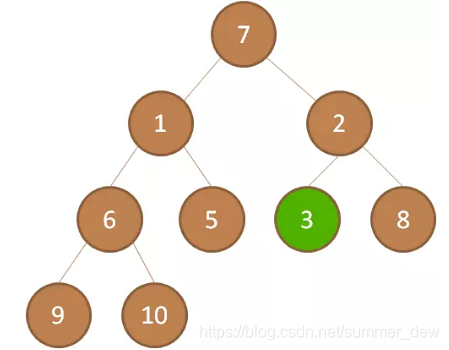
p前移一位	轮到结点1，但结点1<6,1<5，不做处理
p前移一位	轮到节点7，比较7的孩子，取最小的那个孩子，下沉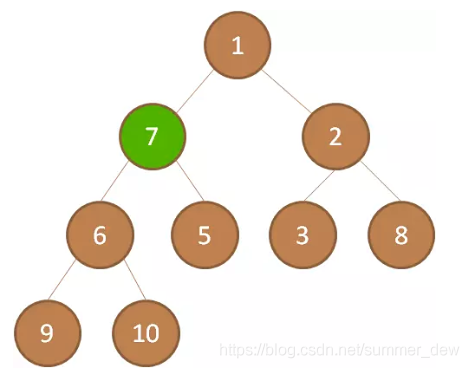
p前移一位	继续处理7，直到下沉不了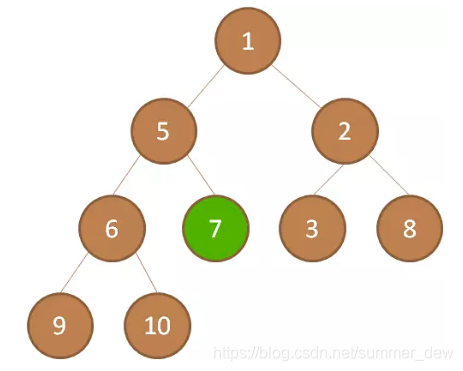
直到处理完所有的结点

插入结点

【插入结点】插在最后一个位置；然后和父亲比较；不满足条件就上浮

示例（最小堆）	说明
在最后一位插入新结点	插入一个新结点0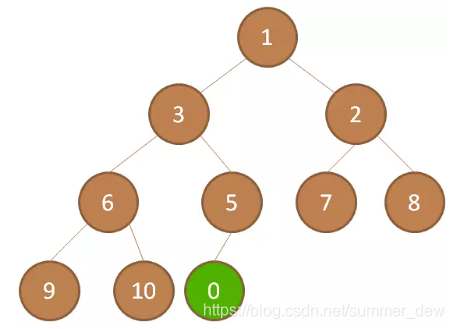
上浮	结点0和它的父节点5比较：0<5，上浮（和父节点交换位置）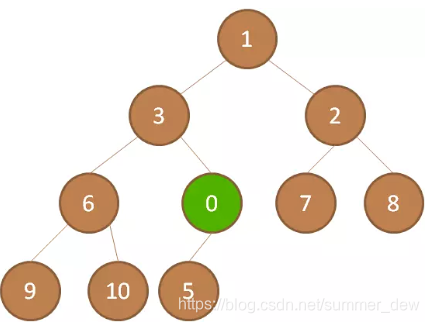
	继续和父亲比较：0＜3，继续上浮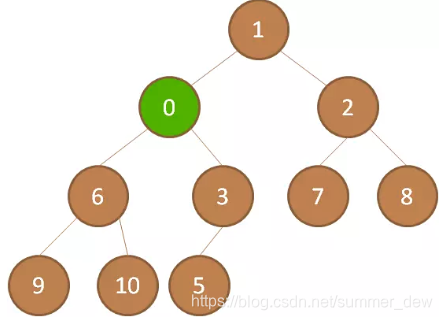
上浮至满足条件	最终浮到了堆顶位置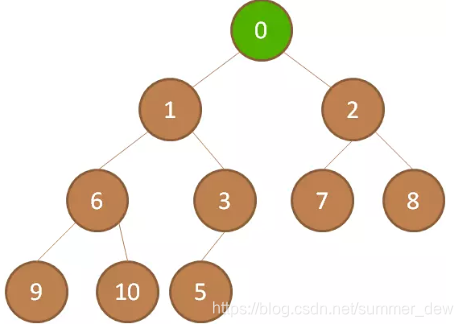

删除结点

【删除结点】删除堆顶的结点；把最后一个结点补充到堆顶；对堆顶进行下沉处理

示例（最小堆）	说明
删除堆顶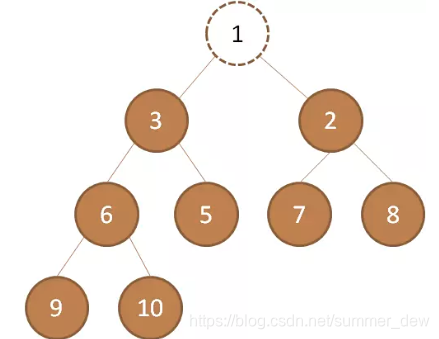
把最后一个节点补上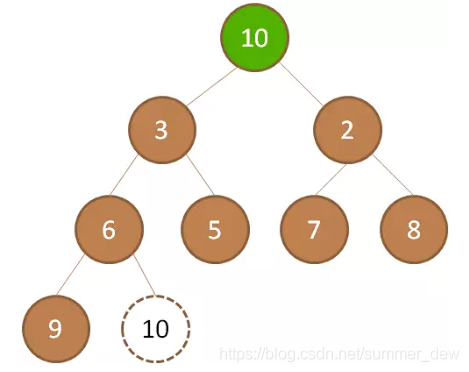
让新结点下沉	10和它左右孩子比较：10<3，10<2，2<3；取最小的那个孩子2，下沉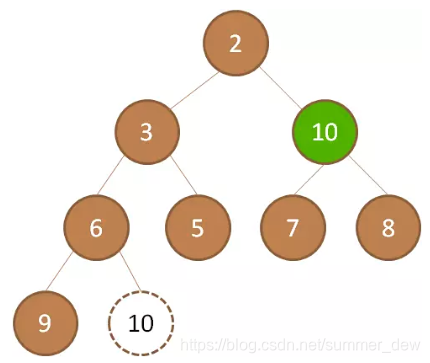
继续下沉，直到满足堆的条件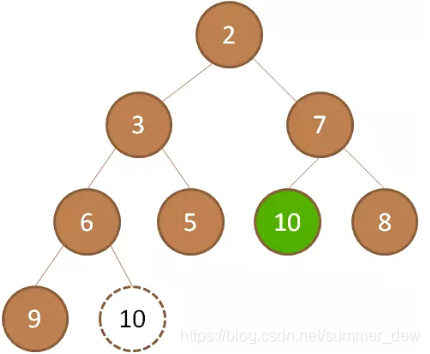

堆排序

【堆排序】堆排序是简单选择排序的改良版，它使用堆这种数据结构重复利用了之前的比较结果，减少了时间复杂度

【思想】用堆来选择出每趟的最值；再交换到无序序列的边界上，让它归入到有序序列

【堆排序过程】①建堆；②删除结点，加入到有序序列中；③重复②，直到堆（无序序列）中无元素

代码

【完全二叉树的顺序存储】

下标从0开始	下标从1开始
n=6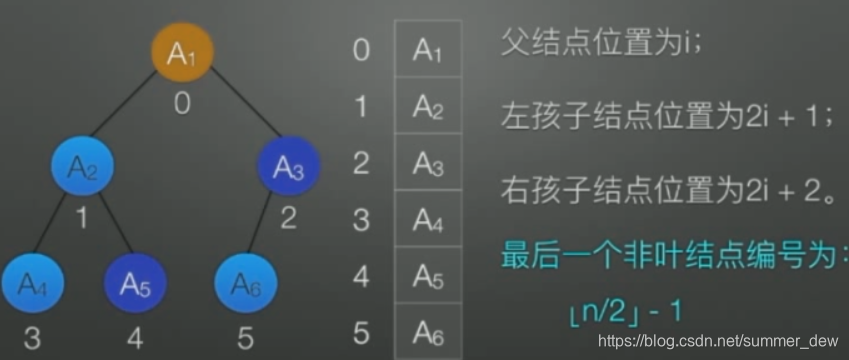	n=10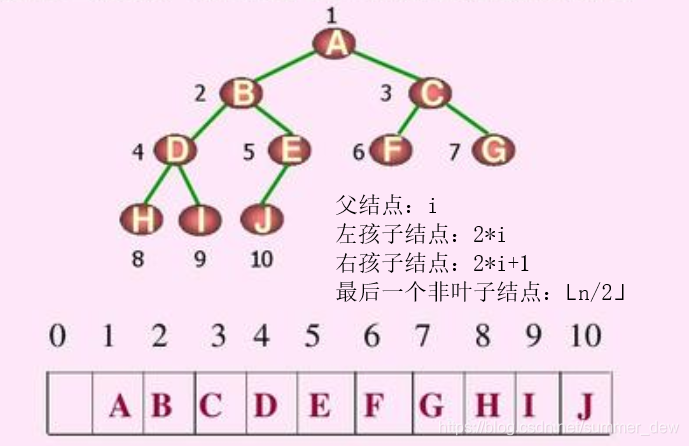

用小顶堆进行从大到小排序

/* arr[]中元素从0开始存储 */
// 若arr[low]不满足堆定义，则在[low, high]范围内调整（下沉）
void Sift(int arr[], int low, int high) {
    int i=low;
    int j=2*i+1; //i的左孩子
    int tmp=arr[i]; //将要调整的元素备份
    while (j<=high) {
        //左右孩子取更小的那个（小顶堆）
        if (j<high && arr[j]>arr[j+1]) //右孩子比较小
            ++j; //把j指向右孩子
        if (tmp>arr[j]) { //元素>它的孩子（小顶堆）
            //元素下沉
            arr[i]=arr[j];
            i=j;//i为元素下沉之后的位置
            j=2*i+1; //j为i的左孩子
        } else //元素<它的孩子（小顶堆）：调整结束
            break;
    }
    arr[i]=tmp; //i记为元素调整之后的位置
}
// 堆排序（从大到小排序）：arr[]从0开始存储
void HeapSort(int arr[], int n) {
    int i,tmp;
    // 从最后一个非叶子结点开始调整
    for (i=n/2-1; i>=0; --i)
        Sift(arr, i, n-1);
    // 堆排序
    for (i=n-1; i>=1; --i) { //从小顶堆中取n-1次堆顶
        // 堆顶和堆尾交换
        tmp=arr[0]; //取出堆顶
        arr[0]=arr[i]; //堆的最后一个元素放到堆顶
        arr[i]=tmp; //把此趟的最值放入堆的最后一个位置
        // arr[i]即变成了有序序列
        Sift(arr, 0, i-1); //调整[0, i-1]
    }
}

用大顶堆进行从小到大排序

/* arr[]中元素从0开始存储 */
// 若arr[low]不满足堆定义，则在[low, high]范围内调整（下沉）
void Sift(int arr[], int low, int high) {
    int i=low;
    int j=2*i+1; //i的左孩子结点
    int tmp=arr[i]; //把将要调整的元素备份
    while (j<=high) {
        // 大顶堆 -> 左右孩子中取更大的那个
        if (j<high && arr[j]<arr[j+1] ) //右孩子比较大
            ++j; //把j指向右孩子
        if (tmp<arr[j]) { //元素<它的孩子（大顶堆）
            //元素下沉
            arr[i]=arr[j];
            i=j; //i为元素下沉之后的位置
            j=2*i+1; //j为i的左孩子
        } else { //元素>它的孩子：调整结束
            break;
        }
    }
    arr[i]=tmp; //i记为元素调整之后的位置
}
// 堆排序（从小到大排序）：arr[]从0开始存储
void HeapSort(int arr[], int n) {
    int i, tmp;
    // 从最后一个非叶子结点开始调整
    for (i=n/2-1; i>=0; --i) //最后一个结点n的父亲    
        Sift(arr, i, n-1);
    // 堆排序
    for (i=n-1; i>=1; --i) { //从大顶堆中取n-1次最值
        // 堆顶和堆尾交换
        tmp=arr[0]; //从大顶堆中取出堆顶（最大值）
        arr[0]=arr[i];//将堆中最后一个元素放在堆顶
        arr[i]=tmp; //将最大值放入大顶堆的最右边
        // arr[i]即加入了有序序列
        Sift(arr, 0, i-1); //调整[0, i-1]->大的在右边->从小到大排序
    }
}

评价

【时间复杂度】O(nlog2n)

1. 对于Sift()函数，显然j走了一条从当前结点到叶子结点的路径，完全二叉树的高度为 ⌈log2(n+1) ⌉
   即对每个结点调整的时间复杂度为O(log2n)
2. 对于heapSort()函数，基本操作总次数应该是两个序列的for循环中基本操作次数相加
   • 第一个循环的基本操作次数为O(log2n)*n/2
   • 第二次循环的基本操作次数为O(log2n)*(n-1)
3. 整个算法：O(log2n)*n/2 + O(log2n)*(n-1)=O(nlog2n)

【空间复杂度】O(1)
堆排序所用的堆（二叉树），是在数组的本身上进行的，没有用什么辅助空间

【评价】

1. 堆排序在最坏情况下的时间复杂度也是O(nlog2n)，这是相对快速排序的最大优点
2. 堆排序的空间复杂度O(1)，在所有时间复杂度为O(nlog2n)中是最小的
3. 堆排序适合的场景是关键字数很多的情况，如果记录数较少，则不提倡使用

【经典例子】从10 000个关键字中选出前10个最小的

参考文章

1. 天勤数据结构高分笔记