非递归

【非递归方法】

  1. 思路一：根据访问次序来入栈并输出
  2. 思路二：模拟访问过程
  3. 思路三：使用标识符mark来记录已经第几次访问该结点

【思路一】根据访问次序来入栈并输出

  1. // - 思路一：根据访问次序来入栈并输出
  2. // -- 缺点：没有模拟遍历的实质--对一个结点的三次的访问
  3. void PreOrderNonrecursive1(BiTree T) { //先序遍历
  4.     /*方法原理：
  5.         1. 先序：根左右
  6.         2. 访问根，然后把右、左入栈（先入栈后输出，所以将右子树先入栈）
  7.     */
  8.     BiTNode *p;
  9.     BiTNode *Stack[maxSize]; //自己实现栈，适合做题
  10.     int top=-1; //top指向当前元素
  12.     if (!T) return ;
  13.     Stack[++top] = T; //根结点入栈
  14.     while (top!=-1) {
  15.         p = Stack[top--];
  16.         visit(p->data);
  17.         // 右孩子先入栈，先入栈后输出
  18.         if (p->rchild) Stack[++top]=p->rchild; //把右孩子入栈
  19.         if (p->lchild) Stack[++top]=p->lchild; //把左孩子入栈
  20.     }
  21. }
  22. void PostOrderNonrecursive1(BiTree T) {
  23.     /* 方法原理：
  24.     思路：
  25.         1. 先序：根左右
  26.         2. 后序：左右根 --> 逆后序：根右左
  27.         3. 比较【先序】和【逆后序】：发现根是一样的，只是左右换了一下
  28.     结论：
  29.         1. 与PreOrderNonrecursive1方法类似，只是先将左孩子先入栈（先入栈后输出），得到逆后序序列
  30.         2. 将逆后序数列倒过来输出
  31.     */
  32.     BiTNode *p;
  33.     BiTNode *Stack[maxSize]; int top1=-1;
  34.     BiTNode *InPostOrderStack[maxSize]; int top2=-1;
  35.     Stack[++top1] = T;
  36.     while (top1!=-1) {
  37.         p = Stack[top1--];
  38.         InPostOrderStack[++top2]=p;
  39.         if (p->lchild) Stack[++top1]=p->lchild;
  40.         if (p->rchild) Stack[++top1]=p->rchild;
  41.     }
  42.     while (top2!=-1) {
  43.         p = InPostOrderStack[top2--];
  44.         visit(p->data);
  45.     }
  46. }

【思路二】模拟访问过程

  1. // - 思路二：模拟访问过程
  2. // -- 步骤：走到最左下角，直到走不通-->退回去，往右走一步-->往复
  3. // -- 缺点：只模拟出前两次访问，没有模拟出最后一次访问-->所以该方法不能实现后序遍历
  4. void PreOrderNonrecursive2(BiTree T) { //先序遍历
  5.     BiTNode *Stack[maxSize];int top=-1; //SqStack S;
  6.     BiTNode *p;
  8.     Stack[++top]=T;//Push(&S, T);
  9.     while (top!=-1) { //栈不为空
  10.         //向左走到尽头
  11.         while (p=Stack[top]) {
  12.             visit(p->data);
  13.             Stack[++top]=p->lchild;
  14.         }
  15.         --top; //上一步多将一个NULL放入栈了，删除它
  16.         if (top!=-1) { //退一步，并向右走一步
  17.             p=Stack[top--];
  18.             Stack[++top]=p->rchild;
  19.         }
  20.     }
  21. }
  22. Status InOrderNonrecursive2_1(BiTree T) { //中序遍历
  23.     BiTNode *p;
  24.     BiTNode *Stack[maxSize];int top=-1; //创建栈
  26.     Stack[++top]=T; //根指针进栈
  27.     while (top!=-1) {
  28.         while (p=Stack[top]) Stack[++top] = p->lchild;//向左走到尽头
  29.         --top;//空指针出栈
  30.         if (top!=-1) {//访问结点，向右一步
  31.             p=Stack[top--];
  32.             visit(p->data);
  33.             Stack[++top]=p->rchild;
  34.         }
  35.     }
  36.     return OK;
  37. }
  38. Status InOrderNonrecursive2_2(BiTree T) { //中序遍历
  39.     BiTNode *p;
  40.     BiTNode *Stack[maxSize];int top=-1; //创建栈
  42.     p=T;
  43.     while (p || top!=-1 ) {
  44.         if (p) { //根指针进栈，遍历左子树
  45.             Stack[++top]=p;
  46.             p=p->lchild;
  47.         } else { //根指针退栈，访问根结点，遍历右子树
  48.             p=Stack[top--];
  49.             visit(p->data);
  50.             p=p->rchild;
  51.         }
  52.     }
  53.     return OK;
  54. }

【思路三】使用标识符mark来记录已经第几次访问该结点

  1. // - 思路三：使用标识符mark来记录已经第几次访问该结点
  2. // -- 优点：该方法可以模拟出遍历的实质--同一个结点将会三次访问 --> 可以完成三种遍历的任何一种
  3. // -- 缺点：构造了一个结构体，开销大
  4. typedef struct{
  5.     BiTNode *ptr;
  6.     enum {ZERO, ONE, TWO} mark; // 标识第几次访问
  7. }PMType; //有mark域的结点指针类型
  8. void PreOrderNonrecursive3(BiTree T) { //先序遍历
  9.     PMType pm;
  10.     PMType stack[maxSize];int top=-1; //栈
  12.     pm.mark=ZERO;pm.ptr=T;stack[++top]=pm; //根结点入栈
  13.     while (top!=-1) { //栈不空
  14.         pm = stack[top--]; //取出栈顶
  15.         switch (pm.mark) {
  16.         case ZERO: //第一次访问该结点
  17.             visit(pm.ptr->data);
  18.             pm.mark=ONE;stack[++top]=pm; //修改mark域，再放入栈
  19.             if (pm.ptr->lchild) {//往左走
  20.                 pm.mark = ZERO;pm.ptr=pm.ptr->lchild;
  21.                 stack[++top] = pm;
  22.             }
  23.             break;
  24.         case ONE: //左子树处理返回，第二次访问
  25.             pm.mark=TWO;stack[++top]=pm; //修改mark域，再放入栈
  26.             if (pm.ptr->rchild) { //往右走
  27.                 pm.mark=ZERO;pm.ptr=pm.ptr->rchild;
  28.                 stack[++top]=pm;
  29.             }
  30.             break;
  31.         case TWO: //右子树处理访问，第三次访问
  32.             break; //空操作
  33.         }
  34.     }
  35. }
  36. void InOrderNonrecursive3(BiTree T) { //中序遍历
  37.     PMType pm;
  38.     PMType stack[maxSize];int top=-1; //栈
  40.     pm.mark=ZERO;pm.ptr=T;stack[++top]=pm; //根结点入栈
  41.     while (top!=-1) { //栈不空
  42.         pm = stack[top--]; //取出栈顶
  43.         switch (pm.mark) {
  44.         case ZERO: //第一次访问该结点
  45.             pm.mark=ONE;stack[++top]=pm; //修改mark域，再放入栈
  46.             if (pm.ptr->lchild) {//往左走
  47.                 pm.mark = ZERO;pm.ptr=pm.ptr->lchild;
  48.                 stack[++top] = pm;
  49.             }
  50.             break;
  51.         case ONE: //左子树处理返回，第二次访问
  52.             visit(pm.ptr->data);
  53.             pm.mark=TWO;stack[++top]=pm; //修改mark域，再放入栈
  54.             if (pm.ptr->rchild) { //往右走
  55.                 pm.mark=ZERO;pm.ptr=pm.ptr->rchild;
  56.                 stack[++top]=pm;
  57.             }
  58.             break;
  59.         case TWO: //右子树处理访问，第三次访问
  60.             break; //空操作
  61.         }
  62.     }
  63. }
  64. void PostOrderNonrecursive3(BiTree T) { //后序遍历
  65.     PMType pm;
  66.     PMType stack[maxSize];int top=-1; //栈
  68.     pm.mark=ZERO;pm.ptr=T;stack[++top]=pm; //根结点入栈
  69.     while (top!=-1) {
  70.         pm = stack[top--];
  71.         switch (pm.mark) {
  72.         case ZERO: //刚刚访问此结点
  73.             pm.mark=ONE;stack[++top]=pm; //修改mark域
  74.             if (pm.ptr->lchild) {
  75.                 pm.mark = ZERO;pm.ptr = pm.ptr->lchild;
  76.                 stack[++top] = pm; //访问左子树
  77.             }
  78.             break;
  79.         case ONE: //左子树处理返回
  80.             pm.mark=TWO;stack[++top]=pm; //修改mark域
  81.             if (pm.ptr->rchild) {
  82.                 pm.mark = ZERO;pm.ptr=pm.ptr->rchild;
  83.                 stack[++top] = pm; //访问右子树
  84.             }
  85.             break;
  86.         case TWO: //右子树处理返回
  87.             visit(pm.ptr->data);
  88.         }
  89.     }
  90. }

完整代码（包括递归）

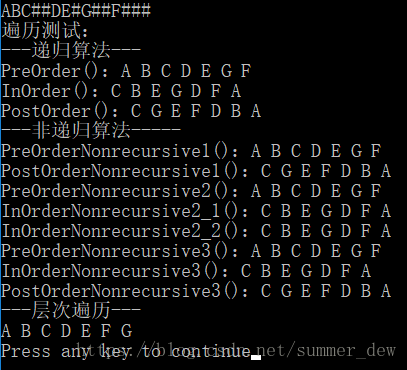
二叉树遍历 - 图1

/*
@Desc:二叉链表 无头结点
@Vesrion:0.0.1
@Time:20180922创建
*/

#include<stdio.h>
#include<stdlib.h>

#ifndef BASE
#define BASE
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int bool;
#endif

#define TElemType char //固定为char，若修改需要修改方法
typedef struct BiTNode { // 结点结构
    TElemType      data;
    struct BiTNode  *lchild, *rchild; // 左右孩子指针
}BiTNode, *BiTree;
void visit(TElemType e) {
    printf("%c ", e);
}

#define maxSize 50 //本文件中 队列、栈 最大的内容


Status PreCreate(BiTree *pT); // 先序遍历创建二叉树
int BiTreeDepth(BiTree T); // 求二叉树深
void LevelOrder(BiTree T);// 层次遍历DFS

// ----------------------------- 遍历 递归实现
void PreOrder(BiTree T); // 先序遍历二叉树
void InOrder(BiTree T); // 中序遍历二叉树
void PostOrder(BiTree T); // 后序遍历二叉树

// ----------------------------- 遍历 非递归实现
// - 思路一：根据访问次序来入栈并输出
// -- 缺点：没有模拟遍历的实质--对一个结点的三次的访问
void PreOrderNonrecursive1(BiTree T); //先序遍历
void PostOrderNonrecursive1(BiTree T); //后序遍历

// - 思路二：模拟访问过程
// -- 步骤：走到最左下角，直到走不通-->退回去，往右走一步-->往复
// -- 缺点：只模拟出前两次访问，没有模拟出最后一次访问-->所以该方法不能实现后序遍历
void PreOrderNonrecursive2(BiTree T); //先序遍历
Status InOrderNonrecursive2_1(BiTree T); //中序遍历-第一种
Status InOrderNonrecursive2_2(BiTree T); //中序遍历-第二种

// - 思路三：使用标识符mark来记录已经第几次访问该结点
// -- 优点：该方法可以模拟出遍历的实质--同一个结点将会三次访问 --> 可以完成三种遍历的任何一种
// -- 缺点：构造了一个结构体，开销大
typedef struct{
    BiTNode *ptr;
    enum {ZERO, ONE, TWO} mark; // 标识第几次访问
}PMType; //有mark域的结点指针类型
void PreOrderNonrecursive3(BiTree T); //先序遍历
void InOrderNonrecursive3(BiTree T); //中序遍历
void PostOrderNonrecursive3(BiTree T); //后序遍历

int main() {
    BiTree T;

    PreCreate(&T); //测试数据：ABC##DE#G##F###
    printf("遍历测试：\n");
    printf("---递归算法---\n");
    printf("PreOrder()：");PreOrder(T);printf("\n");
    printf("InOrder()：");InOrder(T);printf("\n");
    printf("PostOrder()：");PostOrder(T);

    printf("\n---非递归算法-----\n");
    printf("PreOrderNonrecursive1()：");PreOrderNonrecursive1(T);printf("\n");
    printf("PostOrderNonrecursive1()：");PostOrderNonrecursive1(T);printf("\n");

    printf("PreOrderNonrecursive2()：");PreOrderNonrecursive2(T);printf("\n");
    printf("InOrderNonrecursive2_1()：");InOrderNonrecursive2_1(T);printf("\n");
    printf("InOrderNonrecursive2_2()：");InOrderNonrecursive2_2(T);printf("\n");

    printf("PreOrderNonrecursive3()：");PreOrderNonrecursive3(T);printf("\n");
    printf("InOrderNonrecursive3()：");InOrderNonrecursive3(T);printf("\n");
    printf("PostOrderNonrecursive3()：");PostOrderNonrecursive3(T);printf("\n");

    printf("---层次遍历---\n");
    LevelOrder(T);printf("\n");



    return 0;
}

// 先序遍历创建二叉树
Status PreCreate(BiTree *pT) {
    char ch;
    scanf("%c", &ch);
    if ('#' == ch ) *pT=NULL;
    else {
        *pT = (BiTNode *)malloc(sizeof(BiTNode));
        if (!*pT) exit(OVERFLOW);
        (*pT)->data = ch;
        PreCreate( &(*pT)->lchild );
        PreCreate( &(*pT)->rchild );
    }
    return OK;
}
// 先序遍历二叉树
void PreOrder(BiTree T) { // - 递归
    if (!T) return ;
    visit(T->data);
    PreOrder(T->lchild);
    PreOrder(T->rchild);
}
// 中序遍历二叉树
void InOrder(BiTree T) { // - 递归
    if (!T) return ;
    InOrder(T->lchild);
    visit(T->data);
    InOrder(T->rchild);
}
// 后序遍历二叉树
void PostOrder(BiTree T) { // - 递归
    if (!T) return ;
    PostOrder(T->lchild);
    PostOrder(T->rchild);
    visit(T->data);
}
// 层次遍历DFS
void LevelOrder(BiTree T) {
    BiTNode *queue[maxSize]; int front,rear;
    BiTNode *p;

    if (!T) return;
    front=rear=0;
    queue[rear] = T;rear = (rear+1)%maxSize;
    while (front!=rear) {
        p = queue[front];front=(front+1)%maxSize;
        visit(p->data);
        if (p->lchild) {
            queue[rear] = p->lchild;
            rear = (rear+1)%maxSize;
        }
        if (p->rchild) {
            queue[rear] = p->rchild;
            rear = (rear+1)%maxSize;
        }
    }
}

// 求二叉树深
int BiTreeDepth(BiTree T) {
    int l,r,tmp;

    if (!T) return 0;
    else if (!T->lchild && !T->rchild) return 1;
    else {
        l = BiTreeDepth(T->lchild);
        r = BiTreeDepth(T->rchild);
        tmp = l>=r?l:r;
        return 1+tmp;
    }
}

// 遍历 - 非递归 
// - 思路一：根据访问次序来入栈并输出
// -- 缺点：没有模拟遍历的实质--对一个结点的三次的访问
void PreOrderNonrecursive1(BiTree T) { //先序遍历
    /*方法原理：
        1. 先序：根左右
        2. 访问根，然后把右、左入栈（先入栈后输出，所以将右子树先入栈）
    */
    BiTNode *p;
    BiTNode *Stack[maxSize]; //自己实现栈，适合做题
    int top=-1; //top指向当前元素

    if (!T) return ;
    Stack[++top] = T; //根结点入栈
    while (top!=-1) {
        p = Stack[top--];
        visit(p->data);
        // 右孩子先入栈，先入栈后输出
        if (p->rchild) Stack[++top]=p->rchild; //把右孩子入栈
        if (p->lchild) Stack[++top]=p->lchild; //把左孩子入栈
    }
}
void PostOrderNonrecursive1(BiTree T) {
    /* 方法原理：
    思路：
        1. 先序：根左右
        2. 后序：左右根 --> 逆后序：根右左
        3. 比较【先序】和【逆后序】：发现根是一样的，知识左右换了一下
    结论：
        1. 与PreOrderNonrecursive1方法类似，只是先将左孩子先入栈（先入栈后输出），得到逆后序序列
        2. 将逆后序数列倒过来输出
    */
    BiTNode *p;
    BiTNode *Stack[maxSize]; int top1=-1;
    BiTNode *InPostOrderStack[maxSize]; int top2=-1;
    Stack[++top1] = T;
    while (top1!=-1) {
        p = Stack[top1--];
        InPostOrderStack[++top2]=p;
        if (p->lchild) Stack[++top1]=p->lchild;
        if (p->rchild) Stack[++top1]=p->rchild;
    }
    while (top2!=-1) {
        p = InPostOrderStack[top2--];
        visit(p->data);
    }
}

// - 思路二：模拟访问过程
// -- 步骤：走到最左下角，直到走不通-->退回去，往右走一步-->往复
// -- 缺点：只模拟出前两次访问，没有模拟出最后一次访问-->所以该方法不能实现后序遍历
void PreOrderNonrecursive2(BiTree T) { //先序遍历
    BiTNode *Stack[maxSize];int top=-1; //SqStack S;
    BiTNode *p;

    Stack[++top]=T;//Push(&S, T);
    while (top!=-1) { //栈不为空
        //向左走到尽头
        while (p=Stack[top]) {
            visit(p->data);
            Stack[++top]=p->lchild;
        }
        --top; //上一步多将一个NULL放入栈了，删除它
        if (top!=-1) { //退一步，并向右走一步
            p=Stack[top--];
            Stack[++top]=p->rchild;
        }
    }
}
Status InOrderNonrecursive2_1(BiTree T) { //中序遍历
    BiTNode *p;
    BiTNode *Stack[maxSize];int top=-1; //创建栈

    Stack[++top]=T; //根指针进栈
    while (top!=-1) {
        while (p=Stack[top]) Stack[++top] = p->lchild;//向左走到尽头
        --top;//空指针出栈
        if (top!=-1) {//访问结点，向右一步
            p=Stack[top--];
            visit(p->data);
            Stack[++top]=p->rchild;
        }
    }
    return OK;
}
Status InOrderNonrecursive2_2(BiTree T) { //中序遍历
    BiTNode *p;
    BiTNode *Stack[maxSize];int top=-1; //创建栈

    p=T;
    while (p || top!=-1 ) {
        if (p) { //根指针进栈，遍历左子树
            Stack[++top]=p;
            p=p->lchild;
        } else { //根指针退栈，访问根结点，遍历右子树
            p=Stack[top--];
            visit(p->data);
            p=p->rchild;
        }
    }
    return OK;
}
// - 思路三：使用标识符mark来记录已经第几次访问该结点
// -- 优点：该方法可以模拟出遍历的实质--同一个结点将会三次访问 --> 可以完成三种遍历的任何一种
// -- 缺点：构造了一个结构体，开销大
void PreOrderNonrecursive3(BiTree T) { //先序遍历
    PMType pm;
    PMType stack[maxSize];int top=-1; //栈

    pm.mark=ZERO;pm.ptr=T;stack[++top]=pm; //根结点入栈
    while (top!=-1) { //栈不空
        pm = stack[top--]; //取出栈顶
        switch (pm.mark) {
        case ZERO: //第一次访问该结点
            visit(pm.ptr->data);
            pm.mark=ONE;stack[++top]=pm; //修改mark域，再放入栈
            if (pm.ptr->lchild) {//往左走
                pm.mark = ZERO;pm.ptr=pm.ptr->lchild;
                stack[++top] = pm;
            }
            break;
        case ONE: //左子树处理返回，第二次访问
            pm.mark=TWO;stack[++top]=pm; //修改mark域，再放入栈
            if (pm.ptr->rchild) { //往右走
                pm.mark=ZERO;pm.ptr=pm.ptr->rchild;
                stack[++top]=pm;
            }
            break;
        case TWO: //右子树处理访问，第三次访问
            break; //空操作
        }
    }
}
void InOrderNonrecursive3(BiTree T) { //中序遍历
    PMType pm;
    PMType stack[maxSize];int top=-1; //栈

    pm.mark=ZERO;pm.ptr=T;stack[++top]=pm; //根结点入栈
    while (top!=-1) { //栈不空
        pm = stack[top--]; //取出栈顶
        switch (pm.mark) {
        case ZERO: //第一次访问该结点
            pm.mark=ONE;stack[++top]=pm; //修改mark域，再放入栈
            if (pm.ptr->lchild) {//往左走
                pm.mark = ZERO;pm.ptr=pm.ptr->lchild;
                stack[++top] = pm;
            }
            break;
        case ONE: //左子树处理返回，第二次访问
            visit(pm.ptr->data);
            pm.mark=TWO;stack[++top]=pm; //修改mark域，再放入栈
            if (pm.ptr->rchild) { //往右走
                pm.mark=ZERO;pm.ptr=pm.ptr->rchild;
                stack[++top]=pm;
            }
            break;
        case TWO: //右子树处理访问，第三次访问
            break; //空操作
        }
    }
}
void PostOrderNonrecursive3(BiTree T) { //后序遍历
    PMType pm;
    PMType stack[maxSize];int top=-1; //栈

    pm.mark=ZERO;pm.ptr=T;stack[++top]=pm; //根结点入栈
    while (top!=-1) {
        pm = stack[top--];
        switch (pm.mark) {
        case ZERO: //刚刚访问此结点
            pm.mark=ONE;stack[++top]=pm; //修改mark域
            if (pm.ptr->lchild) {
                pm.mark = ZERO;pm.ptr = pm.ptr->lchild;
                stack[++top] = pm; //访问左子树
            }
            break;
        case ONE: //左子树处理返回
            pm.mark=TWO;stack[++top]=pm; //修改mark域
            if (pm.ptr->rchild) {
                pm.mark = ZERO;pm.ptr=pm.ptr->rchild;
                stack[++top] = pm; //访问右子树
            }
            break;
        case TWO: //右子树处理返回
            visit(pm.ptr->data);
        }
    }
}