内部排序

性能 分析
平均时间复杂度 特殊：基数排序O(d(n+rd))；d为关键字位数，r为一位的关键字取值范围，n为数量
“快些以nlog2n的速度归队”：快（快速排序）、些（希尔排序）、归（归并排序）、队（堆排序）
最坏时间复杂度 1. 快速排序的时间复杂度为O(n2)
2. 其他都和平均情况相等
最好时间复杂度 1. 直接插容易插变成O(n)，起泡起的好变成O(n)
2. “容易插”、“起的好”都是指初始序列已经有序
空间复杂度 1. 快速排序O(log2n)
2. 归并排序O(n)
3. 基数排序O(rd)
4. 其他都是O(1)
稳定性 【助记】考研复习痛苦啊，心情不稳定（不稳定的算法），快（快速排序）些（希尔排序）选（简单选择排序）一堆（堆排序）好友来聊天吧
。这4种不是稳定的，其他自然都是稳定的
排序原理 1. 经过一趟排序，就能保证一个元素到达最终位置：起泡、快速（交换类的两种），简单选择、堆（选择类的两种）
2. 排序方法的元素比较次数和原始序列无关：简单选择排序、折半插入排序
3. 排序方法的排序趟数和原始序列有关：交换类的排序
4. 比较类的算法，在最坏的情况下能达到最好的时间复杂度为O(nlog2n)
其他 简单普通的排序方法的升级版的平均复杂度都为O(nlog2n)，最坏的情况都是和没改进的时候一样O(n^2)，除了堆排序
排序方法 说明 代码与重点
直接插入排序 排序 - 图1 排序 - 图2
折半插入排序 用折半查找法定位每次最值的插入位置 排序 - 图3
希尔排序 用增量来划分子序列，在每个子序列中进行插入排序
排序 - 图4		 【增量选取规则】①增量序列的最后一个值一定取1；②增量序列中的值应尽量没有除1之外的公因子
【时间复杂度】与增量选取有关
1. 每次将增量除以2并向下取整排序 - 图5#card=math&code=O%28n%5E2%29&id=SvBB8)；
2. 增量排序 - 图6、65、33、17、9、5、3、1：排序 - 图7#card=math&code=O%28n%5E%7B1.5%7D%29&id=G6LDV)排序 - 图8
冒泡排序 排序 - 图9 排序 - 图10
简单选择排序 排序 - 图11 排序 - 图12
堆排序 用堆来选择最值排序 - 图13 排序 - 图14
二路归并排序 排序 - 图15 排序 - 图16
基数排序 排序 - 图17

外部排序

内部排序的归并算法 外部排序的归并算法 相同点
子序列存在内存中 子序列在外存中（文件中） 思想一样，都是从小单元归并到单元
外部排序归并操作法 涉及的内容 说明 文件内容
文件中存有n个数，但内存大小只能存放m个数 15 19 04 83 12 27 11 25 16 34 26 07 10 90 06
第一阶段 置换-选择排序 将文件中的数据处理成多个有序子序列 【第一种结果】每个子序列长度相同：4 12 15 19 83 | 11 16 25 27 34 | 6 7 10 26 90
【第二种结果】每个子序列长度不同：4 12 15 19 25 27 34 83 | 7 10 11 16 26 90 | 6
可选步骤 最佳归并树（生成哈夫曼树的方法） 计算最优的归并方案 文件中生成了3个有序子序列，但长度都不相同。在进行二路归并时，策略就有很多：①12先归并,再和3 ②13先归并,再和2 ③23先归并, 再和1
归并方案很多，如何取最优的归并方案呢？
第二阶段 败者树（选择每个归并段的最小值） 对文件中的多个有序子序列进行归并操作 4 6 7 10 11 12 15 16 19 25 26 27 34 83 90
说明
置换-选择排序 排序 - 图18
最佳归并树 【I/O次数计算方法I/O次数=带权路径长度*2】 I/O次数=2*WPL=446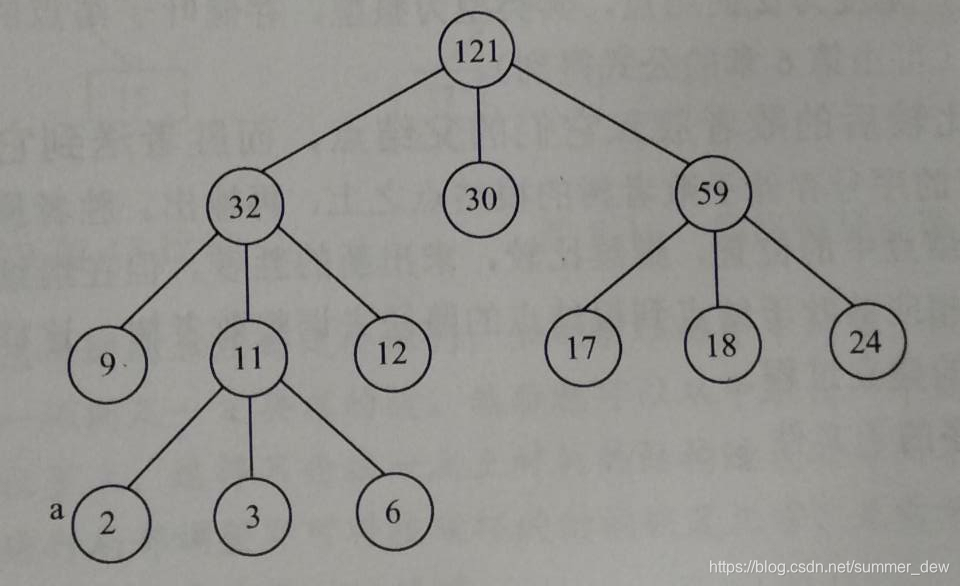
排序 - 图19
败者树 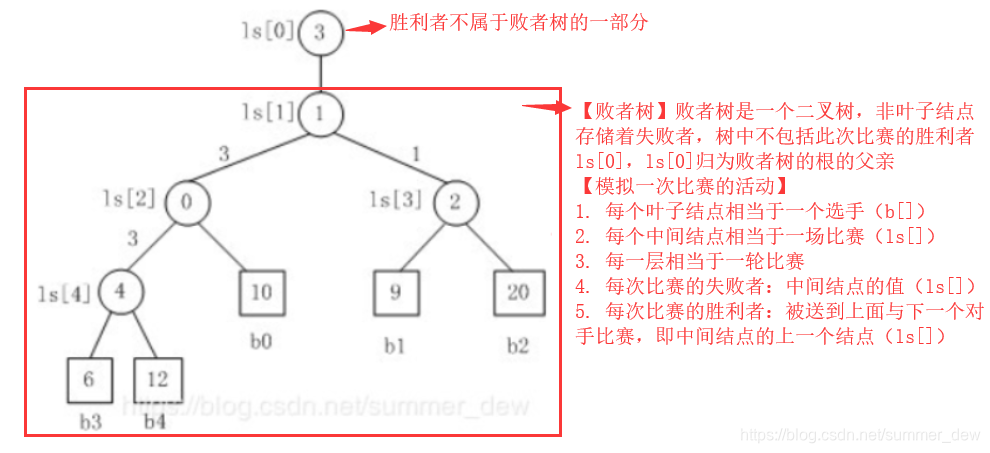排序 - 图20

【空间复杂度】O(1)
【时间复杂度】

步骤 说明 时间复杂度 I/O操作
【第一阶段】初始归并段的生成 置换选择排序 选择最值那一步的时间复杂度要根据考试要求选择算法而定 所有记录都要进行两次I/O操作
【可选阶段】最佳归并树 生成哈夫曼树
【第二阶段】选择最值 用败者树选择最值 1. 【败者树建树】O(klog2k)
2. k路归并的败者树高度⌈log2k⌉+1，从k个记录中选择最值需要进行⌈log2k⌉此比较，即时间复杂度是O(log2k)
【第二阶段】归并 归并 m个初始归并段进行k路归并，归并的趟数⌈logkm⌉ 每次归并，所有记录都要进行两次I/O操作