将树（孩子链表CTree）打印成树状（凹入表形式）（严蔚敏《数据结构》6.72）

题目来源：严蔚敏《数据结构》C语言版本习题册 6.72

【题目】6.72
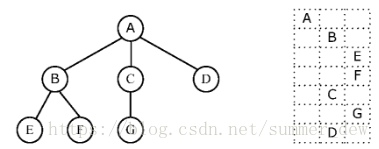
假设树上每个结点所含的数据元素为一个字母，并且以孩子链表为树的存储结构，试写一个按凹入表方式打印一棵树的算法。例如：左下所示树印为右下形状。

【思路】

1. 观察题目输出的序列ABEFCGD
2. 此为树的先根遍历–>对应为二叉树存储的先序遍历
3. 前面的空格是该结点所在的层数

【答案】

/*-------------------------
 |6.72 将树打印成树状     |
 -------------------------*/
void PrintAsTree(CTree T, int index, int i) {
    /*思路
        1. 观察题目输出的序列ABEFCGD
        2. 此为树的先根遍历–>对应为二叉树存储的先序遍历
        3. 前面的空格是该结点所在的层数
    */
    CNode *p;
    int cnt;
    //输出空格
    for (cnt=1; cnt<i; cnt++) printf(" ");
    //输出元素
    visit(T.nodes[index].data);printf("\n");
    //遍历它的孩子
    for(p=T.nodes[index].firstchild; p; p=p->next)
        PrintAsTree(T, p->index, i+1);
}

【完整代码】

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#ifndef BASE
#define BASE
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int bool;
#endif

#define TElemType char
void visit(TElemType e) {
    printf("%c ", e);
}
#define MAX_TREE_SIZE 100
#define maxSize 50

typedef struct CNode{
    int index; //这个孩子的结点号（注意：在严书中变量名为child）
    struct CNode *next; //下一个孩子结点
}CNode, *ChildPtr; //孩子结点结构（在严书中名为CTNode）
typedef struct{
    TElemType data;
    CNode* firstchild;
}PNode; //双亲结点结构（在严书中，结构名为CTBox）
typedef struct{
    PNode nodes[MAX_TREE_SIZE];
    int n,r; //结点数 和 根结点的位置
}CTree; //树结构

// 先根遍历
void SubPreOrder(CTree T, int index) {
    CNode *child;
    visit(T.nodes[index].data);
    for (child=T.nodes[index].firstchild; child; child=child->next)
        SubPreOrder(T, child->index);
}
void PreOrder(CTree T) {
    SubPreOrder(T, T.r);
}


/*-------------------------
 |6.63 求树的深度         |
 -------------------------*/
int SubTreeDepth(CTree T, int index) { //序号为index的子树深度
    int max=-1; //孩子的最大深度
    int sd; //孩子的深度
    CNode *p;
    if (!T.nodes[index].firstchild) return 1; //没有孩子，深度为1
    for (p=T.nodes[index].firstchild; p; p=p->next) { //遍历该结点的所有孩子
        sd = SubTreeDepth(T, p->index); //求孩子的深度
        if (max<sd) max=sd;
    }
    return max+1; //孩子的最大深度+1
}
int TreeDepth(CTree T) { 
    return SubTreeDepth(T, T.r);
}

/*-------------------------
 |6.72 将树打印成树状     |
 -------------------------*/
void PrintAsTree(CTree T, int index, int i) {
    /*思路
        1. 观察题目输出的序列ABEFCGD
        2. 此为树的先根遍历–>对应为二叉树存储的先序遍历
        3. 前面的空格是该结点所在的层数
    */
    CNode *p;
    int cnt;

    //输出空格
    for (cnt=1; cnt<i; cnt++) printf(" ");
    //输出元素
    visit(T.nodes[index].data);printf("\n");
    //遍历它的孩子
    for(p=T.nodes[index].firstchild; p; p=p->next)
        PrintAsTree(T, p->index, i+1);
}

// 树的层序次序+每个结点的度 --> 创建CTree
Status CreateCTreeByLevelDegree(CTree *pT,char *levelstr, int *degree) {
    CNode *c,*sibling;
    int parent;
    int i,cnt;
    //创建结点
    for (i=0; i<strlen(levelstr); ++i) {
        //赋值
        pT->nodes[i].data = levelstr[i];
        pT->nodes[i].firstchild = NULL;
    }
    pT->n=strlen(levelstr); //个数
    pT->r=0; //根结点

    //为孩子找爸爸
    parent=0; //当前的爸爸
    i=1; //遍历孩子
    cnt=0; //已经为parent找到了cnt个孩子
    while (i<strlen(levelstr)) {
        if (degree[parent]==0 || cnt==degree[parent]) { //parent没有孩子 || parent的孩子已经全部找到
            cnt=0;
            parent++;
            continue;
        }
        cnt++; //为parent找到了一个孩子
        //创建孩子结点
        c = (CNode *)malloc(sizeof(CNode)); if (!c) exit(OVERFLOW);
        c->index = i; //孩子的编号
        c->next = NULL;
        if (cnt==1) { //第一个孩子
            pT->nodes[parent].firstchild = c;
        } else { //不是第一个孩子
            for(sibling=pT->nodes[parent].firstchild; sibling->next; sibling=sibling->next) ;
            sibling->next = c;
        }

        i++;
    }
    return TRUE;
}

int main() {
/*6.72测试数据
ABCDEFG
3 2 1 0 0 0 0
*/
    CTree T;
    char levelstr[50]; //层次遍历的序列
    int num[50]; //每个结点的度
    int i,ret;

    scanf("%s", levelstr);
    for (i=0; i<strlen(levelstr); i++) scanf("%d", &num[i]);
    CreateCTreeByLevelDegree(&T, levelstr, num);


    PreOrder(T); //先根遍历

    ret = TreeDepth(T); //6.63 树的深度
    printf("\nTreeDepth：%d\n", ret);

    PrintAsTree(T, T.r, 1);


    return 0;
}