原理

【迪杰斯特拉Dijkstra】是一种贪心思想

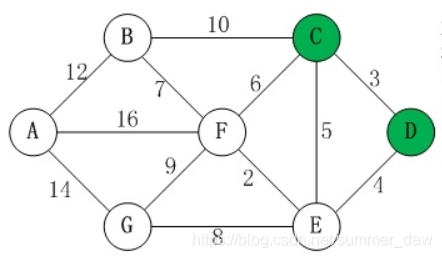
每次从子图（绿色的顶点）中找到一条通往未知顶点（白色）的最短路径（D->E）
将此路中的未知顶点E加入子图（涂绿）
【贪心思想的核心】把刚加入子图的顶点E当成中转站，考虑子图（C、D）经过中转站E到其他顶点的路会不会更近
重复以上步骤，直到子图成长为完整的图

Dijkstra（一到多） - 图1

算法中的数据结构

数组	值含义
`set[i]`	结点`i` 是否在子图中
`dist[i]`	起点v0到结点i的最短路径值为`dist[i]`
`path[i]`	起点v0与顶点i的最短路径为`v0-> .... -> path[i] -> i` ，即path[i]为该路径中i的前一个结点

path[]数组深入解释

【path[]数组的全面解释】path[]实际上就是保存了一棵树，一棵用双亲存储结构存储的树
【示例】path[v]存储的是v0->v的最短路径
【特殊值】path[v]=-1：起点到v的最短路径中，v没有前一个结点了
以下所说最短路径都是逆序，是path[v]往上找的结果

最短路径	说明
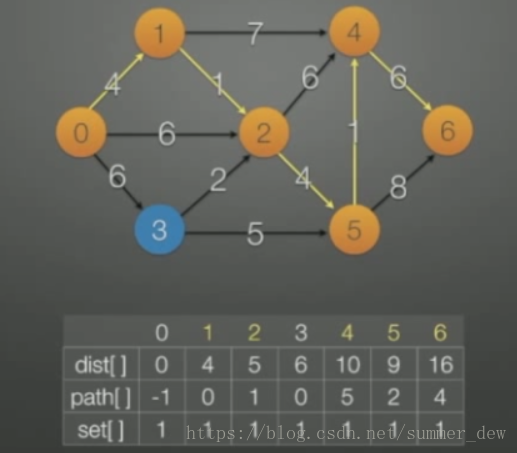
起点0到结点6的最短路径	path[6]=4，path[4]=5，path[5]=2，path[2]=1，path[1]=0，path[0]=-1停止，即0到6的最短路径为：6->4->5->2->1->0
起点0到结点5的最短路径	path[5]=2，path[2]=1，path[1]=0，path[0]=-1停止，即0到5的最短路径为：5->2->1->0
0—>4的最短路径	path[4]=5，path[5]=2，path[2]=1，path[1]=0，path[0]=-1停止，即0到6的最短路径为：4->5->2->1->0
0—>3的最短路径	path[3]=0，path[0]=-1停止，即0到3的最短路径为：3->0
0—>2的最短路径	path[2]=1，path[1]=0，path[0]=-1结束，即0到2的最短路径为：2->1->0
6. 0—>1的最短路径	path[1]=0，path[0]=-1结束，即0到1的最短路径为：1->0

Dijkstra（一到多） - 图2

求单点到其余各点的最短路径

【测试数据】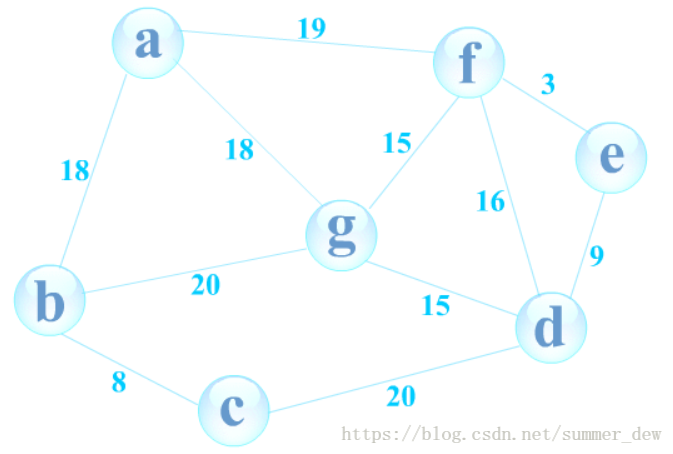
Dijkstra（一到多） - 图3
【结果】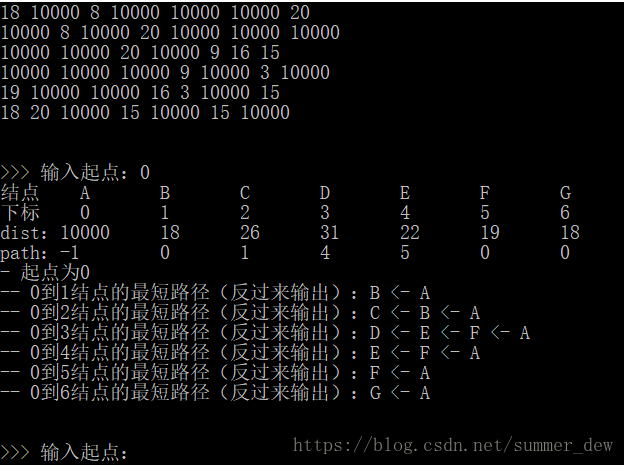
Dijkstra（一到多） - 图4

函数：单点到多点的最短路径

void Dijkstra(int n, int MGraph[][maxSize], int start, int dist[], int path[]) {
    int set[maxSize];
    int min,v;
    int i,j;
    //初始化
    for (i=0; i<n; i++) {
        dist[i]=MGraph[start][i];
        set[i]=0;
        if (MGraph[start][i]<INF)
            path[i]= start;
        else
            path[i]=-1;
    }
    set[start]=1;path[start]=-1;
    //对剩余的每个顶点进行处理
    for (i=0; i<n-1; ++i) {
        //选出与起点距离最近的点
        min=INF;
        for (j=0; j<n; j++) {
            if (set[j]==0 && dist[j]<min) {
                v=j;
                min=dist[j];
            }
        }
        set[v]=1;
        //对dist、path更新
        for (j=0; j<n; ++j) {
            if (set[j]==0 && dist[v]+MGraph[v][j]<dist[j]) {
                dist[j]=dist[v]+MGraph[v][j];
                path[j]=v;
            }
        }
    }
}

完整代码

#include<stdio.h>
#include<stdlib.h>

#define maxSize 10
#define INF 100000

void Dijkstra(int n, int MGraph[][maxSize], int start, int dist[], int path[]) {
    int set[maxSize];
    int min,v;
    int i,j;

    //初始化
    for (i=0; i<n; i++) {
        dist[i]=MGraph[start][i];
        set[i]=0;
        if (MGraph[start][i]<INF)
            path[i]= start;
        else
            path[i]=-1;
    }
    set[start]=1;path[start]=-1;

    //对剩余的每个顶点进行处理
    for (i=0; i<n-1; ++i) {
        //选出与起点距离最近的点
        min=INF;
        for (j=0; j<n; j++) {
            if (set[j]==0 && dist[j]<min) {
                v=j;
                min=dist[j];
            }
        }
        set[v]=1;

        //对dist、path更新
        for (j=0; j<n; ++j) {
            if (set[j]==0 && dist[v]+MGraph[v][j]<dist[j]) {
                dist[j]=dist[v]+MGraph[v][j];
                path[j]=v;
            }
        }
    }
}

int MGraph[maxSize][maxSize]; //邻接矩阵
char vertex[maxSize];
int main() {
/*
7
ABCDEFG
10000 18 10000 10000 10000 19 18
18 10000 8 10000 10000 10000 20
10000 8 10000 20 10000 10000 10000
10000 10000 20 10000 9 16 15
10000 10000 10000 9 10000 3 10000
19 10000 10000 16 3 10000 15
18 20 10000 15 10000 15 10000
0
*/
    int n;
    int i,j;
    char tmp[maxSize+5];
    int start,end;
    int dist[maxSize],path[maxSize];

    scanf("%d", &n); //结点数
    scanf("%s", tmp); //结点信息
    for (i=0; i<n; i++)
        vertex[i] = tmp[i];
    for (i=0; i<n; i++) { //矩阵
        for (j=0; j<n; j++) {
            scanf("%d", &MGraph[i][j]);
        }
    }
    while (1) {
        printf("\n\n>>> 输入起点：");
        scanf("%d" , &start); //输入两个测试的顶点，求v->w的最短路径
        Dijkstra(n, MGraph, start, dist, path);

        printf("结点\t");
        for (i=0; i<n; i++) {
            printf("%c\t", vertex[i]);
        }
        printf("\n下标\t");
        for (i=0; i<n; i++) {
            printf("%d\t", i);
        }
        printf("\ndist：");
        for (i=0; i<n; i++) {
            printf("%d\t", dist[i]);
        }
        printf("\npath：");
        for (i=0; i<n; i++) {
            printf("%d\t", path[i]);
        }
        printf("\n- 起点为%d\n", start);
        for (end=1; end<n; end++) {
            printf("-- %d到%d结点的最短路径（反过来输出）：", start, end);
            for (i=end; path[i]!=-1; i=path[i]) {
                printf("%c <- ", vertex[i]);
            }
            printf("%c\n", vertex[i]);
        }
    }

    return 0;
}

求两点最短路径

【测试数据】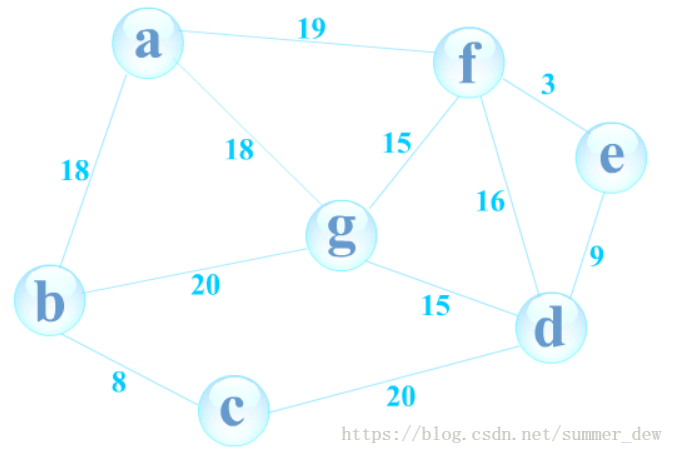
Dijkstra（一到多） - 图5
【结果】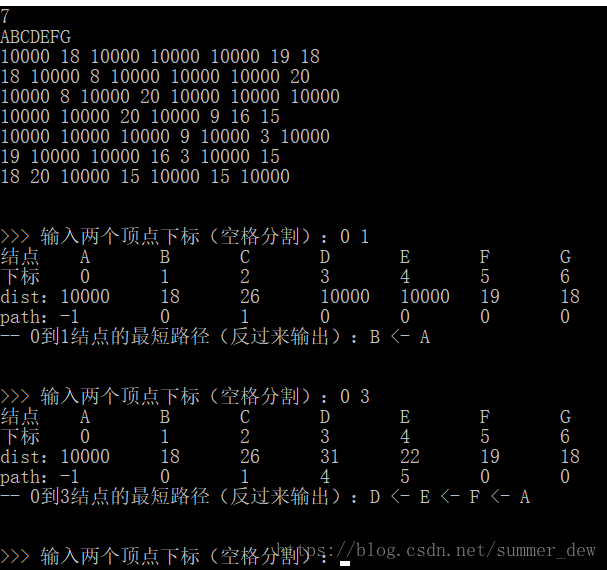
Dijkstra（一到多） - 图6

函数：两点的最短路径

void Dijkstra(int n, int MGraph[][maxSize], int start, int end, int dist[], int path[]) {
    int set[maxSize];
    int min,v;
    int i,j;

    //初始化
    for (i=0; i<n; i++) {
        dist[i]=MGraph[start][i];
        set[i]=0;
        if (MGraph[start][i]<INF)
            path[i]= start;
        else
            path[i]=-1;
    }
    set[start]=1;path[start]=-1;

    //对剩余的每个顶点进行处理
    for (i=0; i<n-1; ++i) {
        //选出与起点距离最近的点
        min=INF;
        for (j=0; j<n; j++) {
            if (set[j]==0 && dist[j]<min) {
                v=j;
                min=dist[j];
            }
        }
        set[v]=1;

        //对dist、path更新
        for (j=0; j<n; ++j) {
            if (set[j]==0 && dist[v]+MGraph[v][j]<dist[j]) {
                dist[j]=dist[v]+MGraph[v][j];
                path[j]=v;
            }
        }

        if (v==end) {
            return ; //找到了start-->end的最短路径
        }
    }
}

完整代码

#include<stdio.h>
#include<stdlib.h>

#define maxSize 10
#define INF 100000

void Dijkstra(int n, int MGraph[][maxSize], int start, int end, int dist[], int path[]) {
    int set[maxSize];
    int min,v;
    int i,j;

    //初始化
    for (i=0; i<n; i++) {
        dist[i]=MGraph[start][i];
        set[i]=0;
        if (MGraph[start][i]<INF)
            path[i]= start;
        else
            path[i]=-1;
    }
    set[start]=1;path[start]=-1;

    //对剩余的每个顶点进行处理
    for (i=0; i<n-1; ++i) {
        //选出与起点距离最近的点
        min=INF;
        for (j=0; j<n; j++) {
            if (set[j]==0 && dist[j]<min) {
                v=j;
                min=dist[j];
            }
        }
        set[v]=1;

        //对dist、path更新
        for (j=0; j<n; ++j) {
            if (set[j]==0 && dist[v]+MGraph[v][j]<dist[j]) {
                dist[j]=dist[v]+MGraph[v][j];
                path[j]=v;
            }
        }

        if (v==end) {
            return ; //找到了start-->end的最短路径
        }
    }
}

int MGraph[maxSize][maxSize]; //邻接矩阵
char vertex[maxSize];
int main() {
/*
7
ABCDEFG
10000 18 10000 10000 10000 19 18
18 10000 8 10000 10000 10000 20
10000 8 10000 20 10000 10000 10000
10000 10000 20 10000 9 16 15
10000 10000 10000 9 10000 3 10000
19 10000 10000 16 3 10000 15
18 20 10000 15 10000 15 10000
0 1
0 3
*/
    int n;
    int i,j;
    char tmp[maxSize+5];
    int start,end;
    int dist[maxSize],path[maxSize];

    scanf("%d", &n); //结点数
    scanf("%s", tmp); //结点信息
    for (i=0; i<n; i++)
        vertex[i] = tmp[i];
    for (i=0; i<n; i++) { //矩阵
        for (j=0; j<n; j++) {
            scanf("%d", &MGraph[i][j]);
        }
    }
    while (1) {
        printf("\n\n>>> 输入两个顶点下标（空格分割）：");
        scanf("%d %d" , &start,&end); //输入两个测试的顶点，求v->w的最短路径
        Dijkstra(n, MGraph, start, end, dist, path);

        printf("结点\t");
        for (i=0; i<n; i++) {
            printf("%c\t", vertex[i]);
        }
        printf("\n下标\t");
        for (i=0; i<n; i++) {
            printf("%d\t", i);
        }
        printf("\ndist：");
        for (i=0; i<n; i++) {
            printf("%d\t", dist[i]);
        }
        printf("\npath：");
        for (i=0; i<n; i++) {
            printf("%d\t", path[i]);
        }
        printf("\n-- %d到%d结点的最短路径（反过来输出）：", start, end);
        for (i=end; path[i]!=-1; i=path[i]) {
            printf("%c <- ", vertex[i]);
        }
        printf("%c\n", vertex[i]);
    }
    return 0;
}