问题

求含n个元素的集合的幂集

【注释】幂集：所有子集所组成的集合
【举例】

  1. A={1,2,3}
  2. ρ(A) = { {1,2,3}, {1,2}, {1,3}, {1}, {2,3}, {2}, {3}, ∅ }

思路

本问题可以用【分治法】来求解
从另一个角度分析问题：幂集的每个元素是一个集合，它或是空集，或含集合A中的一个元素，或含集合A中两个元素，或等于集合A

【相反】从集合A的每个元素来看，它只有两个状态：

  1. 属于幂集的元素集
  2. 不属于幂集元素集

【结论】ρ(A)的元素的过程可以看成是对集合A中每个元素进行 “选” 还是 “不选” 的过程

过程

由上，问题即是对A的每个元素进行选，还是不选的过程
由此可以画出过程树，即幂集元素在生成过程中的状态图
而最终的答案就是最下一层的叶子结点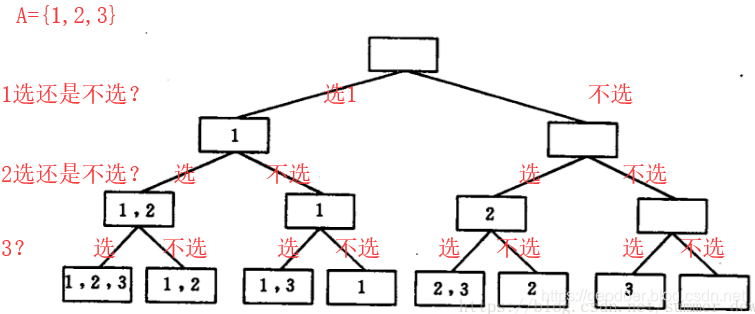
求n个元素的集合的幂集 - 图1

【解释】可以用一棵二叉树，来表示过程中幂集元素的状态变化状况

  1. 【树中的根结点】幂集元素的初始状态，为空集
  2. 【叶子结点】它的终结状态
  3. 【第i层的分支结点】已对集合A中前i-1个元素进行了”选/不选”的当前状态

【结论】求幂集元素的过程即为先序遍历这棵状态树的过程

  1. void PowerSet(int i,int n) {
  2.     // 求含n个元素的集合A的幂集ρ(A)。进入函数时已对A中前i-1个元素坐了取舍处理
  3.     // 现从第i个元素起进行取舍处理。若i>n，则求得幂集的一个元素，并输出之
  4.     // 初始调用：PowerSet(1,n);
  5.     if (i>n) 输出幂集的一个元素
  6.     else {
  7.         取第i个元素；PowerSet(i+1, n);
  8.         舍第i个元素；PowerSet(i+1, n);
  9.     }
  10. }

代码

求n个元素的集合的幂集 - 图2

  1. #include<stdio.h>
  2. #include<string.h>
  4. // 实则是输出递归树的叶子结点
  5. int P(char *str, int n, int index) {
  6.     static char tmp[100];
  7.     int case1=0,case2=0;
  9.     if (n==-1) { //输出叶子结点
  10.         tmp[index] = '\0';
  11.         printf("%s\n", tmp);
  12.         return 1;
  13.     }
  14.     if (n>=0) { //考虑情况
  15.         // 选n
  16.         tmp[index] = str[n];
  17.         case1 = P(str, n-1, index+1);
  18.         // 不选n
  19.         case2 = P(str, n-1, index);
  20.     }
  21.     return case1+case2;
  22. }
  24. int main() {
  25.     char tmp[50];
  26.     int cnt;
  27.     printf("输入字符串:\n>>> ");
  28.     scanf("%s", tmp);
  29.     cnt = P(tmp, strlen(tmp)-1, 0);
  30.     printf("共有%d情况", cnt);
  31.     return 0;
  32. }

拓展

图中状态变化树是一棵满二叉树：树中每个叶子结点的状态都是求解过程中可能出现的状态（即问题的解）。
【然而】很多问题用回溯和试探求解时，描述求解过程的状态树不是一棵满的多叉树

【非满多叉树】不是满的多叉树：当试探过程中出现的状态和问题所求解产生矛盾时，不再继续试探下去，这时出现的叶子结点不是问题的解的终结状态
此类问题的求解过程可看成是在约束条件下进行先序（根）遍历，并在遍历过程中剪去那些不满足条件的分支
【例子】四皇后问题