原理
【Floyd算法】用动态规划的思想求任意两点之间的最短路径
【评价】时间复杂度#card=math&code=O%28n%5E3%29&id=rvoye),空间复杂度
#card=math&code=O%28n%5E2%29&id=DYSEn),但形式上比Dijkstra简单些,也容易理解
【基本思想】以二维数组D[v][w]保存v->w的最短路径长度
- 【初始状态】D[v][w] —> 没有中间点,v直接走到w的距离
- 【分别考虑所有结点u】把u看成中转站,检查v->u->w(即D[v][u]+D[u][w])是否比v->w(即D[v][w])小,如果小就更新D[v][w]的值
【当然】我们还需要一个path[v][w]的二维数组来保存路径(path[][]详细解释请看下文)
【主要公式】
// D[v][w]存储v->w的最短路径长度// v->w中间可能经过很多点if (D[v][u] + D[u][w] < D[v][w]) { // v->u->w的长度 < 当前v->w的长度D[v][w] = D[v][u] + D[u][v]; //那么最短路径D[v][w]即是 v->u->w的距离path[i][j] = v; //i->j的路径上,有中转站v}
【算法示例】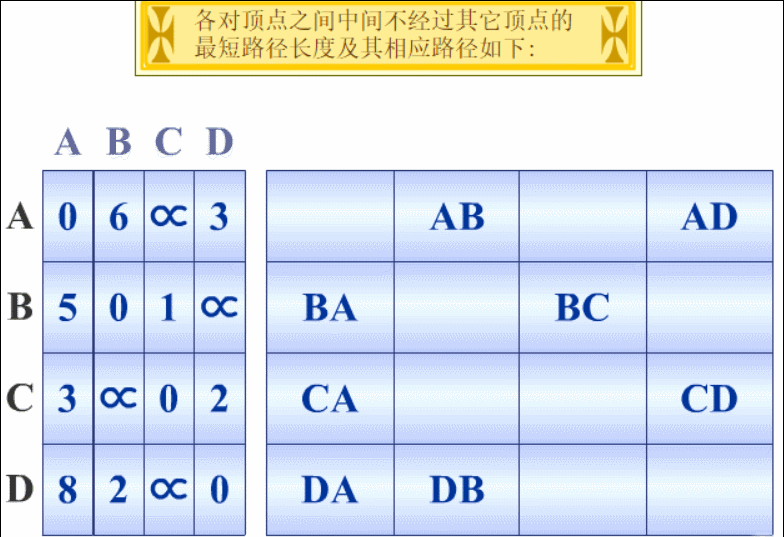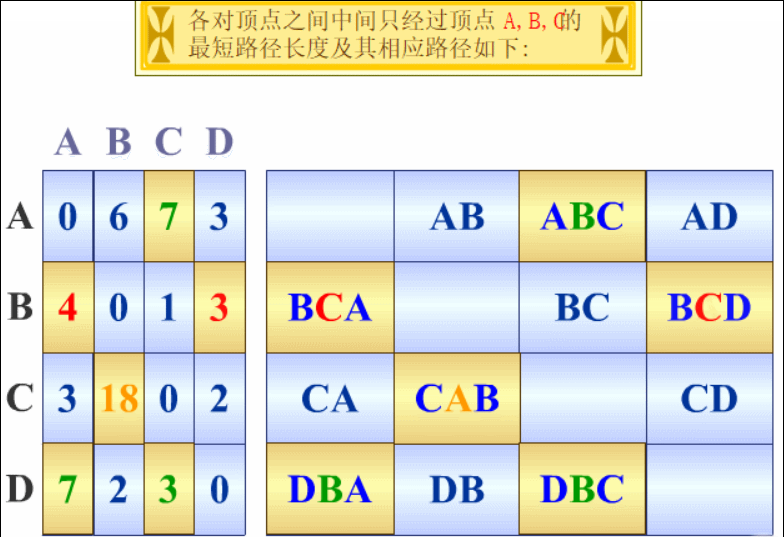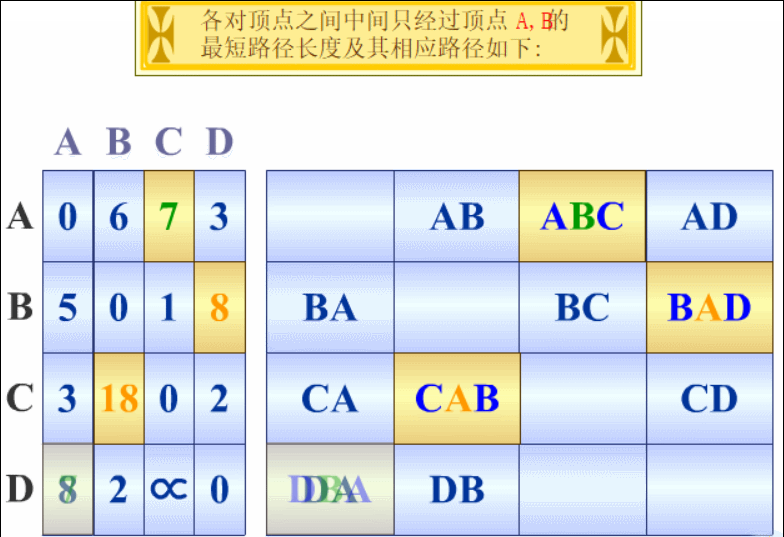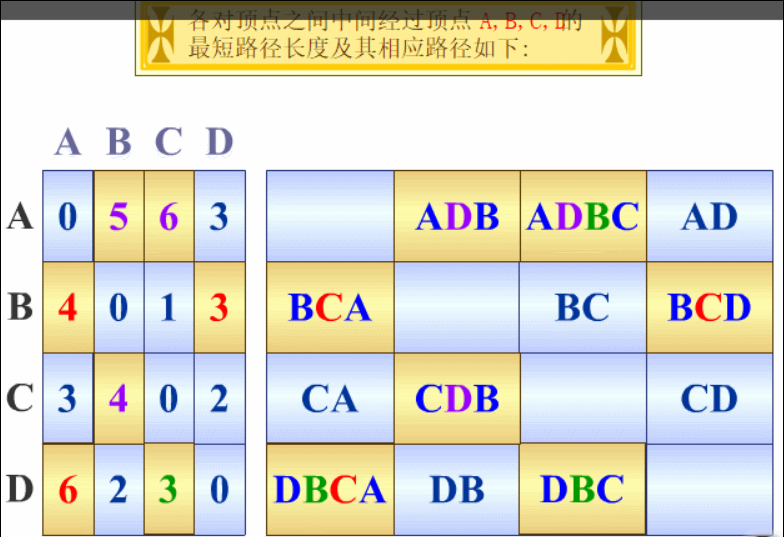
核心代码
void PrintPath(int u, int v, int path[][maxSize]) {int mid;if (path[u][v]==-1) {//直接输出,没有中间点printf("<%c,%c> ", vertexs[u], vertexs[v]);} else { //有中间点mid = path[u][v];PrintPath(u, mid, path);PrintPath(mid, v, path);}}void Floyd(int n, int MGraph[][maxSize], int path[][maxSize]) {int i,j,v;int A[maxSize][maxSize]; //最短路径//初始化:A-1没有考虑中间节点for (i=0; i<n; ++i) {for (j=0; j<n; j++) {A[i][j] = MGraph[i][j];path[i][j] = -1;}}//循环考虑中间节点for (v=0; v<n; ++v) {for (i=0; i<n; ++i) {for (j=0; j<n; ++j) {if (A[i][j]>A[i][v]+A[v][j]) {A[i][j] = A[i][v] + A[v][j];path[i][j] = v;}}}}}
代码
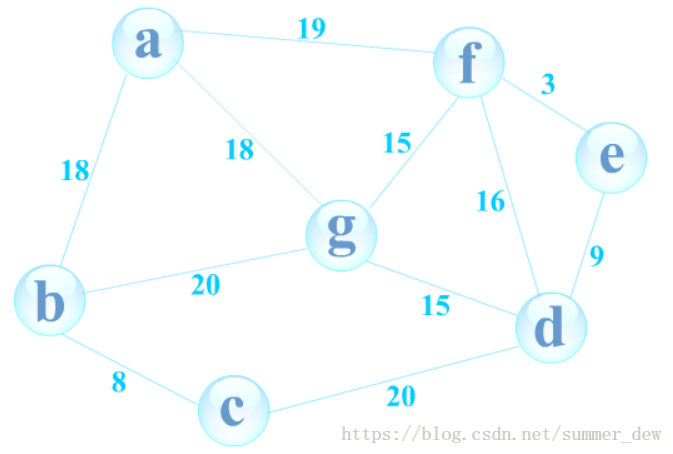
| 测试数据 | 结果 | 0->3的最短路径 |
|---|---|---|
 |
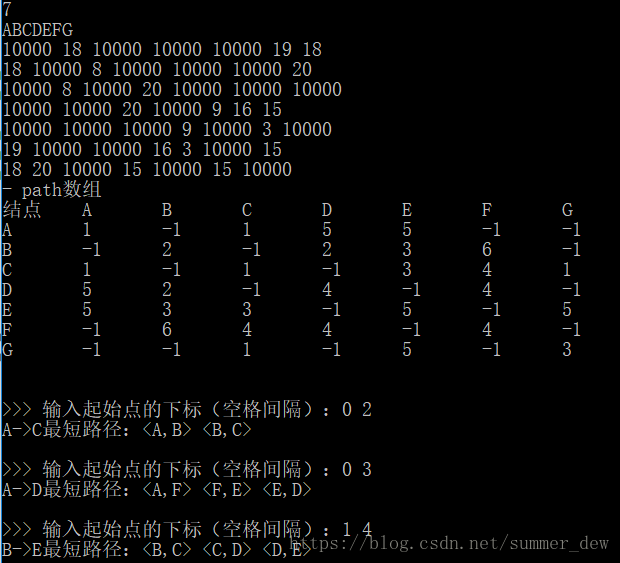 |
0到3的最短路径为0->5->4->3即 A->F->E->D |
path[][]数组解释
| 结点 | A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| A | 0 | 1 | -1 | 1 | 5 | 5 | -1 | -1 |
| B | 1 | -1 | -1 | 2 | -1 | 2 | 3 | 6 |
| C | 2 | 1 | -1 | 1 | -1 | 3 | 4 | 1 |
| D | 3 | 5 | 2 | -1 | 4 | -1 | 4 | -1 |
| E | 4 | 5 | 3 | 3 | -1 | 5 | -1 | 5 |
| F | 5 | -1 | 6 | 4 | 4 | -1 | 4 | -1 |
| G | 6 | -1 | -1 | 1 | -1 | 5 | -1 | 3 |
【path[u][v]的值】u->v的最短路径中,有中转站path[u][v]
【特殊值】path[u][v]=-1:表示u到v之间没有中间节点—>u到v的最短路径即是边u->v
【求法】求0到3的最短路径
path[0][5]=5 --> 0到3的路上有中转站5,即0->5->3- 【0->5->3前半段】
path[0][5]=1 --> 0到5的路上没有中转站了,前半段即0->5 - 【0->5->3后半段】
path[5][3]=4 --> 5到3的路上有中转站4,后半段5->4->3- 【5->4->3前半段】
path[5][4]=-1 --> 没有中转站了,即5->4 - 【5->4->3后半段】
path[4][3]=-1 --> 没有中转站,即4->3
- 【5->4->3前半段】
【综上】0到3的最短路径为0->5->4->3,即A->F->E->D
完整代码
#include<stdio.h>#include<stdlib.h>#define maxSize 10#define INF 100int MGraph[maxSize][maxSize]; //邻接矩阵char vertexs[maxSize]; //结点信息void PrintPath(int u, int v, int path[][maxSize]) {int mid;if (path[u][v]==-1) {//直接输出,没有中间点printf("<%c,%c> ", vertexs[u], vertexs[v]);} else { //有中间点mid = path[u][v];PrintPath(u, mid, path);PrintPath(mid, v, path);}}void Floyd(int n, int MGraph[][maxSize], int path[][maxSize]) {int i,j,v;int A[maxSize][maxSize]; //最短路径//初始化:A-1没有考虑中间节点for (i=0; i<n; ++i) {for (j=0; j<n; j++) {A[i][j] = MGraph[i][j];path[i][j] = -1;}}//循环考虑中间节点for (v=0; v<n; ++v) {for (i=0; i<n; ++i) {for (j=0; j<n; ++j) {if (A[i][j]>A[i][v]+A[v][j]) {A[i][j] = A[i][v] + A[v][j];path[i][j] = v;}}}}}int main() {/*7ABCDEFG10000 18 10000 10000 10000 19 1818 10000 8 10000 10000 10000 2010000 8 10000 20 10000 10000 1000010000 10000 20 10000 9 16 1510000 10000 10000 9 10000 3 1000019 10000 10000 16 3 10000 1518 20 10000 15 10000 15 100000 20 30 41 64 63 6*/int n;int i,j;char tmp[maxSize+5];int path[maxSize][maxSize];int start,end;scanf("%d", &n); //结点数scanf("%s", tmp); //结点信息for (i=0; i<n; i++)vertexs[i] = tmp[i];for (i=0; i<n; i++) { //矩阵for (j=0; j<n; j++) {scanf("%d", &MGraph[i][j]);}}Floyd(n, MGraph, path);//打印path数组printf("- path数组\n");printf("结点");for (i=0; i<n; i++) {printf("\t%c", vertexs[i]);}printf("\n");for (i=0; i<n; i++) {printf("%c\t", vertexs[i]);for (j=0; j<n; j++) {printf("%d\t", path[i][j]);}printf("\n");}//输出最短路径while (1) {printf("\n\n>>> 输入起始点的下标(空格间隔):");scanf("%d %d" , &start, &end); //输入两个测试的顶点,求v->w的最短路径printf("%c->%c最短路径:", vertexs[start], vertexs[end]);PrintPath(start, end, path);}return 0;}

