相关链接

  1. Kosaraju算法：https://blog.csdn.net/summer_dew/article/details/83047190

背景

【无向图】如果从s到t存在一条路径，那么我们知道从t到s也存在一条路径
【有向无环图（DAG）】如果从s到t存在一条路径，那么我们知道从t到s不存在有向路径
【问题】但是，对于一般的有向图，知道t由s可达并没有给出s是否由t可达的信息
【强连通分量的提出】为了理解有向图的结构，我们考虑强连通性（strong connectivity），它具有我们寻求的对称性。如果s和t是强连通的（顶点相互可达）—>那么根据定义，t和s也是强连通的
【如何判断有向图是不是强连通】暴力判断：判断任意两个顶点s，t，看从s是否可以到t，从t是否可以到s。这个算法易于描述和实现，但需要代价很大
【现代算法设计的胜利】现代算法设计能在线性时间内找出任何图的强分量，它要比蛮力算法快V倍。对于100个顶点，这些算法将比蛮力算法快100倍；对于1000个顶点，这些算法比蛮力算法块1000倍；对于设计数十亿顶点的问题也可以解决。

有向图的强连通分量

【强连通(strongly connected)】在有向图中，从我这可以走到你那，从你那能够走到我这—>我们俩强连通
【强连通图】有向图G，任意两个顶点都强连通—>G是强连通图
【非强连通图】有向图G，存在两个顶点不能够互相走通—>非强连通图
【强连通分量】在非强连通图中，顶点最多最大的强连通图—>极大强连通子图—>强连通分量

【举例】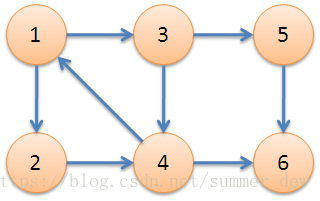
有向图的强连通分量 - 图1
连通分量

  1. {1,2,3,4}
  2. {5}
  3. {6}

【求强连通分量】

  1. Kosaraju算法：O(N+M)
  2. Tarjan算法：O(N+M)
  3. Gabow算法