其他相关链接：

  1. 最小生成树问题
  2. 最小生成树Prim算法C语言实现

  3. 最小生成森林Prim算法C语言实现

    思想

  4. 从某个顶点开始（不要把它看成一个单独的顶点，把它看成只有一个结点的子生成树）

  5. 在第一步的生成树的相邻边中，选一条最小的边，将最小的边和边的另一个结点并入子生成树中（生成树就长大了一点）
  6. 继续，直到所有的顶点都被并入了生成树

步骤

  1. 取图中任意一个顶点 v 作为生成树的根，之后往生成树上添加新的顶点 w
  2. 在添加的顶点 w 和已经在生成树上的顶点v 之间必定存在一条边，
  3. 并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小。
  4. 之后继续往生成树上添加顶点，直至生成树上含有 n-1 个顶点为止。

性能

O(n^2)，适合稠密图（边多的图）
另一个【克鲁斯卡尔算法】O(eloge)：适合稀疏图（边少的图）
博客：https://blog.csdn.net/summer_dew/article/details/81660723

举例

  1. 蓝色的顶点：还未考虑的顶点
  2. 黄色的顶点：已经考虑完的顶点
  3. 蓝色的线：未考虑的边
  4. 紫色的线：考虑范围内的边
  5. 红色的线：生成树的边（最短的边）

普利姆算法Prim（最小生成树） - 图1

将a纳入考虑的顶点，变成黄色
第一步：考虑黄色顶点【a】

  1. 考虑与a相连的所有边（紫色的边），取出最短的边：18
  2. 将最短边，纳入生成树的边（变红色）
  3. 将顶点b纳入已考虑的顶点（变黄色）

第二步：考虑黄色的顶点【a,b】

  1. 考虑与a,b相连的所有边（紫色的边），取出最短的边8
  2. 将最短边，纳入生成树的边（变红色）
  3. 将顶点c纳入已考虑的顶点（变黄色）

第三步：继续考虑黄色的顶点【a,b,c】

  1. 考虑与a,b,c相连的所有边（紫色的边），取出最短的边20
  2. 将最短边，纳入生成树的边（变红色）
  3. 将顶点d纳入已考虑的顶点（变黄色）

实现

记：

  1. 黄色的顶点，为顶点集【U】，即已落在生成树上的顶点
  2. 蓝色的顶点，为顶点集【V-U】，即尚未落在生成树上的顶点

设置一个辅助数组

  1. 下标：顶点v
  2. lowcost：记录【黄色的点们】到【v】的最短边
  3. adjvex：记录【黄色的点集】中哪一个顶点，到v最短

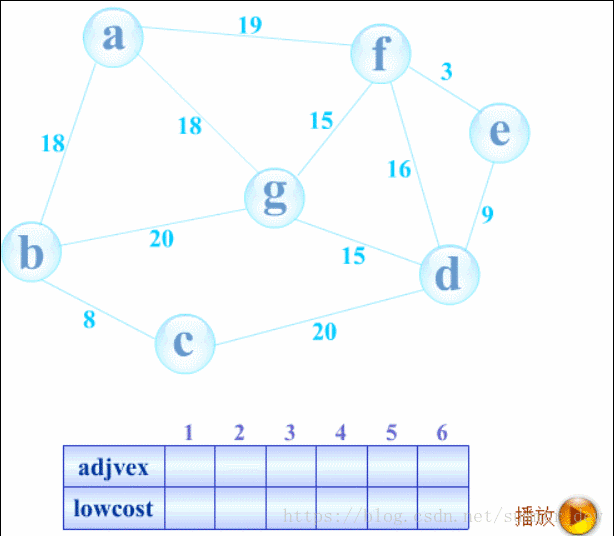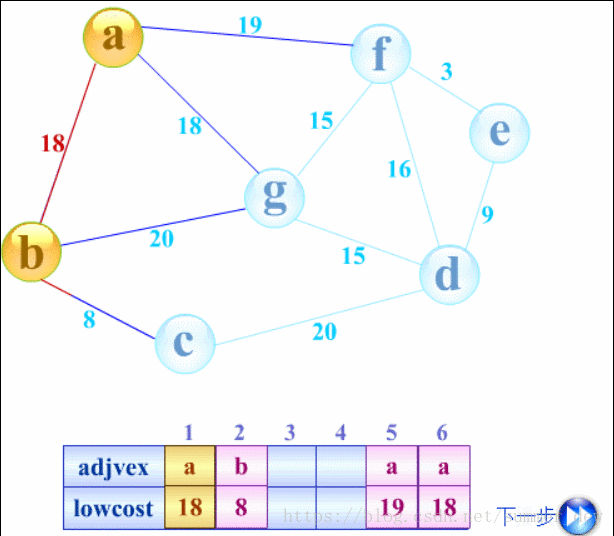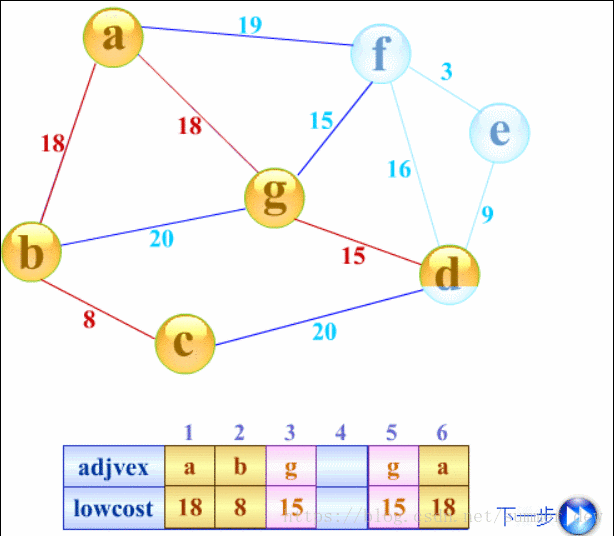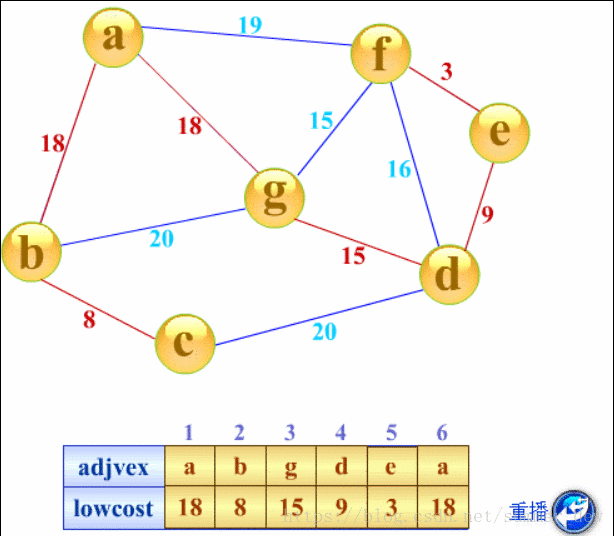
例如：下图，最初始时

  1. 下标1：表示顶点b
  2. lowcost[1]记录的是当前【黄色点集】到b的最短路径为18。
  3. 这个最短路径是从a（adjvex[1]）到b的

普利姆算法Prim（最小生成树） - 图2

  1. // 最小生成树
  2. #define INF 1000 //最大值
  3. //VRType表示边的类型
  4. VRType GetMSTSumByPrim(MGraph G, int v0) { //从v开始找最小生成树
  5.     int MST[MAX_VERTEX_NUM]; //结点i已在最小生成树里-->MST[i]=1;
  6.     VRType lowCost[MAX_VERTEX_NUM]; //最小代价
  7.     VRType sum; //生成树的代价
  9.     VRType min=INF; //当前最小的边
  10.     int minNode; //最小边的另一个顶点
  12.     int n=0; //生成树当前有几个结点
  13.     int i;
  15.     // 初始化
  16.     n=0; //生成树当前有几个结点
  17.     for (i=0; i<G.vexnum; ++i) {
  18.         lowCost[i] = G.arcs[v0][i].adj; //最小边
  19.         MST[i]=0; //访问记录
  20.     }
  21.     MST[v0]=++n; //v是生成树的第一个结点
  22.     sum=0;
  23.     // 循环考虑其他结点
  24.     while (n<G.vexnum) { //生成树中的结点数<总数
  25.         // 找lowCost里的最小值 和 对应的顶点
  26.         min = INF;
  27.         for (i=0; i<G.vexnum; i++) {
  28.             // i结点还没有并入生成树
  29.             if (MST[i]==0 && lowCost[i]<min) {
  30.                 min=lowCost[i];
  31.                 minNode=i;
  32.             }
  33.         }
  34.         // 将minNode加入生成树
  35.         sum += min;
  36.         MST[minNode]=++n;
  37.         // 更新lowCost
  38.         for (i=0; i<G.vexnum; i++) {
  39.             if (MST[i]==0 && G.arcs[minNode][i].adj<lowCost[i]) {
  40.                 lowCost[i]=G.arcs[minNode][i].adj;
  41.             }
  42.         }
  43.     }
  45.     return sum;
  46. }

完整代码

#include<stdio.h>
#include<stdlib.h>

#ifndef BASE
#define BASE
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int bool;
#endif

typedef char VertexType;//点类型
typedef int VRType; //边类型
void visit(VertexType e) {
    printf("%c", e);
}
#define maxSize 20

#define MAX_VERTEX_NUM 20
typedef enum{UDG, DG} GraphKind;
typedef struct ArcCell{
    VRType adj;
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
    VertexType vexs[MAX_VERTEX_NUM]; //顶点
    AdjMatrix arcs; //弧的信息
    int vexnum,arcnum;
    GraphKind kind;
}MGraph;

Status CreateG_MG(MGraph *pG) {
    int i,j,w;
    char tmp[maxSize];
    scanf("%d", &i); if (i<0) return ERROR;
    pG->vexnum = i;
    scanf("%d", &i); if (i<0) return ERROR;
    pG->arcnum = i;
    scanf("%s", tmp);
    for (i=0; i<pG->vexnum; i++) pG->vexs[i]=tmp[i];
    for (i=0; i<pG->vexnum; i++) {
        for (j=0; j<pG->vexnum; j++) {
            scanf("%d", &w);
            pG->arcs[i][j].adj = w;
        }
    }
    return OK;
}
// 最小生成树
#define INF 1000 //最大值
//VRType表示边的类型
VRType GetMSTSumByPrim(MGraph G, int v0) { //从v开始找最小生成树
    int MST[MAX_VERTEX_NUM]; //结点i已在最小生成树里-->MST[i]=1;
    VRType lowCost[MAX_VERTEX_NUM]; //最小代价
    VRType sum; //生成树的代价

    VRType min=INF; //当前最小的边
    int minNode; //最小边的另一个顶点

    int n=0; //生成树当前有几个结点
    int i;

    // 初始化
    n=0; //生成树当前有几个结点
    for (i=0; i<G.vexnum; ++i) {
        lowCost[i] = G.arcs[v0][i].adj; //最小边
        MST[i]=0; //访问记录
    }
    MST[v0]=++n; //v是生成树的第一个结点
    sum=0;
    // 循环考虑其他结点
    while (n<G.vexnum) { //生成树中的结点数<总数
        // 找lowCost里的最小值 和 对应的顶点
        min = INF;
        for (i=0; i<G.vexnum; i++) {
            // i结点还没有并入生成树
            if (MST[i]==0 && lowCost[i]<min) {
                min=lowCost[i];
                minNode=i;
            }
        }
        // 将minNode加入生成树
        sum += min;
        MST[minNode]=++n;
        // 更新lowCost
        for (i=0; i<G.vexnum; i++) {
            if (MST[i]==0 && G.arcs[minNode][i].adj<lowCost[i]) {
                lowCost[i]=G.arcs[minNode][i].adj;
            }
        }
    }

    return sum;
}

int main() {
/*
7
11
ABCDEFG
10000 18 10000 10000 10000 19 18
18 10000 8 10000 10000 10000 20
10000 8 10000 20 10000 10000 10000
10000 10000 20 10000 9 16 15
10000 10000 10000 9 10000 3 10000
19 10000 10000 16 3 10000 15
18 20 10000 15 10000 15 10000
*/
    MGraph G;
    int sum;

    G.kind = DG;
    CreateG_MG(&G);

    sum = GetMSTSumByPrim(G, 0);
    printf("最小生成树：%d", sum);

    return 0;
}