分段线性激活函数

简介

ReLU定义了一个明确的关闭状态，哪怕是ELU也会在-1处饱和，对于普通分类任务而言，考虑各个特征的存在与否就已经足够了，所以这些几乎函数都很适合图像分类任务，不管选用哪种，对最后的结果都只有很小的影响。
然而对于细粒度图像识别而言，仅对特征的存在与否建模并不够，因为不同的类有着相似的外观，这时候还需要对不存在的程度进行建模。这里需要用到一致连续函数和Lipschitz连续函数的概念。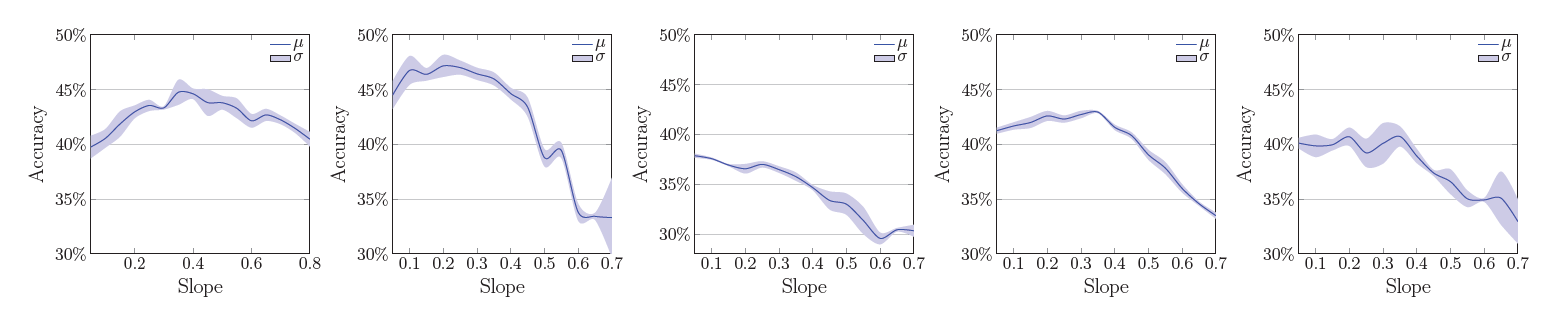

本文提出了分段线性激活函数LReLU，通过激活函数对特征的存在和缺失程度进行建模。如果当前样本存在特征，则返回大于0的值，如果不存在则返回小于0的值。这种方式可以确保所需的特征不会丢失，所有存在的特征值存在，缺失的特征都映射为0**。
这要求激活函数必须单调递增并且连续，所以本文分段定义线性激活函数，正值部分是恒等函数，负值部分是有一定斜率的线性函数。这样不但保证了所需属性，还继承了ReLU在计算效率上的优势。
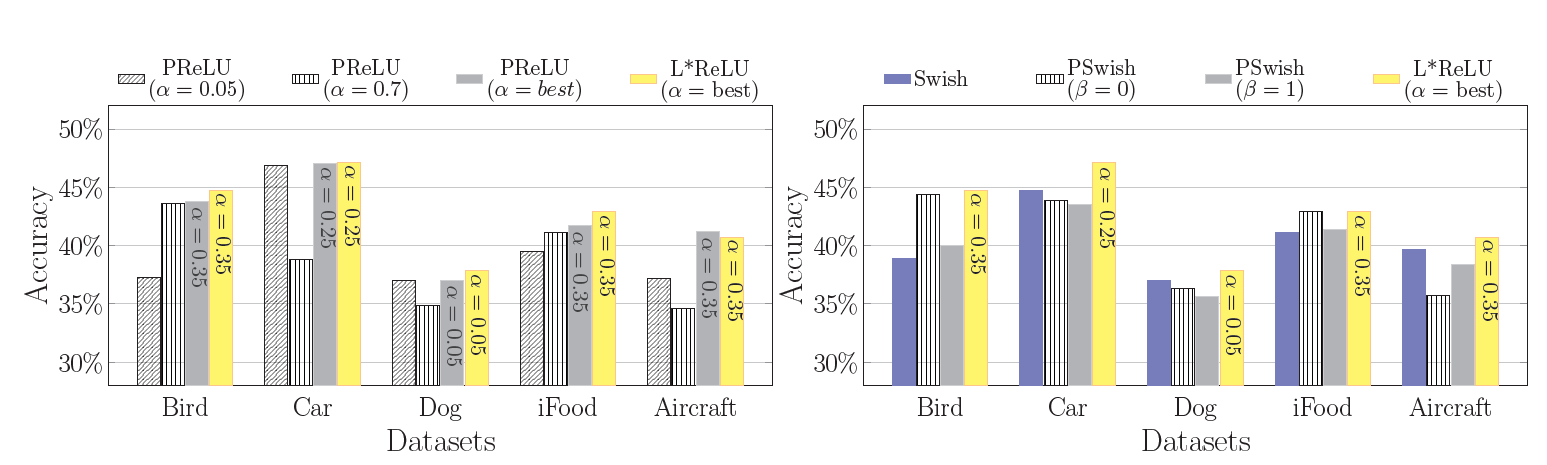
在七个数据集上进行试验，充分证明精度和基线相比的优势，同时针对不同的任务，使用不同的激活函数是很有必要的。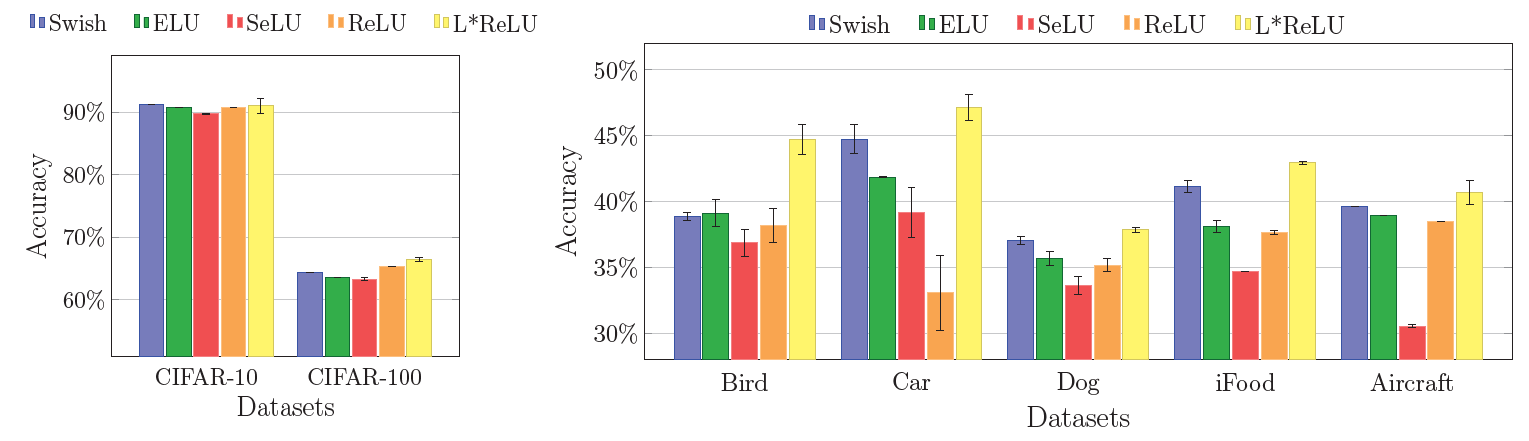

方法核心

Lipschitz常数

在一个函数中，其定义域中的任意两点的斜率都小于某个常数L，这个常数L的最小值则称为函数的Lipschitz常数，符合这个条件的函数成为Lipschitz函数。由此可以知道Lipschitz常数定义了函数在区间内的最大变化率，如果则称在定义域上的收缩映射。同时Lipschitz连续函数在指在全体实数上都是连续的，即当x无限小时，对应也为无限小。

分段线性激活函数

从之前的研究可以发现，细粒度图像分类需要一个可以表示特征存在和缺失程度进行建模，这两个方面与正负域都有关系，所以这里定义了分段函数，需要一个不饱和、单调递增、变化率有界的函数。这需要一个收缩的、无界的、连续的函数

对于有限的数据集，两个类别在输入空间最少间隔距离c，那必然存在一个具有Lipschitz常数值为c/2的函数可以正确分类所有点，不同的数据集有不同的可分离性，需要学习不同的属性函数作为斜率，可以通过Lipschitz常数来实现
于是根据数据的Lipschitz属性来选择斜率参数，为了保证输出稳定可靠的结果，可以为Lipschitz常数和斜率设定一个范围。

总结

第二水的论文，实在太坑了，酝酿半天啥都没讲。和Leaky ReLU完全一样，而且本文的Lipschitz常数还需要手动试出来，测试的结果也是拿低分辨率，只训练3个迭代来比较，完全没有说服力
不过本文提出，针对细粒度识别，使用更高的，即激活函数更接近，可能会提高精度，因为细粒度识别对特征的存在与否的程度更加敏感。本文也证明做细粒度图像分类相关研究的人并不多，完全可以继续尝试寻找更好的针对细粒度图像的激活函数