GCN算法及其dgl实现
1. DGL 框架概述
1.1 DGL框架的产生
用现有的一些框架比如 TensorFlow、Pytorch、MXNet 等实现图神经网络模型都不太方便，即使实现了，图神经网络模型的速度不够快。
为什么图神经网络模型在之前的一些框架中不容易编写呢？
因为很多图神经网络的模型，可以看作是消息传递的过程，每一个节点会发出它自己的消息，也会接受来自其它节点的消息。然后在得到所有信息之后做聚合，计算出节点新的表示。
原有的深度学习框架都是进行张量运算，但是图很多时候并不能直接表示成一个完整的张量，需要手动补零，这其实很麻烦，不高效。
1.2 DGL原理和性能
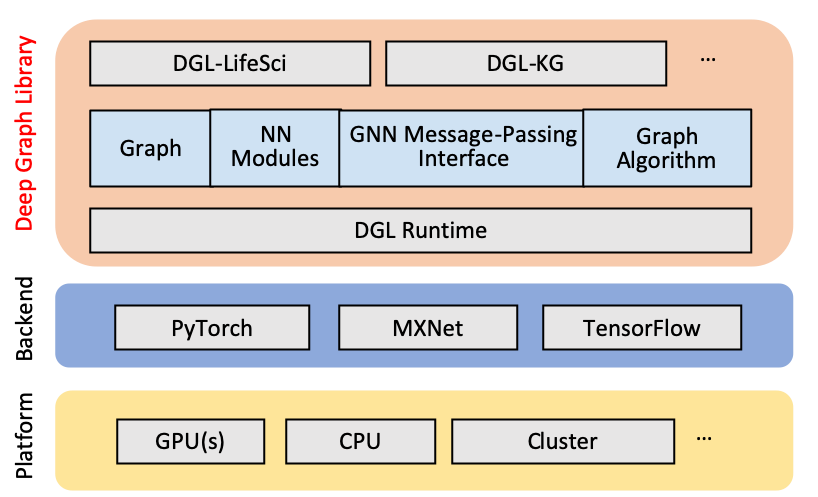
dgl是由纽约大学和亚马逊人工智能研究院共同推出的一款图神经网络python包。
具有高效、易用、可扩展的特点，兼容Pytorch、MxNet和Tensorflow三种底层框架。现在已迭代到0.5版本。
dgl框架以消息传递为核心，把图神经网络的计算过程抽象到消息传递机制中来，避免了传统的张量计算，在图神经网络实现方面达到了非常好的性能。
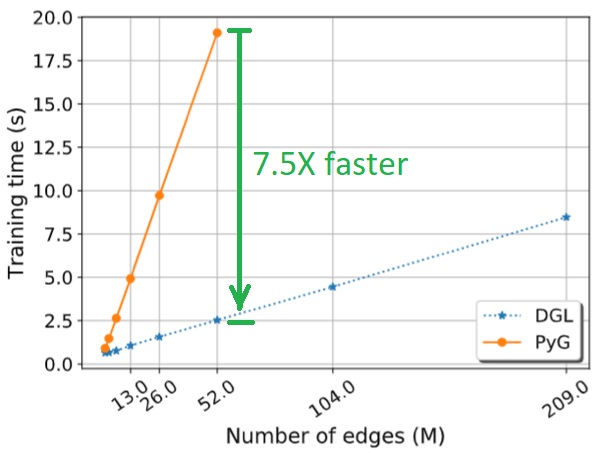
dgl高效的底层核心机制有：
- kernel fusion
- multi-thread and multi-process acceleration
- automatic sparse format tuning
- 消息传递机制上的优化
- 支持一机多卡、多机多卡GPU加速
1.3 DGL的消息传递机制
假设是点
v的特征，是边
(u,v)的特征，以下公式代表了DGL中的消息传递范式，
%7D%20%3D%20%5Cphi%20%5Cleft(%20xv%5E%7B(t)%7D%2C%20x_u%5E%7B(t)%7D%2C%20w%7Be%7D%5E%7B(t)%7D%20%5Cright)%20%2C%20(%7Bu%7D%2C%20%7Bv%7D%2C%7Be%7D)%20%5Cin%20%5Cmathcal%7BE%7D.%0A#card=math&code=%5Ctext%7BEdge-wise%3A%20%7D%20m%7Be%7D%5E%7B%28t%2B1%29%7D%20%3D%20%5Cphi%20%5Cleft%28%20x_v%5E%7B%28t%29%7D%2C%20x_u%5E%7B%28t%29%7D%2C%20w%7Be%7D%5E%7B%28t%29%7D%20%5Cright%29%20%2C%20%28%7Bu%7D%2C%20%7Bv%7D%2C%7Be%7D%29%20%5Cin%20%5Cmathcal%7BE%7D.%0A)
%7D%20%3D%20%5Cpsi%20%5Cleft(xv%5E%7B(t)%7D%2C%20%5Crho%5Cleft(%5Cleft%5Clbrace%20m%7Be%7D%5E%7B(t%2B1)%7D%20%3A%20(%7Bu%7D%2C%20%7Bv%7D%2C%7Be%7D)%20%5Cin%20%5Cmathcal%7BE%7D%20%5Cright%5Crbrace%20%5Cright)%20%5Cright).%0A#card=math&code=%5Ctext%7BNode-wise%3A%20%7D%20xv%5E%7B%28t%2B1%29%7D%20%3D%20%5Cpsi%20%5Cleft%28x_v%5E%7B%28t%29%7D%2C%20%5Crho%5Cleft%28%5Cleft%5Clbrace%20m%7Be%7D%5E%7B%28t%2B1%29%7D%20%3A%20%28%7Bu%7D%2C%20%7Bv%7D%2C%7Be%7D%29%20%5Cin%20%5Cmathcal%7BE%7D%20%5Cright%5Crbrace%20%5Cright%29%20%5Cright%29.%0A)
代表消息函数，作用在边上，它可以结合边特征和两端点的特征，在边上生成消息
代表汇聚函数，作用在点上，汇聚这个点收到的所有消息
代表更新函数，作用在点上，执行更新点属性的具体逻辑
三个函数组成了消息传递机制的主体，其中比较重要的是消息函数和汇聚函数，更新函数可有可无。
消息传递的核心逻辑是：
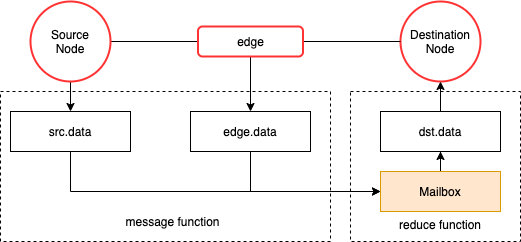
根据以上抽象，利用DGL的编程接口实现一个自定义图模型只需要提供这两个函数(更新函数可以不提供)，即message_function和reduce_function，前者用来指导如何对源节点的数据和边数据进行选择与加工然后传递到目的节点的邮箱；后者用来指导目的节点如何利用邮箱中它的邻居传递过来的消息和自身Embedding进行融合以更新自身Embedding。
接口层面，逐边计算函数是apply_edges(message_function), 该函数将逐边执行message_function并更新边属性。
逐点计算函数是update_all(message_function, reduce_function,update_function),该函数是一个高阶函数，会依次执行消息传递、汇聚和更新操作。DGL底层对这个高阶函数做了可观的优化。
最后可以总结出来，dgl中图神经网络计算的一般框架：在forward函数中调用message_function，reduce_function)和update_function，整合到apply_edges和update_all接口中去。
总结一下，消息传递机制的引入，给DGL带来的一个明显优势是，整个编程的抽象中不需要传递任何关于图结构的信息，即不需要边的邻接矩阵或者邻接表，边结构相关的信息在数据载入的过程中被底层的框架捕获并对上提供所需要的信息(主要是邻居的查询)，不需要用户在编程中进行干预。
1.4 消息传递的性能考量
dgl中对消息传递机制进行了优化，可减少内存耗用并提升计算速度。主要包括：
- 封装高端接口，如update_all, 合并多个内核操作在一个内核中
- 点和边上的并行：
- apply_edges -> generalized sampled dense-dense matrix multiplication (gSDDMM) operation
- update_all -> generalized sparse-dense matrix multiplication (gSPMM) operation
- 数据拷入边时的优化->
- 常规方法是将起点和终点属性拷贝到边上，在图中边很大的情况下，内存占用很大。
- dgl 中的built-in方法，使用entry index从点采样feature并拷贝，而不是完全拷贝
- 避免边上的特征序列化，
- 如果message和reduce函数都是built-in的，那么update_all操作都是在一个kernel中完成的
- 这样可以避免边上的特征序列化
给编写图神经网络代码带来的启示
- 使用
update_all调用时，尽量使用built-in的方法 - 使用
apply_edges方法操作边上的特征，可以尽量降低边上特征的纬度- 例如，可以将一些边上的复杂计算，部分地转移到点上
2 GCN
2.1 GCN概述
GCN(图卷积神经网络)的核心思想是利用『边的信息』对『节点信息』进行『聚合』从而生成新的『节点表示』。其理论基础是图信号处理延伸而来的图上卷积(类比于CNN中的卷积，只不过这是在非欧结构数据中)。
对GCN原理的理解，分为两种，频域和空域
- 频域：GCN的理论基础，涉及图信号处理领域理论和公式推荐，严谨而繁杂。参见
- 空域: 从消息传递的角度理解GCN的卷积操作，更好理解。
从以上两个角度出发，也可以得到GCN聚合的两种实现方式：
- 矩阵式聚合：在早期的研究中，由于没有什么并行库支持聚合节点信息，而图的规模往往很大。学术大佬们主要利用邻接矩阵的变换来完成这种聚合，然后使用 Pytorch 和 Tensorflow 这类库为矩阵运算加速。为了证明变换的有效性和合理性，很多工作借鉴了信号处理的思路，进行图上的傅里叶变换。
- 消息式聚合：随着图卷积越来越火，工业界逐渐加入了基础设施建设的队伍。借鉴 GraphX 等思路，出现一些不依赖邻接矩阵（或是屏蔽了邻接矩阵细节的）的消息聚合库，比较有名的有 PyG（比较早，实现多）和 DGL（比较新，易上手）。在这些库中，节点可以发出信息，并接受周围节点的信息，显式地完成消息聚合。在这种情况下，越来越多复杂的聚合方法出现了。
2.2 GCN理解
2.2.1 GCN公式
GCN的核心公式是：
%7D%20%3D%20%5Csigma(%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%5Ctilde%7BA%7D%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7DH%5E%7B(l)%7DW%5E%7B(l)%7D)%0A#card=math&code=H%5E%7B%28l%2B1%29%7D%20%3D%20%5Csigma%28%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%5Ctilde%7BA%7D%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7DH%5E%7B%28l%29%7DW%5E%7B%28l%29%7D%29%0A)
该公式代表了GCN网络中，节点特征是如何向下一层转移的。
其中,%7D#card=math&code=H%5E%7B%28l%29%7D)代表网络中的
层特征，
是非线性激活函数，
%7D#card=math&code=W%5E%7B%28l%29%7D)是这一层的权重矩阵，
和
分别是度矩阵和邻接矩阵(注意是所有节点自连后的计算出来的度矩阵和邻接矩阵)。
2.2.2 公式理解
上述公式是原论文中基于信号处理理论推导和正则近似得到的数学公式，较为繁琐，这里不做介绍。
仅从较为直观的角度，尝试去理解该公式的正确性。
- 从邻居出发
从一个点的所有邻居出发，可以推测出这个点的feature, 其消息聚合公式是
%20%3D%20%5Csum%7Bj%5Cin%20neighbor(i)%7DA%7Bij%7DXj%0A#card=math&code=aggregate%28X_i%29%20%3D%20%5Csum%7Bj%5Cin%20neighbor%28i%29%7DA%7Bij%7DX_j%0A)
其中是连边的权重，
是
在
。既然不相邻节点的系数
总为
，加上他们也不会对结果产生任何影响，所以上式可以写成：
%20%3D%20AX%0A#card=math&code=aggregate%28X%29%20%3D%20AX%0A)
这也就是当前的矩阵聚合公式。其中A是该图的邻接矩阵，X是图中所有点的特征矩阵。
添加自环
上述公式，仅考虑了邻居，聚合邻居特征来获取节点特征，缺失了节点自身的特性。
这里考虑加上自环。即自己和自己产生一条边，这样就可以把自身的特征加入进来。
那么矩阵聚合公式是：%20%3D%20(A%20%2B%20I)X%0A%20%3D%20AX%20%2B%20I%0A#card=math&code=aggregate%28X%29%20%3D%20%28A%20%2B%20I%29X%0A%20%3D%20AX%20%2B%20I%0A)
这里是只有对角线为1的单位矩阵，
代表添加了自环的邻接矩阵。
消息聚合公式是：归一化
上一步公式中的邻接矩阵，是没有归一化的，与特征
运算后，可能会导致特征的原有分布，带来不可预知的问题。
换到空域聚合的角度理解，即上述公式中，邻居个数越多的点，汇聚的特征越多，点的特征值就越大；而边缘的节点，汇聚的邻居特征少，点的特征值就会小。
这种不合理的情况，需要归一化操作来改善。
容易得到，归一化的消息聚合公式是：
这里是点
i的总度数。
矩阵聚合公式是：代表对这个图的度矩阵里面的每个值，求导数组成的矩阵。
注意，这里公式中之所以添加顶标~，是为了表示，这个是添加自环后的邻接矩阵和度矩阵。- 对称归一化
上一步的公式，仅考虑了采用点自身的度进行归一化，如果把这个点和邻居点的度同时纳入进入进来，归一化效果可能更好。
这里考虑采用几何平方数，那么消息聚合公式是：
这里i的度数，是点
j的度数。通过上式，可以剔除被聚合点j的度数对点i特征表达的影响。
矩阵聚合公式是：
至此，我们已经得到一个非常接近GCN公式%7D%20%3D%20%5Csigma(%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%5Ctilde%7BA%7D%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7DH%5E%7B(l)%7DW%5E%7B(l)%7D)#card=math&code=H%5E%7B%28l%2B1%29%7D%20%3D%20%5Csigma%28%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%5Ctilde%7BA%7D%5Ctilde%7BD%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7DH%5E%7B%28l%29%7DW%5E%7B%28l%29%7D%29)的形式
只不过GCN公式中加入了权重矩阵和激活函数。
公式中的重要一项，其实就是频域GCN理论中的对称正则化拉普拉斯矩阵(Symmetric normalized Laplacian)。
只不过频域理论中的GCN，涉及艰深的数学推导，我们这里从另一个角度对频域GCN公式进行解释和理解，也算是殊途同归。
2.3 DGL中的GCN实现
DGL中实现的神经网络基本都是按照消息传递机制编写的，GCN所依赖的空域聚合消息函数如下：
%7D%20%3D%20%5Csigma(b%5E%7B(l)%7D%20%2B%20%5Csum%7Bj%5Cin%5Cmathcal%7BN%7D(i)%7D%5Cfrac%7B1%7D%7Bc%7Bij%7D%7Dhj%5E%7B(l)%7DW%5E%7B(l)%7D)%0A#card=math&code=h_i%5E%7B%28l%2B1%29%7D%20%3D%20%5Csigma%28b%5E%7B%28l%29%7D%20%2B%20%5Csum%7Bj%5Cin%5Cmathcal%7BN%7D%28i%29%7D%5Cfrac%7B1%7D%7Bc_%7Bij%7D%7Dh_j%5E%7B%28l%29%7DW%5E%7B%28l%29%7D%29%0A)
其中，#card=math&code=%5Cmathcal%7BN%7D%28i%29)是节点
i的邻居集合，
是节点度的平方根，即
%7C%7D%5Csqrt%7B%7C%5Cmathcal%7BN%7D(j)%7C%7D#card=math&code=c_%7Bij%7D%20%3D%20%5Csqrt%7B%7C%5Cmathcal%7BN%7D%28i%29%7C%7D%5Csqrt%7B%7C%5Cmathcal%7BN%7D%28j%29%7C%7D)，
是激活函数。
可见该公式基本与2.2中最后的消息聚合公式一致，除了将边上权重全部置为1以外。
若有收获，就点个赞吧
0 人点赞
