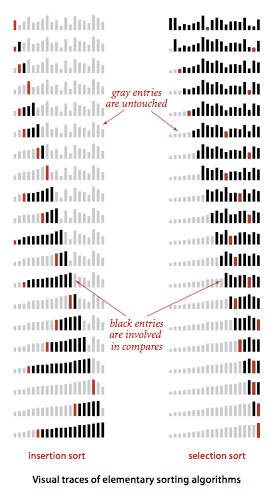
2.1 基本排序方法
- 冒泡排序:两两比较相邻记录,让较小的值不断向前走,就像是冒泡一样。第i次循环 ,就将第i+1小的值冒泡至a[i]
(通过不断比较并实时交换)
- 选择排序:不断选择剩余元素中的最小值,第i次,就找到第1+1小的值
(通过不断比较并记录最小值的index,最后才交换)
- 插入排序:保证i左侧的数据有序,然后下一次循环i++,考虑一条新数据,同样保证光标左侧的数据有序

less() 比较
exch() 交换
排序成本模型:考虑比较和交换的数量,访问数组的次数
可比较、可排序:需要实现Comparable接口—>有CompareTo()方法
CompareTo()方法必须实现一个全序关系:1 2 3
2.1.2选择排序
不断选择剩余元素中的最小值
需要N^2 比较和N次交换
- 运行时间和输入无关(一个有序数组或随机数组,所需时间是一样的),该算法不善于利用输入的初始状态。
- 数据移动是最小的,才交换N次。交换次数和数组大小是线性关系。
2.1.3插入排序
类似整理桥牌
插入排序(Insertsort)之Java实现
特点:当前索引左边的所有元素都是有序的,但是其最终位置还不确定。有可能发现下一个索引元素更小,则之前索引左边的某些元素将要右移,将这个最小的索引元素放到靠前的位置。
- 插入排序时间:取决于输入中元素的初始顺序。
- 对部分有序、小规模的数组十分有效
- 据说最好情况下(一个数组完全有序,那么只需要N-1次比较和0次交换)
- 当倒置(inversion)的数量很少时,插入排序可能比本章中任何其他算法都快
- 如果是一个已经排好序的数组,那么很快就可以结束循环
2.1.6 希尔排序
基于插入排序的一种算法,可以用于大型数组
第一批突破O(n2)复杂度的排序算法
- 更高效的原因是,权衡了子数组的规模和有序性
- (划分的子数组规模小,且部分有序,这两个特性都是插入排序的优势点)
- 将插入排序的每次的增量从1,变成了k
关键是如何选择增量序列?仍是数学难题,现在还没有找到最好的
不稳定的排序算法,平均复杂度,O(nlogn)~O(n2)
2.2归并排序
是一种稳定的排序方式
性质:数组长度N,排序时间复杂度O(NlogN),额外空间O(N)
归并排序:将数组分成两半分别排序,然后将结果归并起来。是分治思想的典型体现
- 原地归并
将两个排序的子数组,归并成一个大的已排序数组
- 自顶向下的归并排序
从大分到小,使用递归,但实际上最终还是从两个元素开始归并。需要0.5NlgN至NlgN次比较,最多需要访问数组6NlgN次。
三个建议:
1、对小规模子数组使用插入排序
2、测试数组是否已经有序
3、不将元素复制到辅助数组
- 自底向上的归并排序
从两个到多,使用迭代。需要0.5NlgN至NlgN次比较,最多需要访问数组6NlgN次。
比较适合于用链表组织的数据
归并排序告诉我们,当能够用其中一种方法解决一个问题时,你都应该试试另一种。(分治方法:自顶向下或者自底向上)
归并排序是一种渐进最优的基于比较排序的算法
归并排序的主要缺点: 辅助数组所使用的额外空间与N的大小成正比
排序算法的复杂度
没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。(借用二叉比较树可以证明)
2.3快速排序
20世纪十大算法之一
冒泡排序的升级,属于交换排序类
可能是应用最广泛的排序算法了,原因是实现简单,适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多,而且是原地排序,时间复杂度是O(nlgn)
优点:原地排序,只需要一个很小的辅助栈(递归操作的栈,所以空间复杂度(logn))
缺点:很脆弱,容易发挥不佳
潜在缺点:切分不平衡时,性能很低效
快速排序平均需要~2NlnN次比较(以及1/6的交换),最多需要约N2/2次比较,但随机打乱数组能够预防这种情况。
最好的情况是,每次都将数组对半切分
快速排序的改进: 1、小数组插入排序更快,所以小数组用插入排序 2、三取样切分,取三个元素比较用中间大小的元素作为切分元素。 3、熵最优排序,重复值较多时用三向切分,即分为大于、等于、小于。
对于只有若干不同主键的随机数组,三向切分快速排序是线性的。对于大小为N的数组,三向切分快速排序需要~(2ln2)NH次比较,其中H为由主键值出现频率定义的香农信息量。
三向切分的快速排序:适用于对有大量重复元素的数组排序;对于含有大量重复元素的数组,其排序时间从线性对数级别降低到了线性级别
- 元素的概率分布决定了信息量的大小,没有任何基于比较的排序算法,能够用少于信息量决定的比较次数完成排序。
难道还有完全不需要比较的排序算法?
归并排序和快排的比较 归并排序:先递归(sort),再处理数组(merge) 比较次数少 快速排序:先处理数组(partition),再递归(sort) 移动次数少
- merge()
- 将两个有序数组合并为一个新的有序数组
- 指针i访问左边,指针j访问右边
- 两者比较值,取小值放到新数组,不断循环,完成归并
- partition()
- 将数组切分为两块,前一部分都小于a[lo],后一部分都大于a[lo]
- 指针i访问左边,向右扫描,直到在左边找到第一个比v大的元素
- 指针j访问右边,向左扫描,直到在右边找到第一个比v小的元素
- 交换,不断循环,v成为左右两个子数组的分界值
merge 和partition中都有两个指针,来分别对分治的左右两个数组进行访问 908
快速排序 partition函数的所有版本比较
http://www.tuicool.com/articles/Mz6Jvy3
2.4 优先队列
- 优先队列:删除最大元素delMax、插入元素insert
- 队列:删除最老元素、插入元素
- 栈:删除最新元素、插入元素
优先队列的应用场景:系统优先级、任务调度
优先队列的实现:无序数组实现,有序数组实现,链表表示,堆实现
时间复杂度:
| 数据结构 | insert() | delMax() |
|---|---|---|
| 有序数组 | N 类似于插入排序 |
1 |
| 无序数组 | 1 | N 类似于选择排序 |
| 堆 | logN | logN |
2.4.3堆的定义
堆有序:一个二叉树的每个结点都大于等于他的两个子节点
根节点是堆有序的二叉树中的最大节点
二叉堆:
- 一种优秀的实现优先队列的数据结构
- 定义:二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级储存(不使用数组的第一个位置)。
基于数组的堆实现:在数组中无需指针,即可保证沿树上下移动的便利,算法保证了对数级复杂度的性能。数组实现完全
二叉树—>二叉堆
k -> (2k,2k+1)
由下至上的堆有序化、上浮swim
- —用于插入,跟上面比,跟更靠近根节点的点比较
由上至下的堆有序化,下沉sink
- —用于删除最大元素,跟下面比,跟自己的子节点比
索引优先队列:可以在任意位置插入(insert)和删除(delete)节点
或者理解为可以快速访问其中最小元素的数组
2.4.5 堆排序
对于无序数组实现的优先队列,反复找出(删除)最小元素,相当于插入排序
对于堆实现的优先队列,反复找出(删除)最小元素,也就是一种全新的排序方法 -> 堆排序
堆排序步骤:
- 堆的构造:将无序序列构造为堆
- 下沉排序(销毁堆):输出堆顶元素,调整剩余元素为一个新的堆(使用sink方法)->
- 其实是一个堆的销毁过程,之前用来存储堆的数组,变成了存储最后排序结果的数组。
- 大顶堆-> 删除最大值-> 最大值最先出来,放在最后->最小值最晚出来 ,放在最前面 -> 有小到大排序
- 小顶堆-> 删除最小值-> 最小值最先出来,放在最后->最大值最晚出来 ,放在最前面 -> 有大到小排序
堆提供了一种,从未排序的部分,找到最大元素的有效方法
改进:先下沉,再上浮;需要额外空间
- 堆排序:唯一的能同时最优利用时间和空间的方法。辅助空间O(1)
- 嵌入式设备中使用较多,但是现代系统中较少使用,因为无法利用缓存(数组元素基本不与相邻元素进行比较)。
- 堆排序也属于选择排序的一种
大顶堆 => 小到大的堆排序
小顶堆 => 大到小的堆排序
海量数据TopK问题,如果是最大的TopK,用小顶堆
比如海量数据求前n大,利用小顶堆,我们比较当前元素与最小堆里的最小元素(即堆顶元素),如果它大于最小元素,则应该替换那个最小元素,并调整堆的结构,持续这一过程,最后得到的n个元素就是最大的n个。
海量数据TopK问题,如果是最小的TopK,用大顶堆
比如海量数据求前n小,利用大顶堆,我们比较当前元素与最大堆里的最大元素(即堆顶元素),如果它小于最大元素,则应该替换那个最大元素,并调整堆的结构,持续这一过程,最后得到的n个元素就是最小的n个,这样可以扫描一遍即可得到所有的前n小元素,效率很高
2.5 应用
- java待排序序列中元素,使用的都是引用,因此排序中的交换成本是廉价的,甚至低于比较的成本
- java中Arrays.sort()主要使用三向切分的快速排序(对于原始数据类型)和归并排序(对于引用数据类型)
中位数选择算法(即数组中第k小的数问题,剑指offer30题)