后缀表达式:不需要括号区分运算符的优先级,可以直接求值。例如:ABCD-*+EF/-
中缀表达式:需要括号来区分优先级,如:A+B*(C-D)-E/F
表达式树: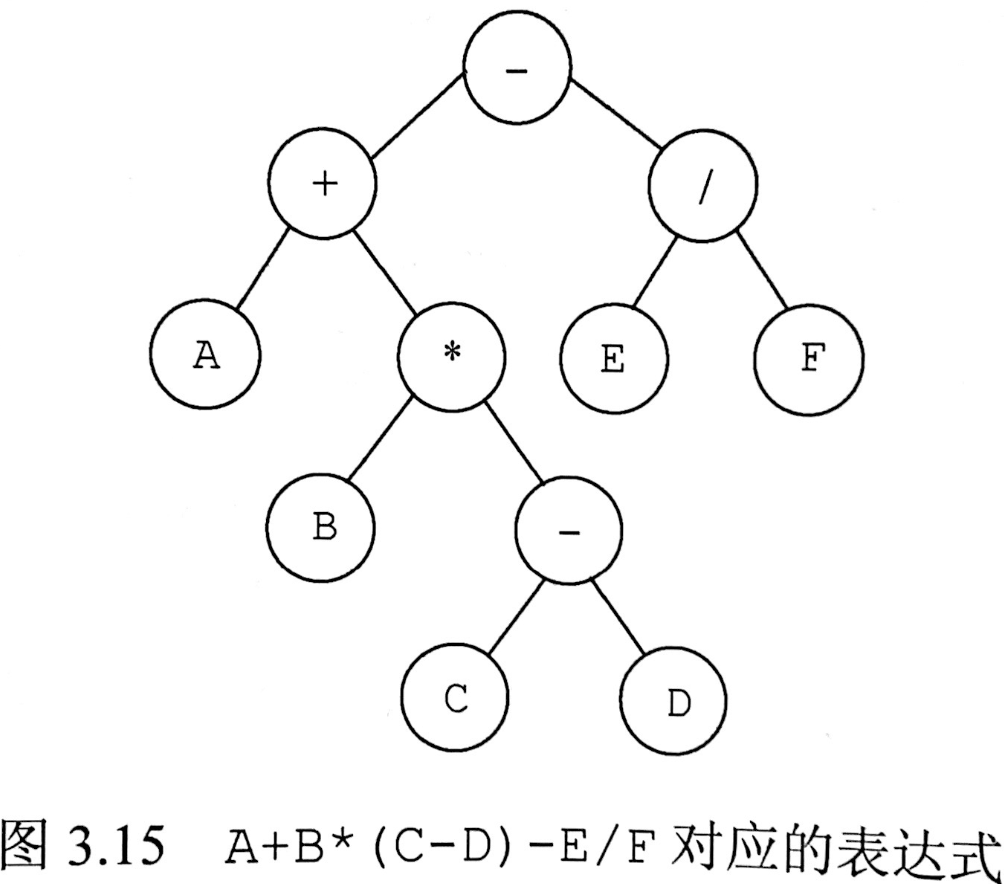
表达式相互转换
1. 前/后缀表达式 -> 中缀表达式
可以轻松的利用栈来实现,栈的元素是操作数的字符串,如:["a", "b+c", "d"]
2. 中缀表达式 -> 后缀表达式
转换的算法:按顺序读入表达式
- 如果遇到操作数,直接输出
- 如果遇到
(,放入栈中;如果遇到),则输出栈中的操作符,直到遇到(符号 - 如果遇到
+-,则让栈中的所有+-和*/都出栈 - 如果遇到
*/,则让栈中的*/出栈
上述规则是如何得出的?
以如下的情况为例:
- 如果栈中是
*,当前读到的表达式为+,那么意味着当前层级的表达式是这种情形:A * B +,操作数A和B已经输出了,那么这个时候只需要将*出栈,再将+入栈即可。
注:
- 为了简化操作,可以在中缀表达式的前后都加上
#符号 - 中序表达式转化为后续表达式时,数字的顺序是不变的
几个练习:
- 中序表达式:
a+b-a*((c+d)/e-f)+g,后续表达式:ab+acd+e/f-*-g+ - 中序表达式:
a/b+(c*d-e*f)/g,后续表达式:ad/cd*ef*-g/+
表达式求值
1. 前缀/后缀表达式求值
前缀表达式和后缀表达式可以非常轻松地利用栈来求值
2. 中缀表达式的求值
需要借助中序表达式转化为后续表达式的算法。
首先需要非常熟悉「中序表达式 -> 后续表达式」的算法
需要用到两个栈:
- 一个栈存放操作数
- 个栈存放操作符号,就像在「中序表达式 -> 后续表达式」那个算法的一样
计算过程:
- 按顺序读入表达式
- 每当 1 个操作符出栈时,就用这个操作符去计算「操作数栈」的栈顶两个元素,再将结果入栈
表达式树 -> 表达式
只需要按照不同的遍历方式进行即可
前缀表达式和后缀表达式不需要加括号
中缀表达式需要加括号,加括号的时机:子节点是 + -,父节点是 * / 时,需要对子树加括号
表达式 -> 表达式树
1. 前/后缀表达式 -> 表达式树
可以利用栈来轻松实现
栈中的元素是树的节点
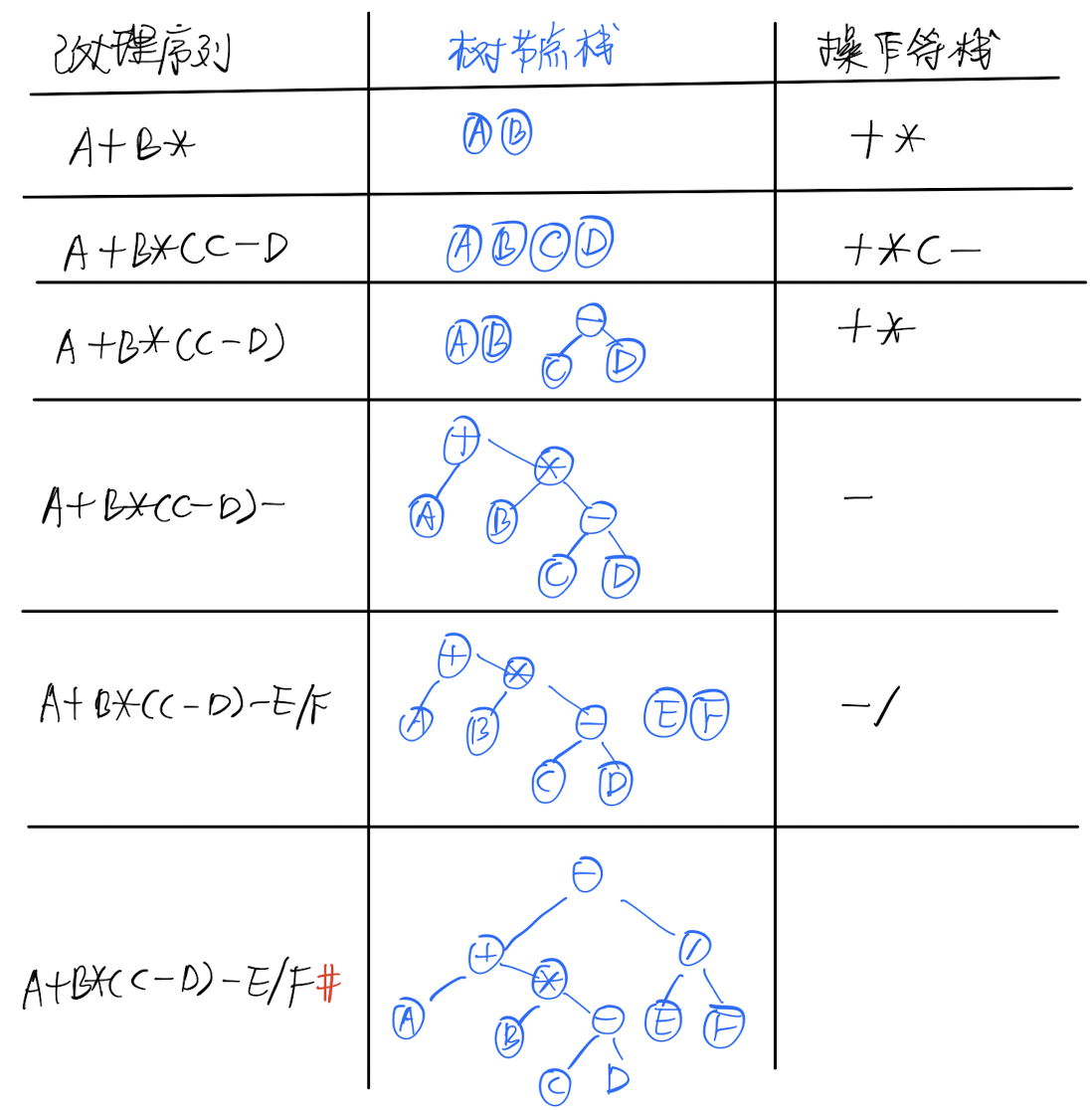
2. 中缀表达式 -> 表达式树
首先需要非常熟悉「中序表达式 -> 后续表达式」的算法
需要用到两个栈:
- 第一个栈用于存放树的节点
- 第二个栈用于存放操作符,就像在「中序表达式 -> 后续表达式」那个算法的一样
计算过程:
- 按照顺序读入表达式
- 「操作符栈」有操作符出栈时,用这个操作符来组合「节点栈」栈顶的两个节点,并将结果放回「树节点栈」中。
例子:中序表达式 A+B*(C-D)-E/F