图的基本概念

图

• 表示定点的集合，顶点的表示方法：
• 表示边的集合，边的表示方法：
  • 无向图：
  • 有向图：

完全图

任意两个顶点之间都存在边

• 完全有向图中，边的数量为：
• 完全无向图中，边的数量为：

注：注意区别「完全图」和「连通图」的概念。

子图

从原有图中取出一部分可以得到子图。如果一个图 满足： 且 ，那么 即为 的子图。

连通

• 连通图：无向图中任意两个顶点之间都存在路径
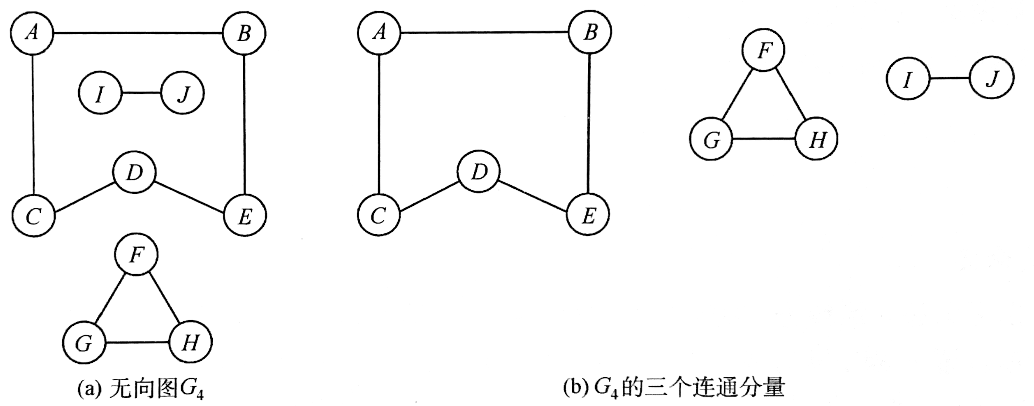
• 连通分量：无向图中极大的连通子图
• 强连通图：有向图中，任意两个顶点之间都存在两条互相的路径
• 强连通分量：有向图中，极大的强连通子图

连通图的数量关系：有 个顶点的无向图，最少有多少条边，可以确保得到的图一定是连通的： 。其中 个顶点构成完全图，最后再加一条边即可。

生成树

包含图的全部顶点的极小连通子图（极小，意味着边尽量少）

度的数量关系

• 无向图中，全部顶点的度之和等于边数的 2 倍，因为一个边带来 2 个度。即：。
• 有向图中，所有顶点的入度和出度之和相等，且等于边的数量。即：。

网

边具有权重的图叫做带权图，或者网。

稀疏图和稠密图

判断依据为：。

路径

• 简单路径：顶点不重复的路径序列。
• 简单回路：除了第一个和最后一个顶点，中间不出现重复顶点的回路。

判断图中是否存在回路：

• 利用 DFS：如果深度优先生成树中存在从子孙指向祖先的回边，则说明存在回路。
• 逐个删除顶点：
  • 无向图中：删除度 的顶点，最后剩余的就是回路
  • 有向图中：删除度 的顶点，最后剩余的就是回路