二叉树

特殊的二叉树

满二叉树
完全二叉树
平衡二叉树：任意节点的左右子树深度之差不超过 1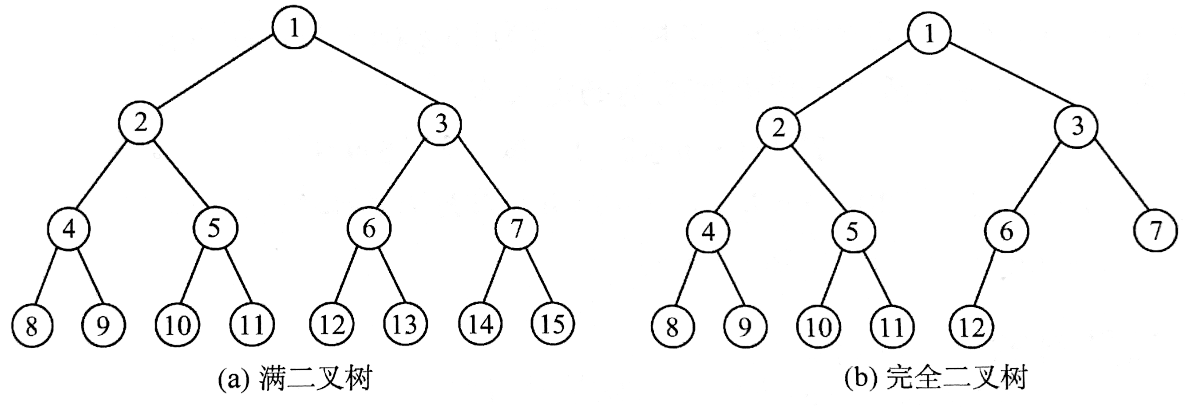

数的数量特征

完全二叉树的特征：
如果按照编号 1 开始编号：

• 编号 的节点的父节点为 ；左子为 ，右子为
• 若节点总数为 ，则叶子节点的个数为

节点的度与节点数量的关系：
设节点总数为 ，度为 的节点数量为 ，度为 的节点数量为 ，叶子节点数量为 ，则有：

• 节点总数：
  • 其中 表示所有度为 的节点的孩子数量， 类似， 表示根节点
• 叶子节点数：

二叉树的存储结构/实现

顺序实现

这种实现适合完全二叉树
注：在实现的时候，为了便于计算，应该将跟节点存放在数组下标 1 的位置

顺序实现	二叉树

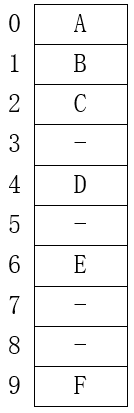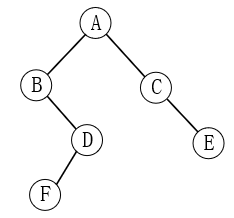链式实现

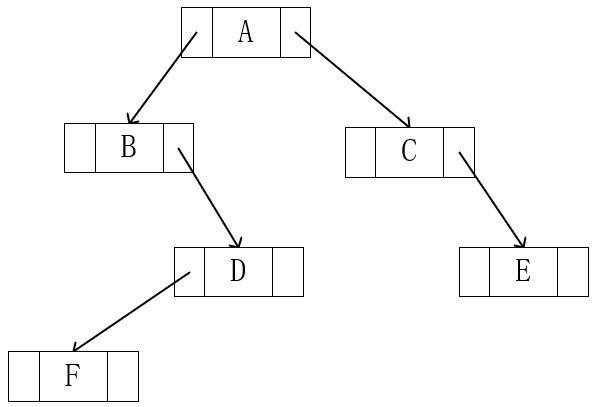
二叉链实现时，空链域的数量为：

二叉树的遍历

迭代算法中， 个节点的二叉树最多有 层，栈最多也 层，因此空间复杂度为：

二叉树遍历的规律：

• 中序遍历的最后一个节点：不一定是叶子节点，一直向右走（不能向左走）即可得到这个节点
• 前序遍历的最后一个节点：一定是叶子节点，而且是叶子中最右边的一个。（反证法可以证明）
• 后序遍历的第一个节点：一定是叶子，而且是叶子中最左边的一个。（反证法可以证明）
• 前序，中序，后序遍历时，所有叶子节点的顺序都是相同的。（可以通过找到最下面的一个公共祖先节点来证明）
• 已知前序遍历序列和后序遍历序列，可以知道两个节点是否有祖先关系。例如：如果前序有 ...A...B... 的顺序，后序有 ...B...A... 的顺序，则说明 A 是 B 的祖先。（可以用反证法证明）

中序遍历

迭代写法
「TODO」这个需要记住

前序遍历

迭代写法
「TODO」这个需要记住

后序遍历

迭代写法
「TODO」分析以下

可以得到祖先节点到子节点的路径，栈里面就是路径。

层序遍历

由遍历序列构造二叉树

已知以下组合时，可以还原出二叉树：

• 「先序序列」和「中序序列」
• 「后序序列」和「中序序列」
• 「层序序列」和「中序序列」

因为：

• 由先序/后序序列可以得到树的根节点
• 根节点可以将中序序列划分为两个子序列

例如：对于<前序遍历，中序遍历>的情形，使用前序遍历的递归来求解：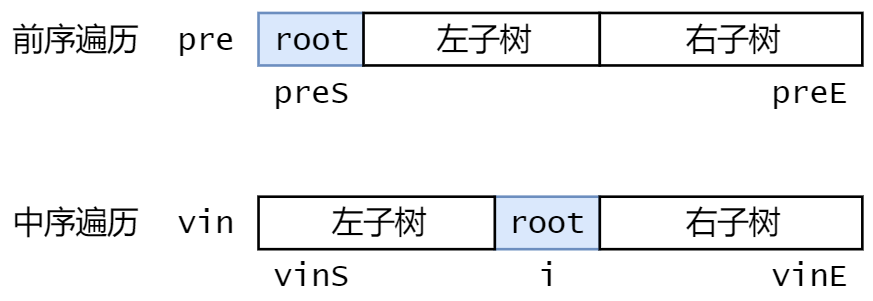

TreeNode* setNode(const vector<int>& pre, int preS, int preE,
                  const vector<int>& vin, int vinS, int vinE) {
    if (preS > preE)
        return NULL;
    TreeNode* node = new TreeNode(pre[preS]);
    for (int i = vinS; i <= vinE; ++i) {
        if (vin[i] == pre[preS]) {
            node->left = setNode(pre, preS + 1, preS + i - vinS, vin, vinS, i - 1);
            node->right = setNode(pre, preS + i - vinS + 1, preE, vin, i + 1, vinE);
            break;
        }
    }
    return node;
}

前序序列可以对应多少个二叉树：

• 由于一个前序序列和一个中序序列可以唯一确定一棵二叉树
• 考虑对一棵二叉树进行中序遍历，采用递归的算法，则：元素入栈的顺序符合前序序列，元素出栈的序列符合中序序列
• 因此，问题转化为给定入栈顺序，求合法的出栈顺序数量，即为卡特兰数
• 可以证明：合法的出入栈顺序，其对应的前序序列和中序序列，一定可以构造出一棵二叉树