B树和B 树

B树

B树的特征

B 树的示意图：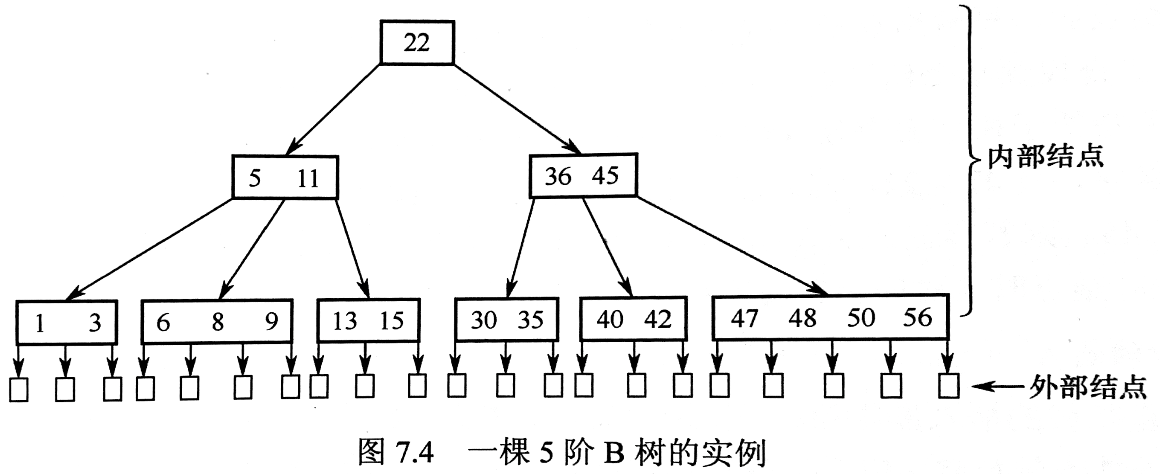

注：最后是「外部节点」，实际并不存在这些节点。叶子节点相应的指针为空。

B 树的定义：

• B 树是指「多路平衡查找树」。
• 阶B树：每个结点最多拥有 棵子树，最少拥有 棵子B树；根节点不是叶子的话最少拥有2棵子树
• 所有的叶子都在同一层，B 树的平衡因子为

B 树节点的例子：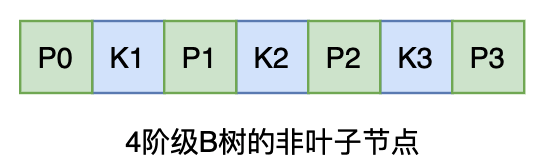

其中：

• K 表示关键字，P 表示指向子树的指针
• P 和 K 都是有序的

B 树的高度分析： 阶，高度为 （不包括最后一层的「外部节点」），共有 个关键字：

• 「外部节点」数量比关键字数量多

• 最多的情况：有 个节点，每个节点有 个关键字，最多有 个关键字。因此，高度

• 最少的情况：第 层有 个叶子节点，因此共有 个「外部节点」。通过「外部节点」和关键字数量的关系可知，最多有 个关键字。因此，高度

B树的操作

插入操作

基本原则：找到最底层的叶子节点，进行插入操作。如果插入后关键字数量大于 ，就进行「分裂操作」。

分裂：

• 找到第 的关键字（考虑 3 个关键字的情形即可），将关键字分为三部分。
• 左边部分留在原来的节点中；中间部分放入父节点的关键字中；右边部分放入新的节点中
• 如果父节点也溢出，则继续分裂父节点。最终可能导致 B 树增高

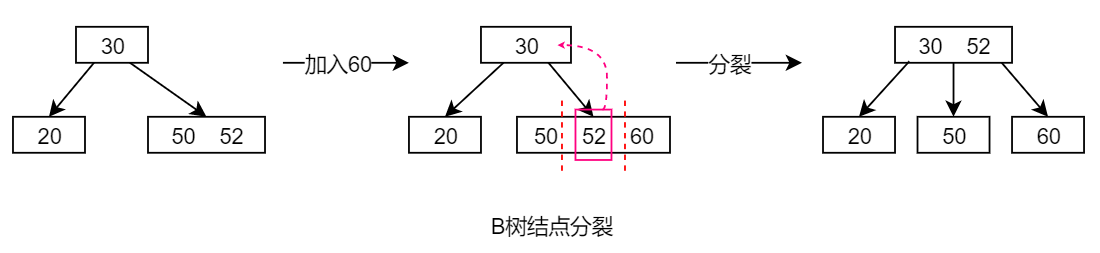
插入导致 B 树增高的情况（3 阶 B 树）：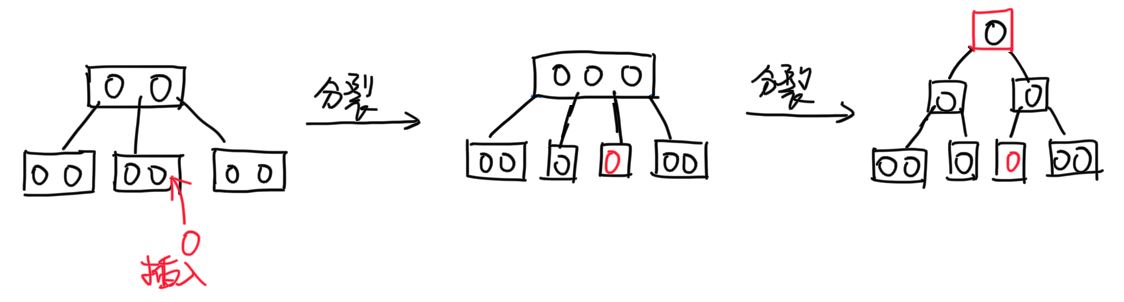

删除操作

如果删除操作发生在「非终端节点」，那么可以从子节点借一个关键字，替代被删除的位置。最终，问题转化为在最后一层删除节点。

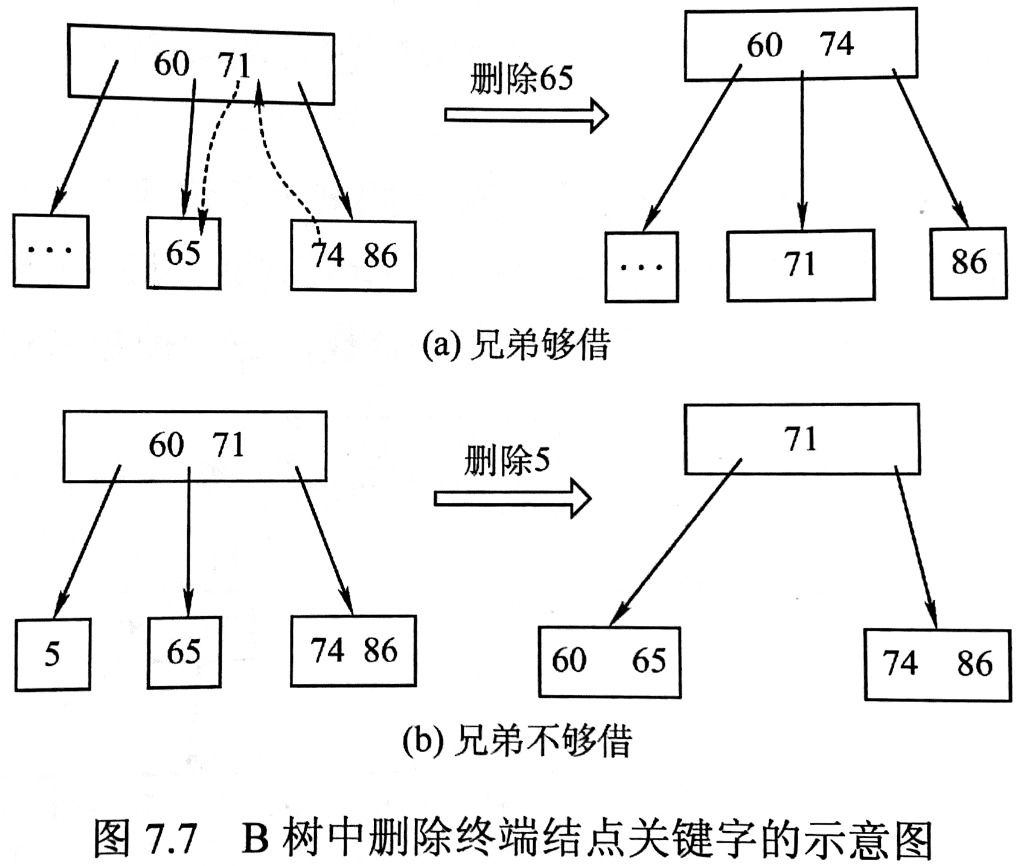
从终端节点删除关键字的情形：

• 情形1：直接删除。（即：当前节点关键字数量 ）
• 情形2：向兄弟节点借（即：当前节点关键字 ，兄弟节点 ）。借的时候要从父节点那里过一下
• 情形3：兄弟节点不够借（即：当前节点和兄弟节点都只有 个关键字），向父节点借一个，并且与删除后的部分一起合并到兄弟节点中。
  • 如果导致父节点关键字不足，则父节点可以向子节点借（转化为情形 1）；
  • 如果子节点没法借，那么继续向父节点借并进行合并操作。

删除操作导致 B 树高度降低（3 阶 B 树）：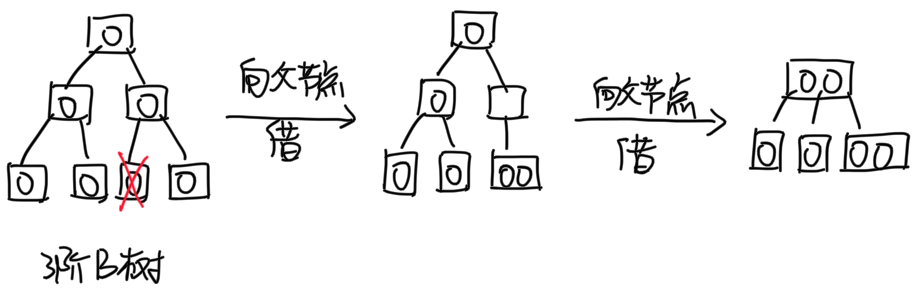

B+树

B+ 树的特征：

• 结点关键字个数和子树个数相同
• 叶结点包含整棵树的全部关键字，叶节点链接在一起
• 分支节点的关键字为子树关键字中的最大值
• 数量关系：非叶子的根节点至少有 2 棵子树；其余节点至少 棵子树，最多 棵子树

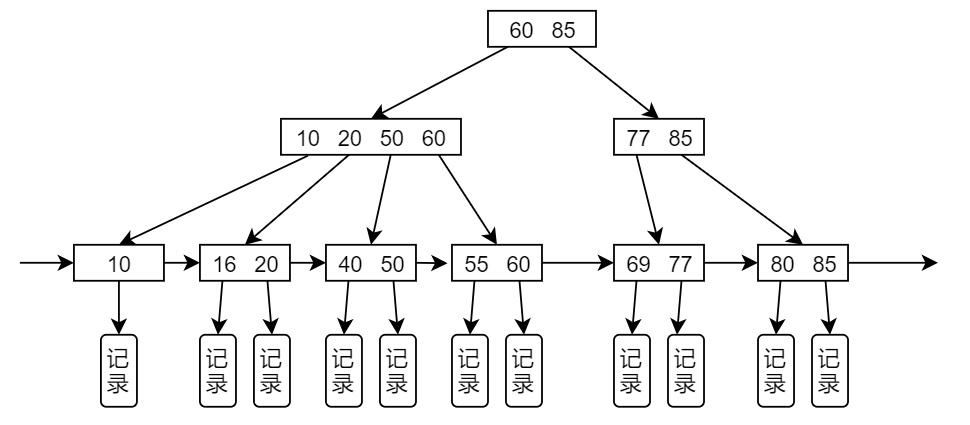
B+ 树的查找：

• 分支节点仅仅是子树中关键字的副本/索引
• 就算在中途找到了关键字，也必须到叶子节点才能停止

注：B+ 树非常适合数据库索引和文件系统索引。