串

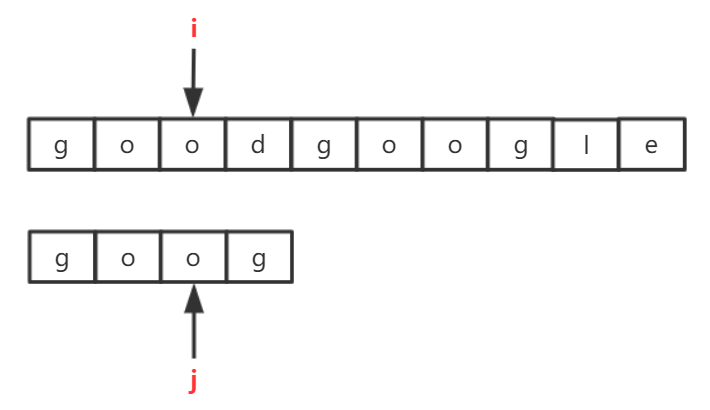
子串

子串的第一个字母在主串中的位置成为子串的位置，如：
acc 在 acc aoe 中的位置是 1

串的存储

1. 顺序存储

长度固定的顺序存储：
例如：char str[MAXLEN]

动态长度的顺序存储：
例如：malloc 申请内存

2. 串的块链实现

类似于顺序表的链式存储。
每个块里面可以只存储 1 个字符，也可以如下图存储 4 个字符。不足的部分用 # 补足。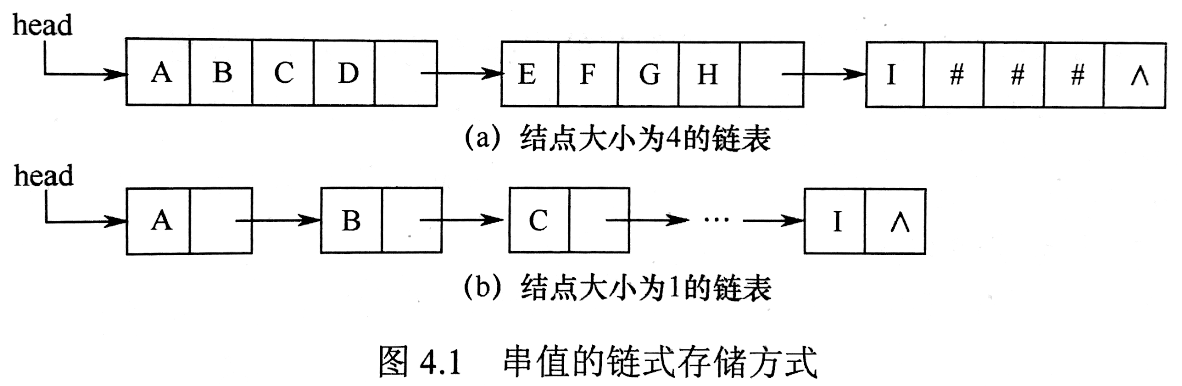

模式匹配：暴力方法

暴力方法（BF）：匹配失败时 i 指针和 j 指针都要回溯

模式匹配：KMP

1. 一个例子

有这样一个模式串： abc1234abc56，如果在和主串比较到 5 的时候失败，那么可以知道：

• 主串 i 指针之前的内容应该是：abc1234abc
• 由于模式串中 abc1234abc 的头三位和尾三位都是 abc，因此，只需要移动 j 指针指向模式串的字符 1 即可

2. KMP 的原理

根据上述的例子可以知道，由于模式串自身的规律，在匹配失败的时候，i 指针和 j 指针都没有必要完全回退。

这种规律就是部分匹配值，它是指：给定一个串，最长的前后缀相等的长度，例如：

• ab123ac 的部分匹配值为 0
• ab123ab 的部分匹配值为 2
• ab12ab1 的部分匹配值为 3

如果在模式匹配时失败了，就看失败位置前方的模式串，如果其部分匹配值是 k，就将 j 指针移动到模式串的第 p[k] 位置。

• 就上述例子，失败位置前方的模式字符串为 abc1234abc，部分匹配值为 3，因此将 j 指针移动到模式串的 [3] 位置，指向 1 这个字符

3. 算法实现

为了计算机查表方便，计算出模式串每一位的 next 值，该值的含义是：

• 如果 next 为 -1，需要将 i 指针移动到下一位。表示连第一位都匹配不成功
• 如果 next 为 k，那么 i 指针不动，j 指针指向模式串的 [k] 位置继续匹配

next 值等于模式串当前位之前的部分匹配值，第一位固定为 -1
例如：模式串 ababc 对应的 next 数组为：[-1 0 0 1 2]

如何计算 next 数组，也就是如何计算出部分匹配值：
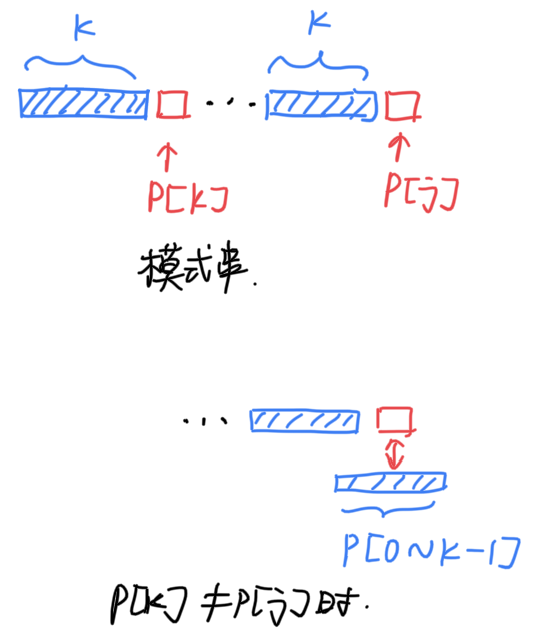
已经计算出了第 j 位之前的部分匹配值，设该值为 k。考察第 k 位与第 j 位：

• 如果这两个字符相等，那么说明第 j+1 位之前的部分匹配值为 k+1。（可以用反证法证明，无法找到更长的部分匹配值了）
• 如果这两个字符不相等，就又回到了字符串匹配问题：此时的模式串是 p[0 ~ k-1]，匹配到第 j 位的时候失败了，根据已经计算出的 next 表来回溯，继续匹配。

4. KMP 的优化

考虑下图的情况：
当前匹配失败，j 指针进行回溯；回溯之后仍然匹配失败，再回溯；
上述的有几次回溯过程是不必要的，因为 p[next[j]] == p[j]，当前这一位的 next 值应该是 -1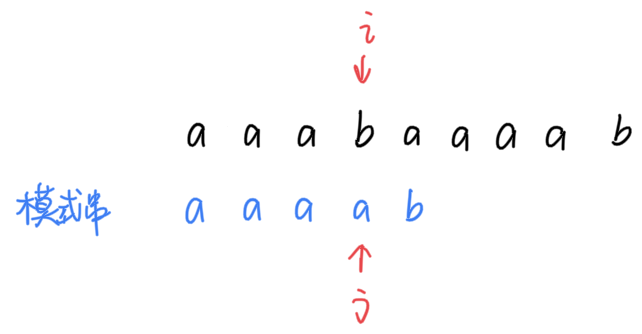

如何优化：

• 在计算出一个模式串某一位的 next 值时，如果有 p[j] == p[next[j]]，那么应该直接将这一位的 next 设为 next[next[j]]

上述情况下，未优化过的 next 数组为 [-1 0 1 2 3]
优化过后的 next 数组为 [-1 -1 -1 -1 3]

5. KMP 的有穷自动机理解

从有穷自动机的角度来理解 KMP
next[] 数组和 pat 合起来组成了一个有穷自动机，其中 next[] 表示状态的回溯
以模式串 "ababc" 为例，其状态机为：

实现代码：

/**
 * @brief 根据模式串 pat 生成 next 数组
 * @param len 模式串 pat 和 next 数组的长度
 */
void genNext(int len, char* pat, int* next)
{
    int j = 0;
    int k = -1;
    next[0] = -1;
    while (j < len - 1) {
        if (k == -1 || pat[j] == pat[k]) {
            next[++j] = ++k;
        }
        else {
            // 利用已经匹配的模式串的信息，来计算最大的回溯位置
            // 这个过程可能会重复几次
            k = next[k];
        }
    }
}
/**
 * @brief 进行 KMP 匹配
 * @return 成功，返回初次匹配的位置；失败，返回 -1
 * @param text_len 待匹配字符串的长度
 * @param pat_len 模式串的长度
 */
int KMP(char* text, int text_len, char* pat, int pat_len)
{
    int i = 0;
    int j = 0;
    int* next = NULL;
    next = malloc(pat_len * sizeof(int));
    genNext(pat_len, pat, next);
    while (i < text_len && j < pat_len) {
        if (j == -1 || text[i] == pat[j]) {
            // text[i] == pat[j] 表示当前字符匹配
            // j == -1 表示跳过当前的 text[i]
            i++;
            j++;
        }
        else {
            j = next[j];    // 回溯
        }
    }
    if (j == pat_len) {    // 成功，返回初次匹配的位置
        return i - j;
    }
    else {                 // 失败，返回 -1
        return -1;
    }
}