堆

堆的性质

大根堆的定义：父节点的值大于等于子节点的值。
小根堆的定义类似

大根堆的示意图：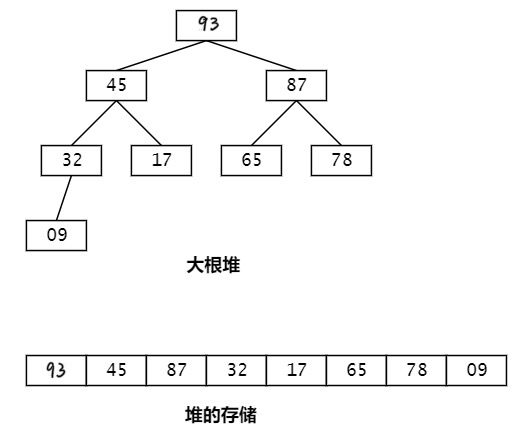

堆的存储：堆是「完全二叉树」，所以可以使用数组存储

堆的维护

删除堆顶元素

删除堆顶元素后，会将堆中最后一个元素填充到堆顶位置，然后通过「Adjust Down」的操作将这个元素调整到适合的位置。

Adjust Down：根节点的左右子树已经是堆了，只需要不断地让当前元素下降即可。

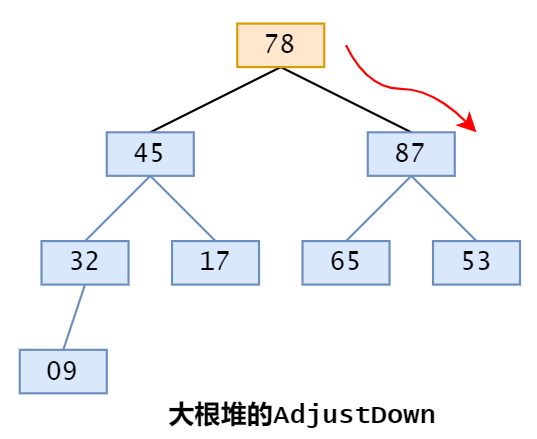
向堆中增加元素

将新元素放在堆的最后，然后通过「Adjust Up」操作将该元素调整到合适的位置

Adjust Down：前方的结点已经是堆，只需要让当前节点不断向上即可。

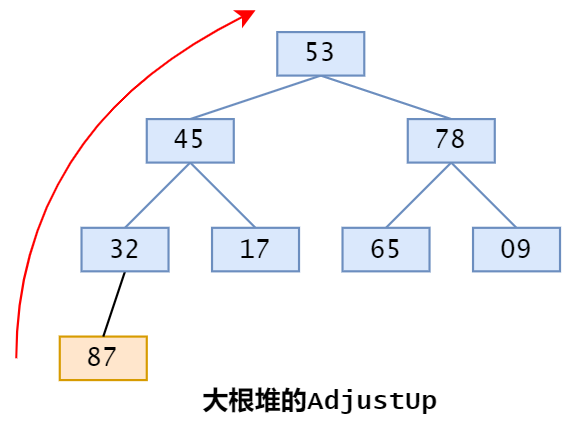
初始化堆

从下到上的建立方法：

• 初始序列可以构成「完全二叉树」，元素数量为
• 从第 个元素开始向前调整：当前节点的子树已经是堆了，将当前元素当作根节点，进行「Adjust Down」操作即可。

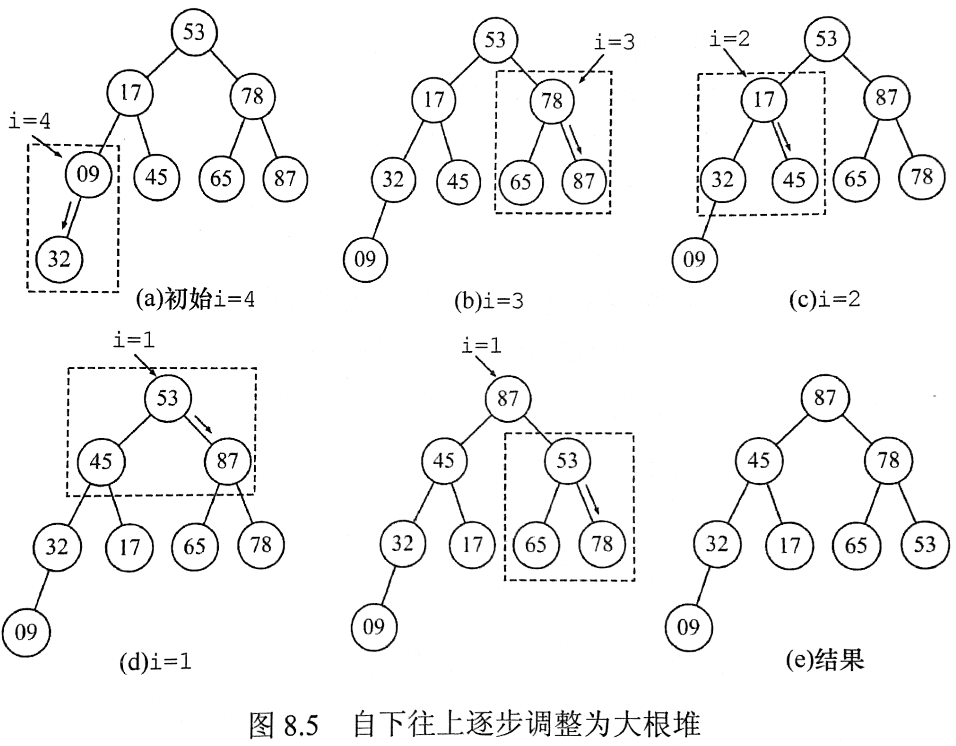
初始化的时间复杂度：

以满二叉树为例，共 层，节点数量 个。从第 层开始调整，调整到第 层，每层共 个节点，每个节点最多需要 次调整，共需要调整次数为： 令 ，则有： 因此：，即 复杂度

从上到下的建立方法：从第 个元素开始向后调整：当前节点的前方已经是堆了，问题等价于不断地将第 个节点加入到前方的堆中。不断进行「Adjust Up」操作即可。

堆的应用

• 优先队列的实现：堆直接就是优先队列。
• 堆排序
• 大规模数据，求最大的前多少个数：使用大根堆实现。