外部排序的基本思路
- 对文件进行分块,分别对每一块文件进行「内部排序」
- 对于有序的文件块,进行「归并排序」
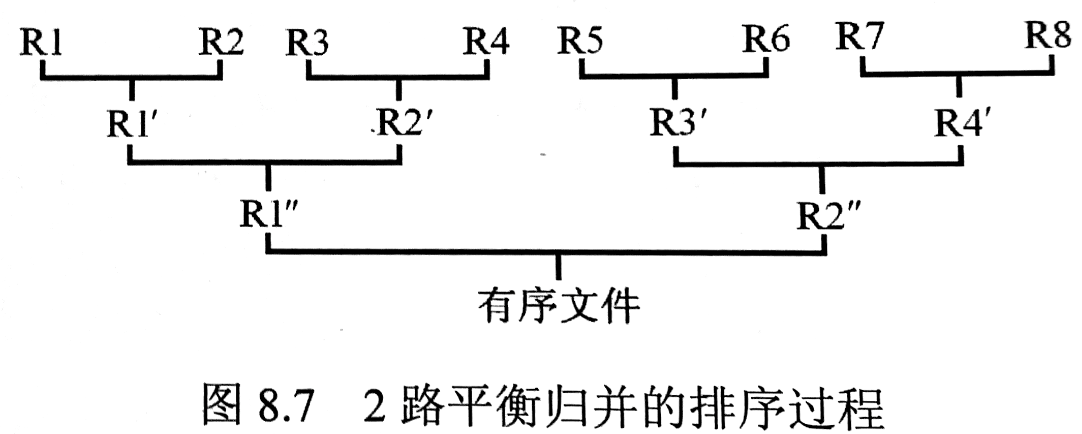
将两个有序子文件 归并为新的有序子文件
的过程为:
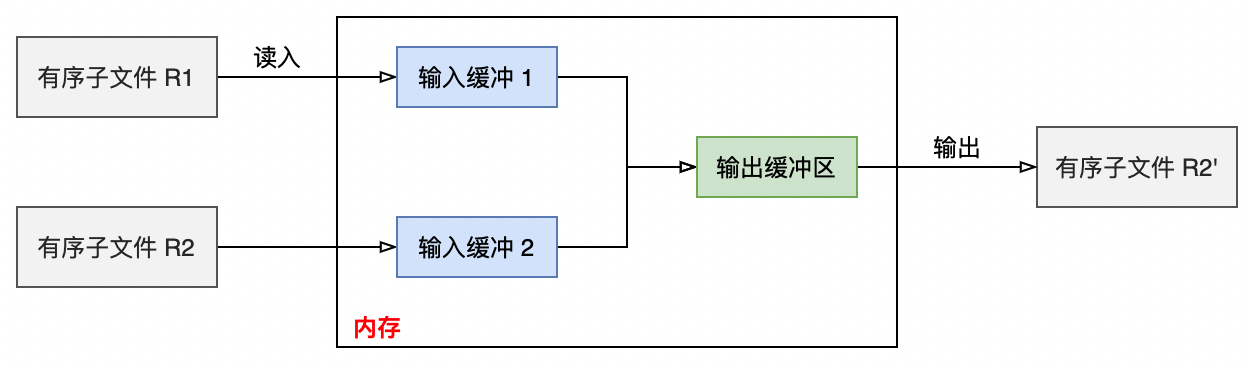
- 不断地将
的内容读入内存中的「输入缓冲区」
- 在内存中进行「归并排序」,将结果输出到「输出缓冲区」中
- 如果「输出缓冲区」写满,就将结果输出到有序子文件
中
减小磁盘读写次数
外部排序的耗时主要在「磁盘IO」上面
增大归并路数
假设:数据共 块,经过「内部排序」后形成
个有序的子文件。(共需要
次读写)
- 如果进行
路归并排序,那么需要
趟排序,共需要
次读写操作
- 如果进行
路归并排序,那么需要
趟排序,共需要
次读写操作
- 注:每一趟排序所需的读写次数是相同的
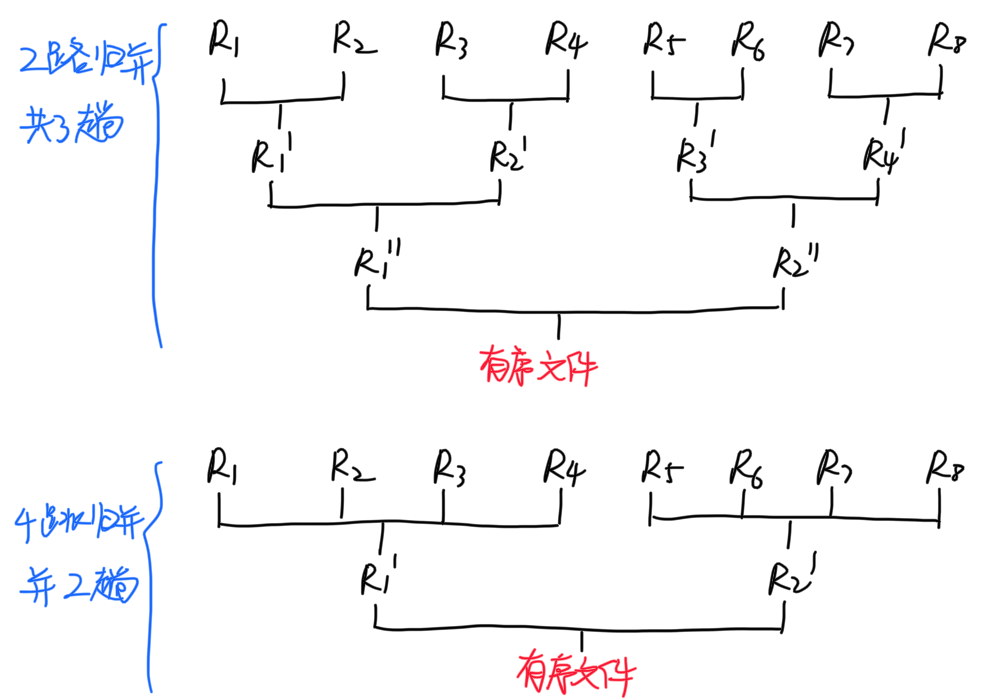
因此,增大归并的路数可以减小磁盘的 IO 次数
减小初始归并段个数
初始的归并段都是有序的,如果减小初始的归并段数量,可以减小归并的趟数,从而减小文件读写的次数。
设初始归并段数量为
,归并路数为
,则归并的趟数为
,每趟需要的文件读写次数是相同的。因此,减小初始归并段的数量,可以减小文件读写的次数。
初始归并段是有序的,通过「内部排序」得到,初始归并段的大小/数量与「内存工作区」的大小有关。
置换-选择排序
「置换-选择排序」可以得到比较大的初始归并段:
- 记初始文件为
FI,存放初始归并段的文件为FO,内存工作区为WA - 从
FI向WA中读入记录,重复以下过程:- 选出
WA中最小的记录值,记为MINIMAX,将MINIMAX输出到FO中 - 继续从
FI向WA输入记录,选择不小于MINIMAX的最小记录值输出到FO中
- 选出
- 无法再从
WA中选出比上一个MINIMAX更大的值了,表明已经得到了一个「初始归并段」。 - 重复上述过程输出更多的「初始归并段」。
注:从 WA 中选择 MINIMAX 的过程可以用「败者树」来实现。
示例:
输入文件 FI |
工作区 WA |
输出文件 FO |
说明 |
|---|---|---|---|
| 17, 21, 05, 44, 10, 12, 56, 32, 29 | - | - | 初始状态 |
| 44, 10, 12, 56, 32, 29 | 17, 21, 05 | - | FI 输入到 WA |
| 10, 12, 56, 32, 29 | 44, 17, 21 | 05 | WA 输出 MINIMAX,再从 FI 中补充一个数 |
| 12, 56, 32, 29 | 10, 44, 21 | 05, 17 | 同上 |
| 56, 32, 29 | 12, 10, 44 | 05, 17, 21 | 同上 |
| 32, 29 | 56, 12, 10 | 05, 17, 21, 44 | 同上 |
| 29 | 32, 12, 10 | 05, 17, 21, 44, 56, # | 同上。已经无法再输出 MINIMAX ,已经得到一个初始归并段 |
| - | 29, 32, 12 | 05, 17, 21, 44, 56, # 10 |
重新开始输出一个归并段 |
| - | 29, 32 | 05, 17, 21, 44, 56, # 10, 12 |
同上 |
| - | 32 | 05, 17, 21, 44, 56, # 10, 12, 29 |
同上 |
| - | - | 05, 17, 21, 44, 56, # 10, 12, 29, 32, # |
最终得到了 2 个初始归并段 |
如上述过程所示:内存工作区只能容纳 3 个记录,初始归并段的长度为 4 和 5,确实获得了更长的初始归并段。
最佳归并树
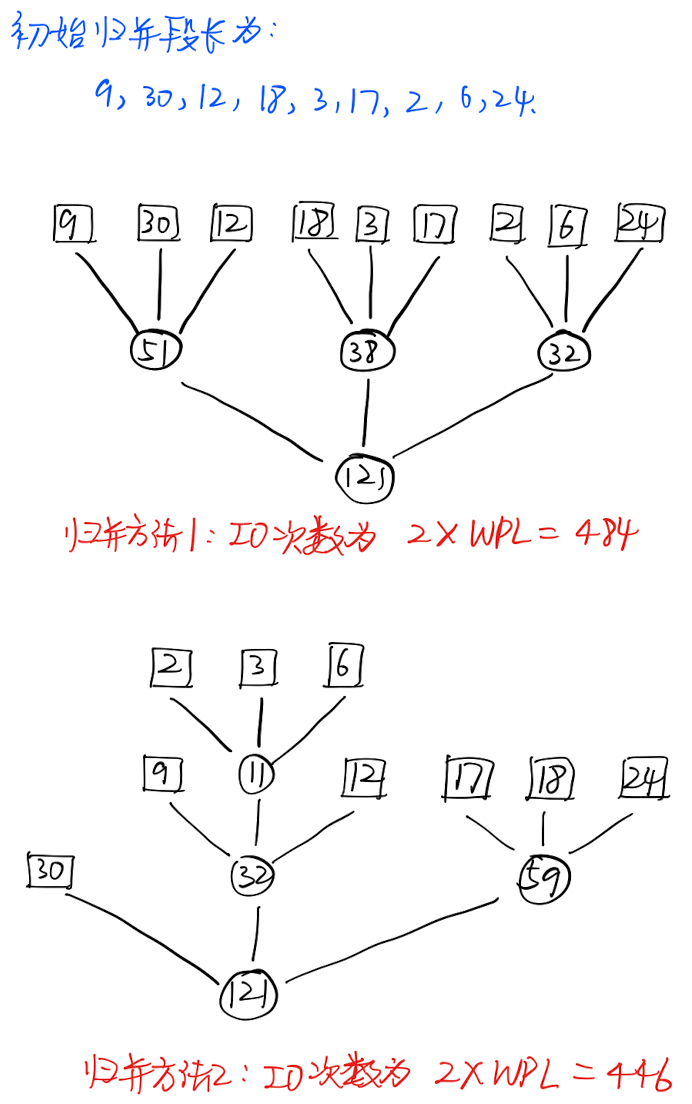
「置换-选择排序」得到的「初始归并段」长度是不同的,调整归并的顺序可以减小 IO 次数。
可以用如下的「归并树」来表示归并期间的 IO 次数:
- IO 的数量等于「归并树」的带权路径长度(除去根节点所有节点的值之和;或者叶子节点的值乘以路径长度)
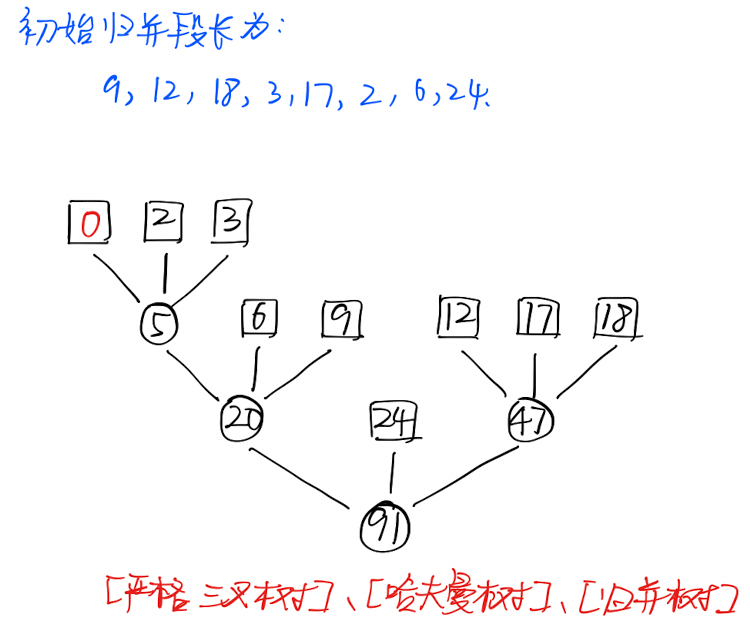
- 使用「哈夫曼树」得到的「归并树」带权路径长度最小,即「IO」次数最少
个节点是否能够构成「严格三叉树」(要么有三个字节点,要么没有字节点): 设度为 0 和 3 的节点个数分别为
,则有:
因此可以得到
,即叶子节点的数量必须是「奇数」
初始归并段可能无法构成一个「严格三叉树」,此时可以加入一个值为 的「伪节点」:
减小内部排序耗时
可以证明,如果使用普通的内部归并排序,随着归并路数的增加,内部排序总时间也会增加。
证明: 设需排序元素共
个,初始时分为
个有序子文件,归并路数为
,那么共需要
趟排序。 从
个元素中选出最小的元素,需要进行
次比较;每趟归并共需要进行
次比较。 总的比较次数为:
其中
是单增的,因此「内部排序」的耗时会随着「归并路数」的增加而增加
在 个元素中找到最小的元素,一定需要
次比较。
但是,利用「败者树」记录之前的比较结果,可以将平均每个元素的比较次数到 次,这样使得内部排序的总时间为:
,与归并路数无关。
胜者树
胜者树:叶子节点是需要比较的元素,中间节点是「胜者」的编号。
胜者树的重构:当一个元素的值发生改变时,只需要改变该元素所有「直系祖先节点」的值即可,不必改变「旁系节点」的值: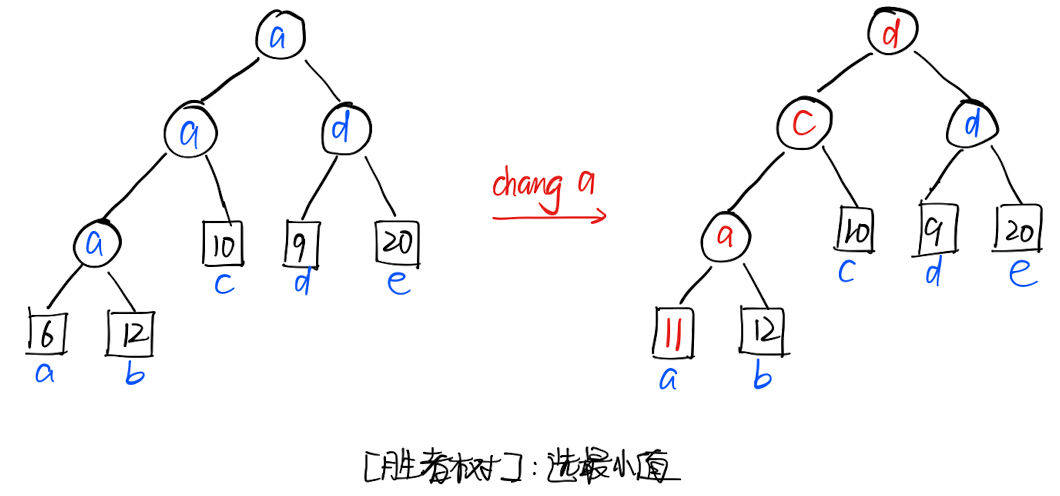
「胜者树」是一棵「完全二叉树」。利用「胜者树」,可以将每个元素的比较次数减小到 次。
败者树
败者树:叶子节点是要比较的元素,父节点记录子节点中的败者,用胜者继续比较。最后一个节点是「胜者」。
败者树的重构:当一个元素的值发生改变时,重新改变从该节点到根节点的路径上的所有节点即可。与「胜者树」的区别在于,「败者树」的重构只需要和「父节点」比较,而不需要和兄弟节点进行比较。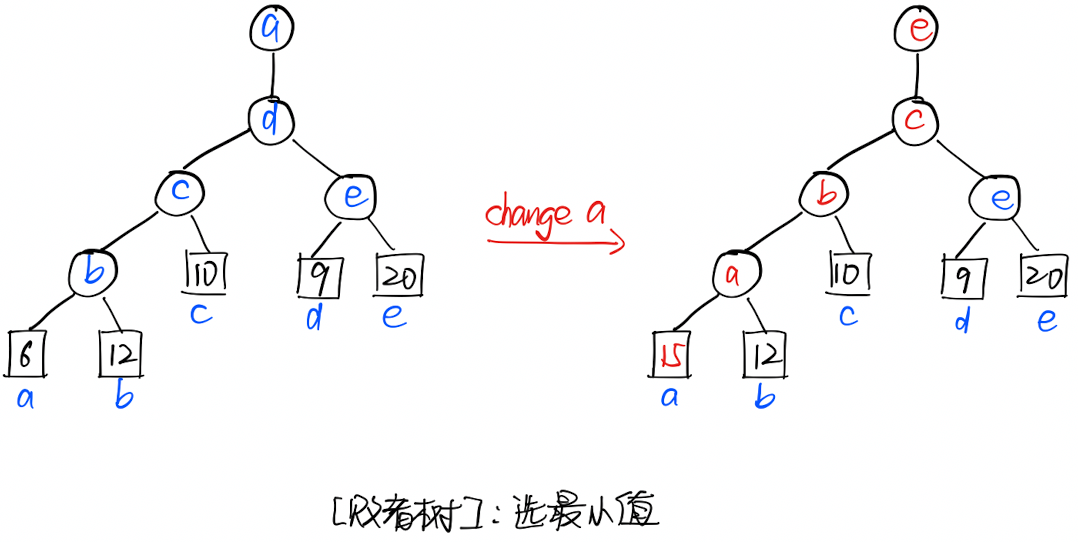
注:「胜者树」和「败者树」都只能用于「归并排序」中,无法用于普通的排序中。因为选出的都是局部的最值,由于归并排序的子序列是有序的,因此可以保证局部最值就是全局的最值。

