卡特兰数

问题的引入

问题：有 个元素要入栈出栈，入栈的顺序是固定的，现考虑「入栈-出栈的动作序列」，有多少种不同的动作序列？
例如：有 2 个元素，则可能的动作序列为：

• in-in-out-out
• in-out-in-out

为什么是卡特兰数

上述问题的答案是：

集合论的方法

「合法的动作序列」的特征
将入栈记作 +1，出栈记作 -1，则合法的「动作序列」具有以下特征：

• 动作序列的长度为
• 动作序列的和为
• 动作序列的所有前缀和都是 的，因为栈中的元素数量不能是负数

「非法动作序列」的特征
现在考虑一下非法的但是序列和仍然为 的动作序列，它们有着这样的特征：

• 一定能够找到一个前缀和是 的，因为非法的意思就是在栈中没有元素的时候仍然执行出栈操作

「和为0但非法动作序列」和「和为1的动作序列」是一一对应的
进行如下简记：

• 将「长度为的和为的非法序列」记为「序列 A」
• 将「长度为的和为的序列」记为「序列 B」

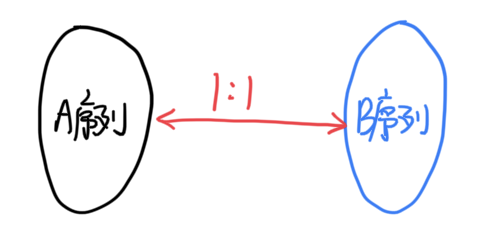
接下来证明「序列 A」和「序列 B」之间是一一映射的关系

可以找到这样一种变换，将序列 A 变换到序列 B：

• 找到序列 A 的第一个和为 的前缀，将该前缀按位取反，可以得到一个序列 B

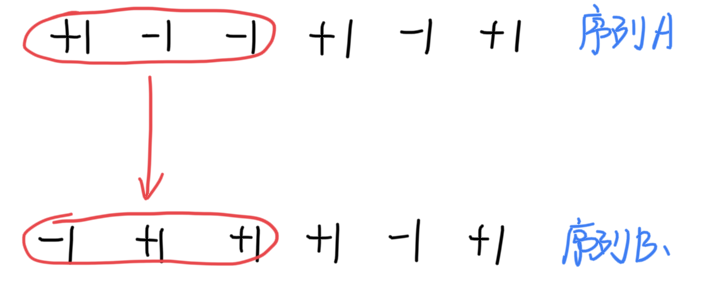
通过这样的映射变换，可以证明序列 A 和序列 B 是一一对应的，即：（反证法证明）

• 任意一个 A 都可以变换到一个 B；任意两个 A 都无法变换到同一个 B
• 任意一个 B 都可以变换到一个 A；任意两个 B 都无法变换到同一个 A

所有的合法动作序列的数量
结果是：，其中：

• 表示和为 的动作序列的数量
• 表示和为 的动作序列的数量（或和为 但非法的动作序列的数量）
• 两者相减即为和为 且合法的动作序列的数量

图示的方法

所有的入栈-出栈序列，就等价于从左上角到右下角的所有不同路径。
只能向右走或者向下走。
以abc为例：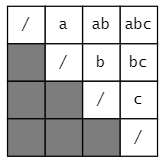

相关的问题

二叉树个数问题（没仔细看这个）

问题描述：
求叶子数为 的不同二叉树共有多少种，要求二叉树结点要么没有子，要么有两个子：
问题求解：
可以使用向左优先的深度优先遍历，得到一个序列 。
叶子数为 的二叉树的遍历序列有一个特点：前缀和必为非负数，序列总和为 。
可以使用卡特兰数求解。