红黑树的性质
红黑树必须满足的性质:
- 每个节点要么是「红色」,要么是「黑色」
- 根节点必须是「黑色」
- 叶子节点是「黑色」(叶子节点是 「NIL」,里面没有关键字)
- 「红色」节点的子节点必须是「黑色」节点
- 从根节点到任意叶子节点,路径上「黑色」节点的数目相同。即,任意叶子的「黑色高度」相同。
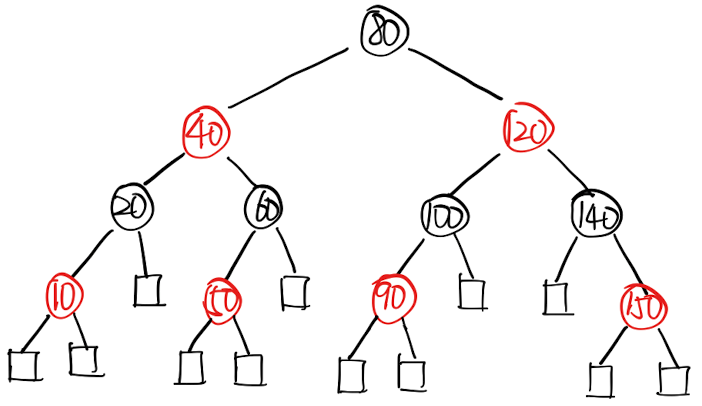
红黑树与B树
红黑树实际上就是 「3阶B树」或者「4阶B树」
节点之间的相互转化: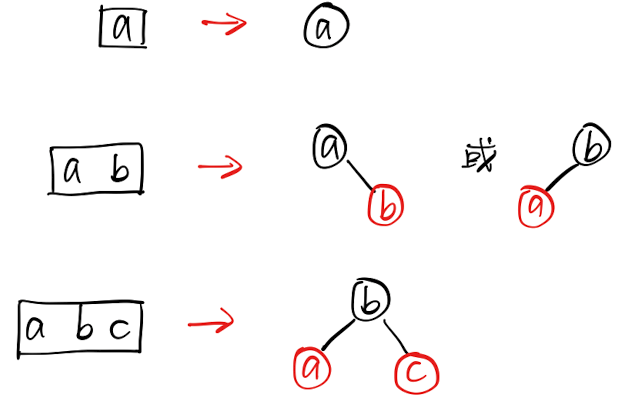
从上图可以看出:「红色节点」是「黑色节点」的附属。
「红黑树」的黑色高度相同,意味着什么:因为「B树」是严格平衡的,每一个「B树节点」都可以且只能转化为一个「黑色节点」。因此,黑色高度相等正是「B树」平衡的体现。
「4阶B树」转化为「红黑树」: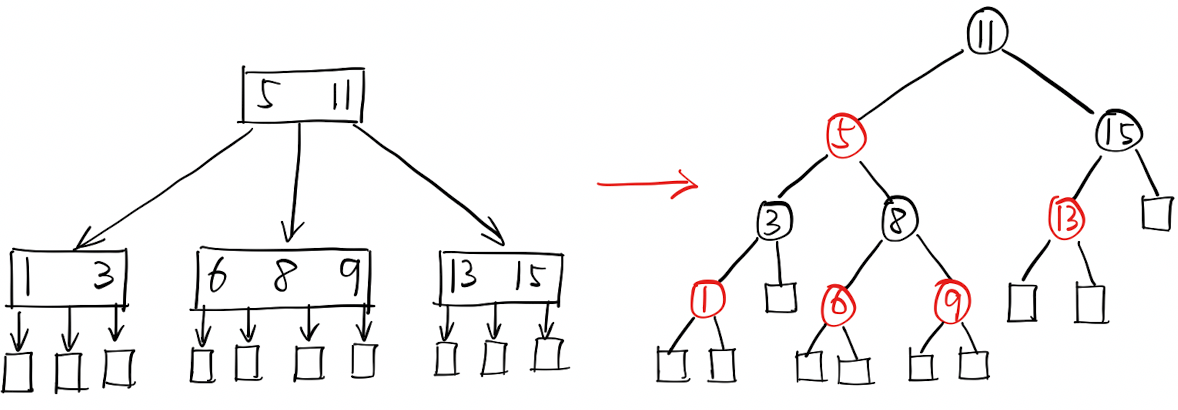
开头的「红黑树」转化为「B树」: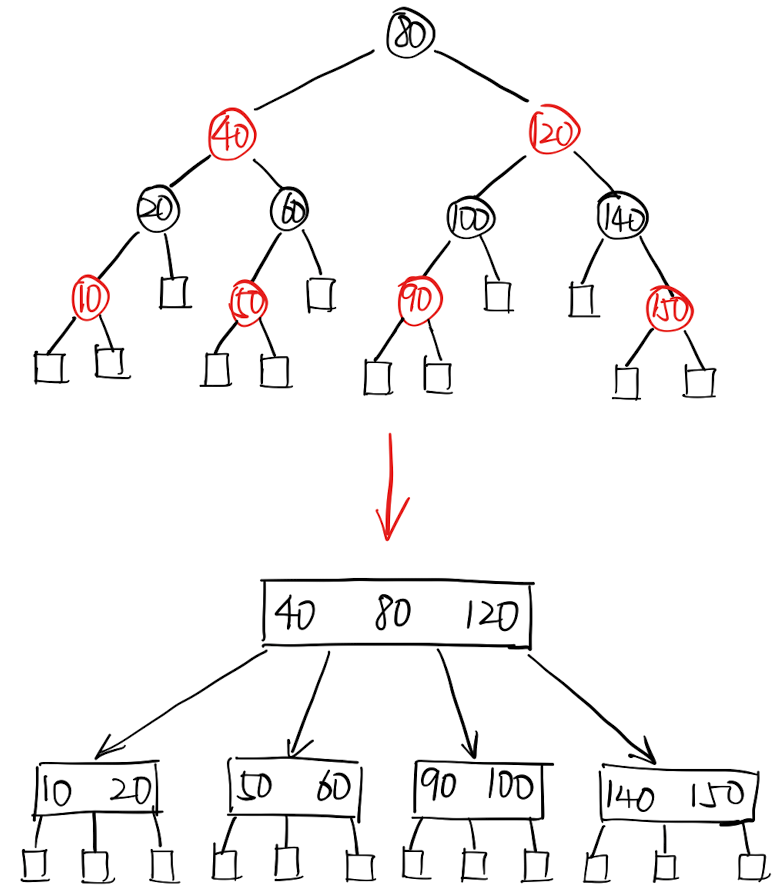
插入元素
整体思路为:先变颜色,再进行旋转操作。会发现,不满足性质的部分会从底层逐渐上升到根部去。
情形1:插入根节点
新插入的节点是根节点:将该节点标记为「黑色」
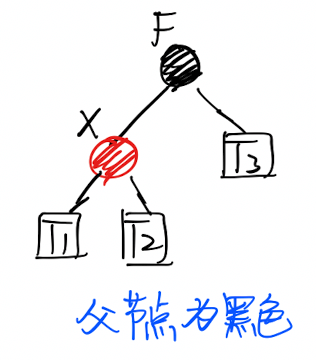
情形2:父节点为黑色
情形3:父节点为红色
3-1:父节点红色,叔节点红色
父节点是「红色」,叔节点是「红色」
- 将父节点和叔节点设为「黑色」,祖父节点设为「红色」
- 继续处理祖父节点
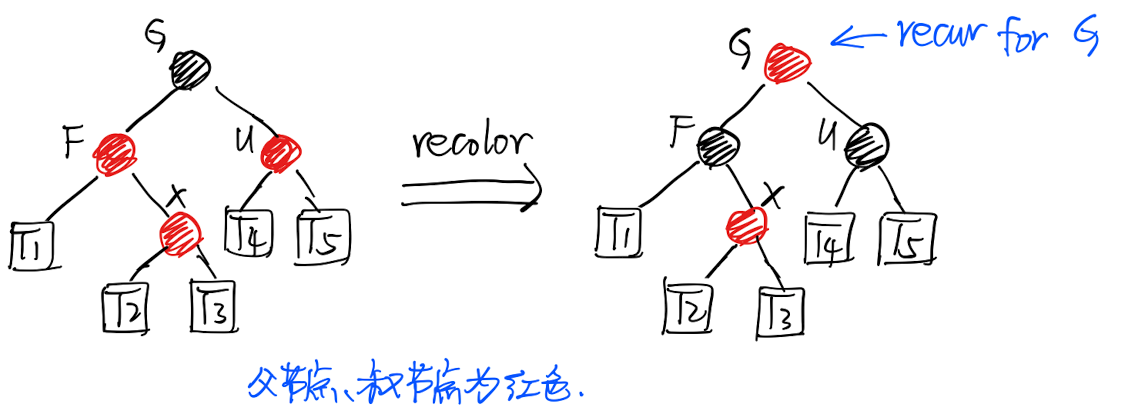
从「B树」的角度来理解: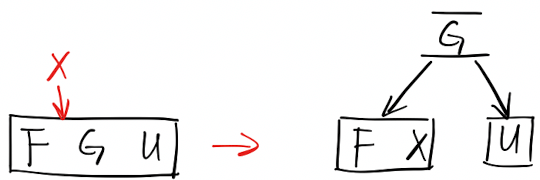
3-2:父节点红色,叔节点黑色
「LL」(或对称的「RR」)情形:
- 对祖父节点进行右旋操作
- 改变父节点和祖父节点的颜色
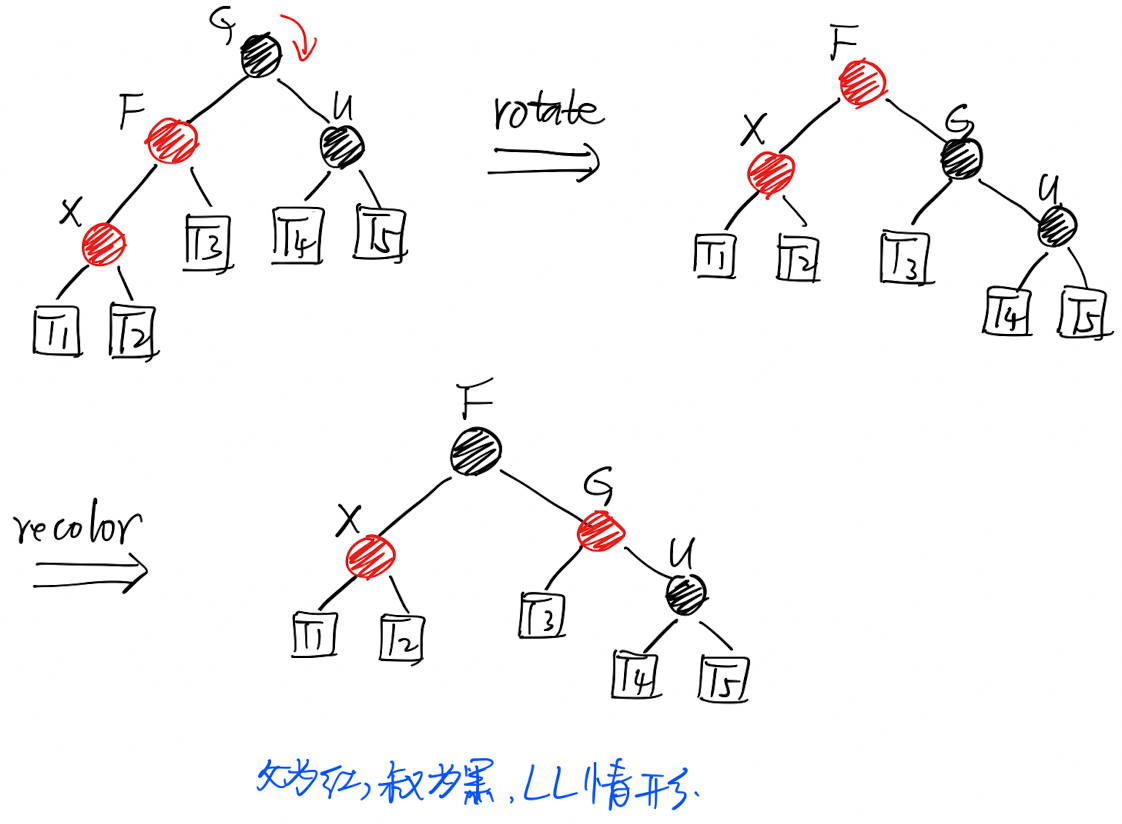
从「B树」的角度来理解:
「LR」情形(或对称的「RL」情形):
- 对父节点进行左旋操作
- 问题归结为「LL」情形(或「RR」情形)
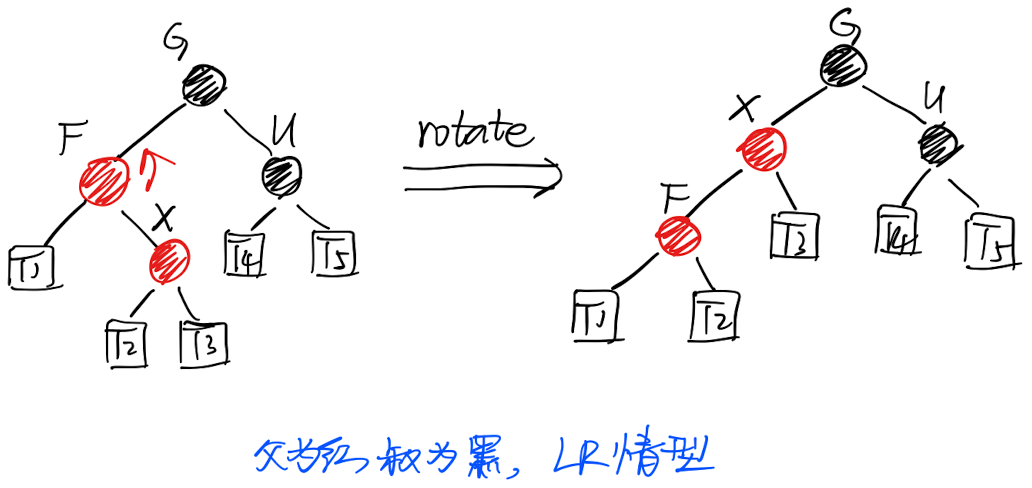
从「B树」的角度来理解: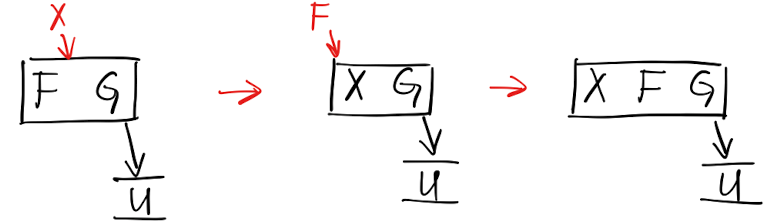
删除元素
删除可以分为两个步骤:
- 按照「二叉排序树」的情形,删除节点
- 对树进行调整,使之符合「红黑树的」特征
按照「二叉排序树」的情形删除节点:
- 情形1:如果没有子节点,那么直接删除
- 情形2:如果有一个字节点,那么用子节点替代被删除的节点
- 情形3:如果有 2 个子节点,那么使用其后继来替代被删除的节点
上述情形最终都可以转换为「情形1」: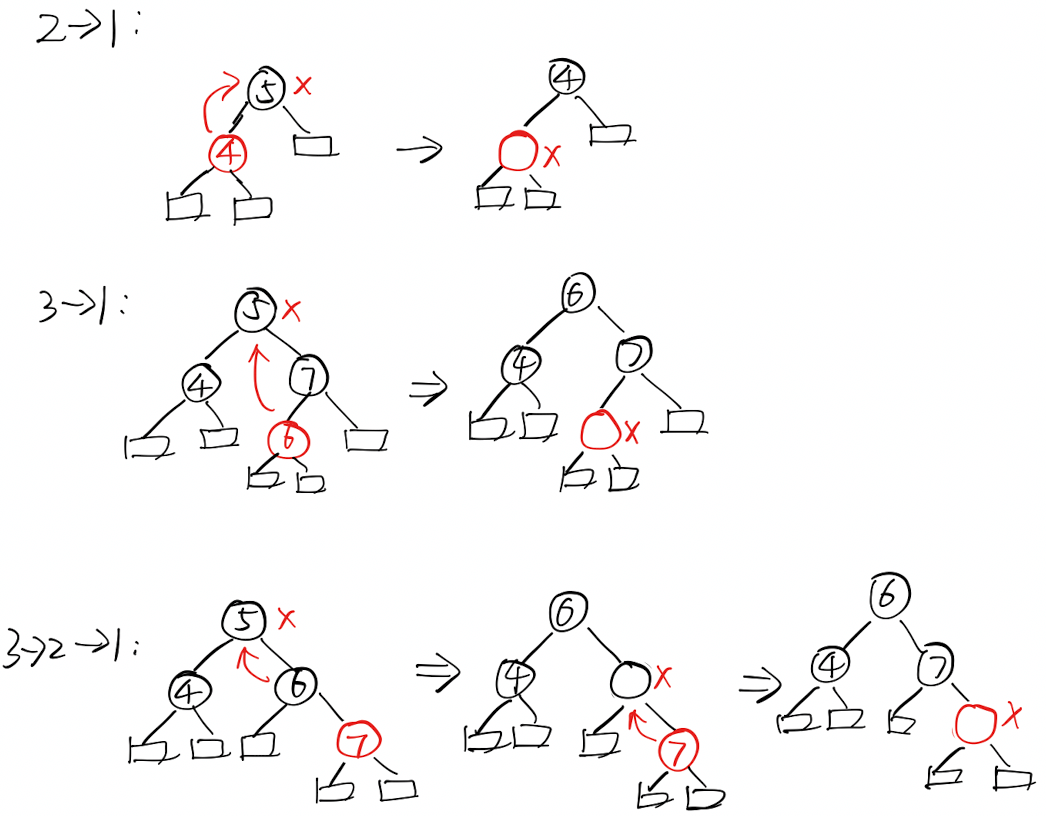
最终问题可以归结为:删除最下方的一个节点
情形1:如果节点是红色的
如果节点是红色,直接删除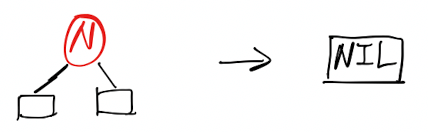
情形2:如果节点是黑色的
节点是黑色,且为左子(右子情况是对称的)
| 情形编号 | 情形描述 | 如何处理 | |
|---|---|---|---|
| 2.1 | 兄弟节点为黑色 | 兄弟的右子为红色 | 直接解决 |
| 2.2 | 兄弟的左子为红色 | 可以转化为 2.1 | |
| 2.3 | 兄弟的左右子都为黑色 | 继续处理父节点,转化为 2.1~2.4 | |
| 2.4 | 兄弟节点为红色 | 可以转化为 2.3 |
2.1 兄弟为黑色,其右子为红色
- 兄弟节点和父节点交换颜色,兄弟的右子变为黑色
- 父节点左旋
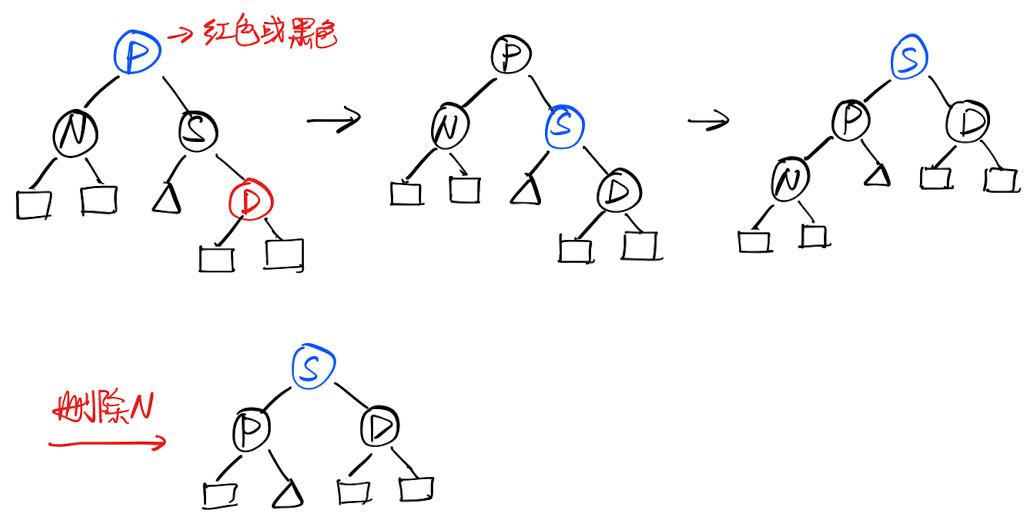
从「B树」的角度来理解: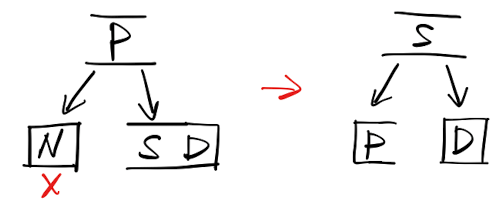
2.2 兄弟为黑色,其左子为红色
- 兄弟变为红色,兄弟的左子变为黑色
- 兄弟右旋
- 问题转化为 2.1
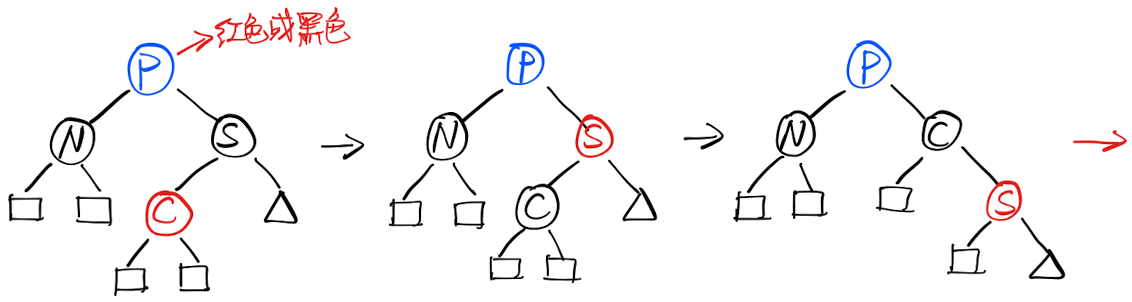
从「B树」的角度来理解: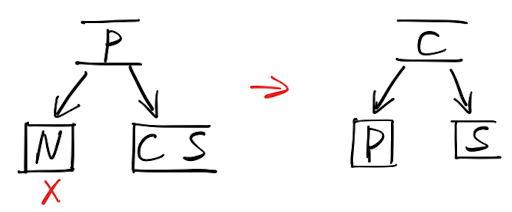
2.3 兄弟为黑色,其左右子都是黑色
- 兄弟节点设为红色
- 假设父节点是需要删除的节点,继续处理
- 最终删除的时候,删除的是当前节点,并将父节点变为黑色。
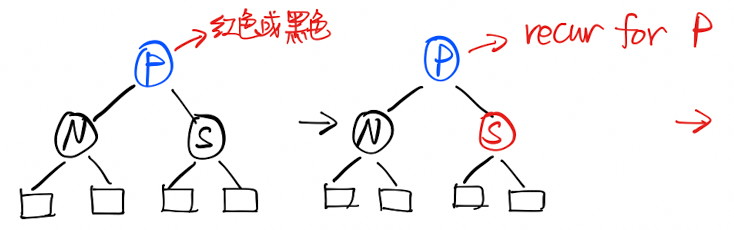
2.4 兄弟为红色
- 父节点变为红色,兄弟节点变为黑色
- 左旋父节点
- 问题转化为 2.3。
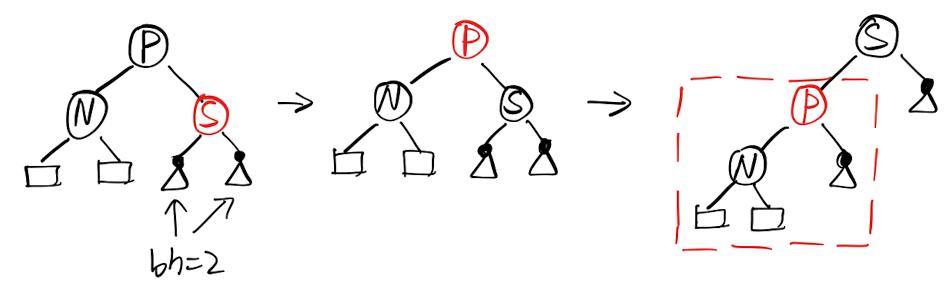
从「B树」的角度来理解(情形 2.3 和 2.4):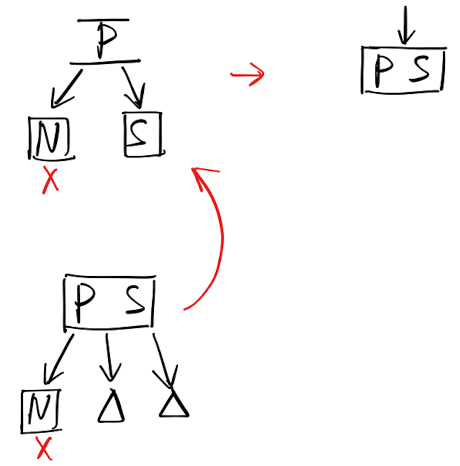
TODO: 如何检验学习成果: 在一个序列上手工构建红黑树,然后手工删除某些元素,和参考结构做对比 序列:【10 70 32 34 13 56 32 56 21 3 62 4】 在线红黑树:https://rbtree.phpisfuture.com