依靠的性质：两点之间的最短路径，包含了路径上其他顶点之间的最短路径。

对于非带权图，可以利用广度优先搜索 BFS 来得到单源最短路径。

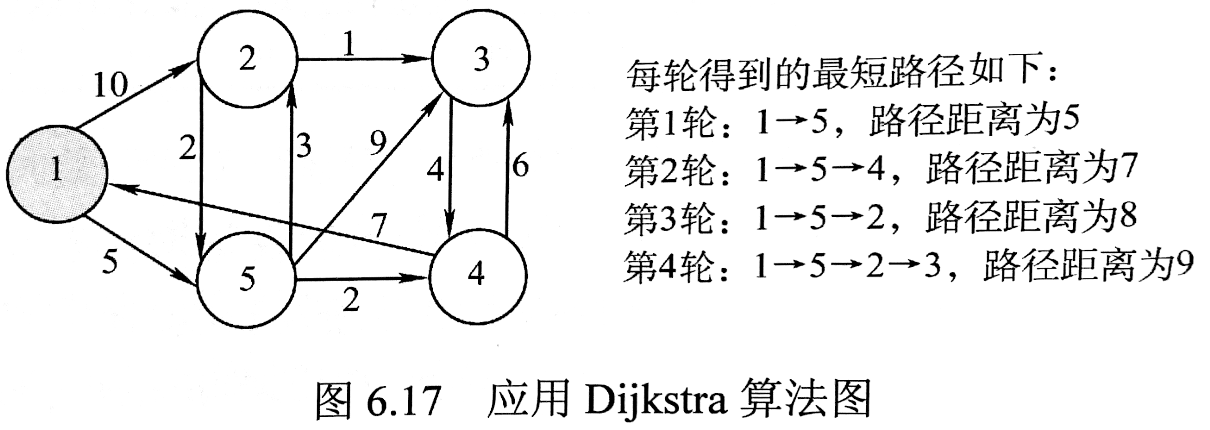
单源最短路径：Dijkstra算法（贪婪）

辅助数据结构：
  • solved[]：标记一个顶点是否已经被解决
  • distance[]：表示从源点到某一点的最短路径长度。每当找到一个新的节点的最短路径的适合，就更新这个数据结构。
  • **path[]**：结点在最短路径上的前趋结点，类似于树的双亲表示法

image.png

「Prim算法」和「Dijkstra算法」的比较：

  • 在「Prim算法」中，distance[] 中存放的是从生成树到某个结点的最短边长
  • 在「Dijkstra算法」中，distance[] 中存放的是从源点到结点的最短路径长度

局限性：当图中具有负权值的边时，「Dijkstra算法」失效。

注：单源最短路径得到的生成树并不一定是最小生成树。

多源最短路径：Floyd算法

本质是 DP
每次迭代的时候，多考虑一个顶点进去。
迭代过程如下：

  1.     ![](https://cdn.nlark.com/yuque/__latex/df8a1017e3e8d457dfc4b94c91c6c536.svg#card=math&code=A%5E%7B%28-1%29%7D%5Bi%5D%5Bj%5D%3Darcs%5Bi%5D%5Bj%5D&height=23&id=BVYfH)
  3.     ![](https://cdn.nlark.com/yuque/__latex/cbfa17f8406bce1242bb49e9a9dd9f4a.svg#card=math&code=A%5E%7B%28k%29%7D%5Bi%5D%5Bj%5D%3DMin%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Blll%7DA%5E%7B%28k-1%29%7D%2C%5C%5C%20A%5E%7B%28k-1%29%7D%5Bi%5D%5Bk%5D%2BA%5E%7B%28k-1%29%7D%5Bk%5D%5Bj%5D%5Cend%7Barray%7D%5Cright.&height=47&id=wZDJG)

其中：

  • 最短路径 - 图2 表示从 最短路径 - 图3 到 最短路径 - 图4 的直接距离
  • 最短路径 - 图5 表示考虑中间顶点 最短路径 - 图6 后，最短路径 - 图7 到 最短路径 - 图8 的距离

局限性：可以处理带负权值的图；不允许带负权值的边组成回路。

如何理解 Floyd 算法：

  • 最短路径 - 图9 表示利用了 最短路径 - 图10 节点后 最短路径 - 图11 节点之间的最短距离。
  • 转移方程就是上面的方程。