多源 BFS

题目

有一张矩形的地形图，每个格子都有一个高度值。

• 如果格子中是水，那么高度值必须是 0；
• 高度值是非负的；
• 相邻格子（左右或上下相邻）之间高度值最多相差 1；

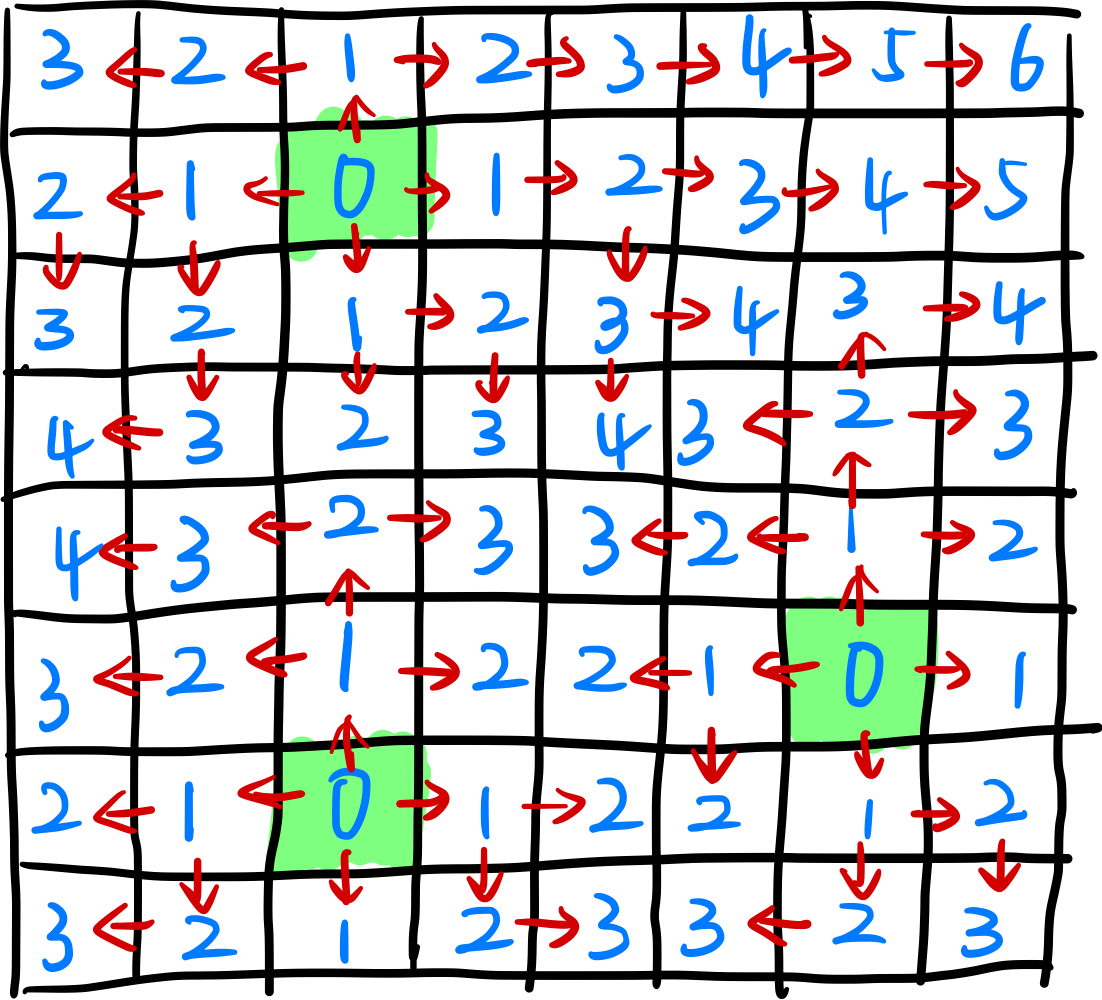
给定地形图上水源的位置，为地形图填入高度，使得地形图中最高高度的格子尽可能高。

例如：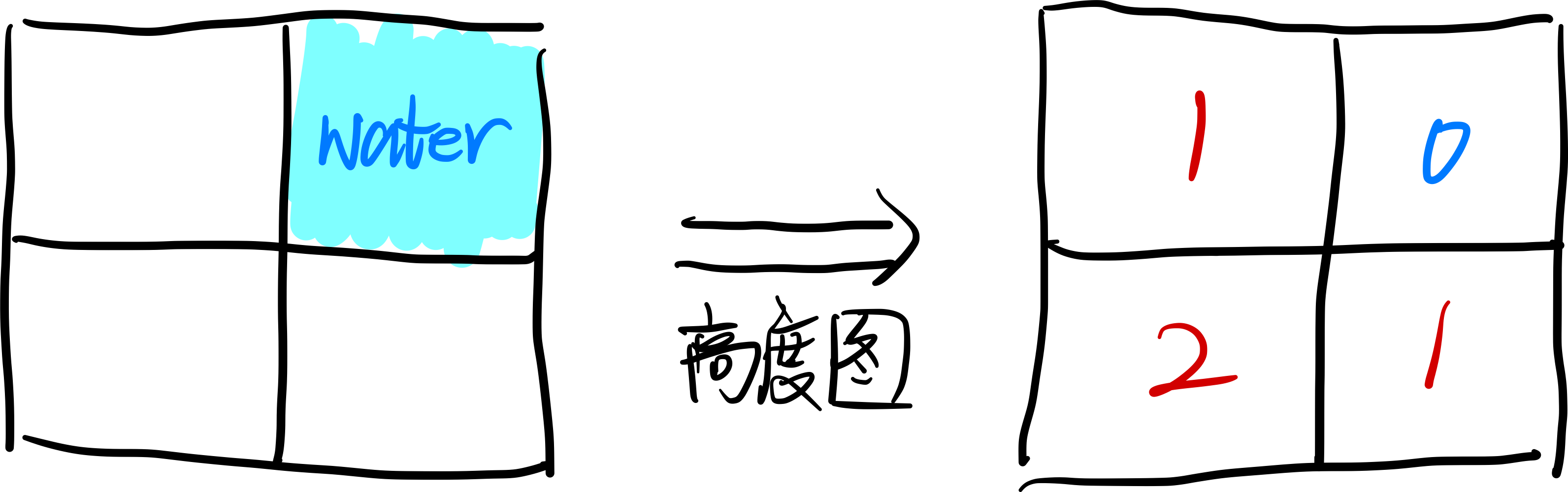

分析

某个格子的最高高度，取决于到水源的最近距离（曼哈顿距离）。

最直观的想法是：对于地图上的每个格子，遍历所有的水源，计算最小的距离，该格子的高度就是最小距离。这样做的时间复杂度为 ，其中 是水源的数量。如果地图中的水源太多，时间复杂度会较大。
或许可以在水源上建立加速结构，例如四叉树之类的结构。

另一种思路是：对于地图上的每个水源，同时向外扩散，每扩散一圈，高度就增加 1。

可以用一个队列来加速这种计算，减少很多的重复判断。每个格子只需要处理邻近的四个格子：

前进中的波，波前上的每一点都可以看出新的波源。