模式串匹配问题

题目

判断模式字符串p是否能匹配字符串s
模式字符串包含以下
    '.' 匹配任意单个字符
    '*' 匹配零个或多个前面的那一个元素
输入:
    s = "aab"
    p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

解题

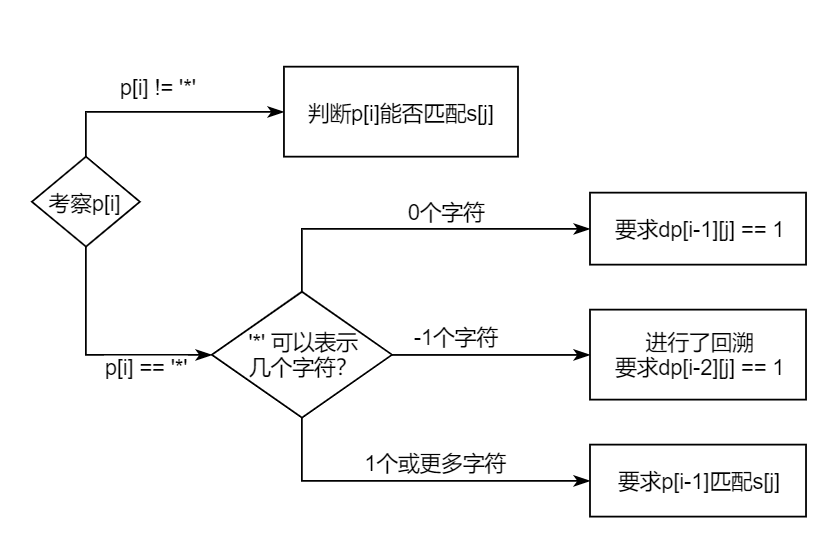
：由于`x*`合起来可以表示0个或多个`x`字符，所以`*`字符可以取消前一个字符的匹配，这就有了回溯。<br />    模式串`p[0...i]`是否能够匹配字符串`s[0...i]`？可以从`p[0...i-1]`的匹配情况判断：

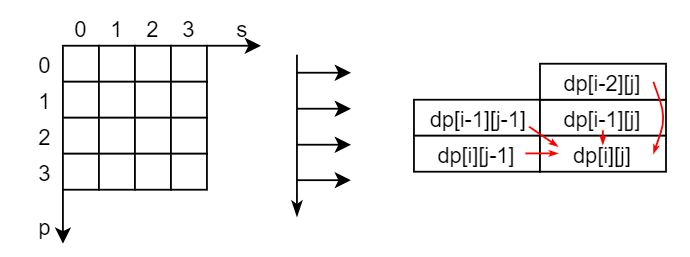
设计dp[i][j]表示模式串p[0...i]是否能够匹配字符串s[0...j] ##

题目描述

给定一个字符串 (s) 和一个字符模式 (p) ，实现一个支持 '?' 和 '*' 的通配符匹配。
    '?' 可以匹配任何单个字符。
    '*' 可以匹配任意字符串（包括空字符串）。
说明:
    s 可能为空，且只包含从 a-z 的小写字母。
    p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

解题

最优子结构

p[0...i]要能够匹配s[0...j]：

• 如果p[i]是'?' , 那么必有 dp[i - 1][j - 1] == 1

• 如果 p[i] 是一般字符, 且p[i] == s[j]，那么必有 dp[i - 1][j - 1] == 1

• 如果p[i] 是 '*', 那么：

• *表示0个字符，必有 dp[i - 1][j] == 1

• *表示1个字符，必有 dp[i - 1][j - 1] == 1
• *表示多于1个字符，必有 dp[i][j - 1] == 1

空间优化：

只需要两行即可：第i行和第i-1行；在每次循环时即可。

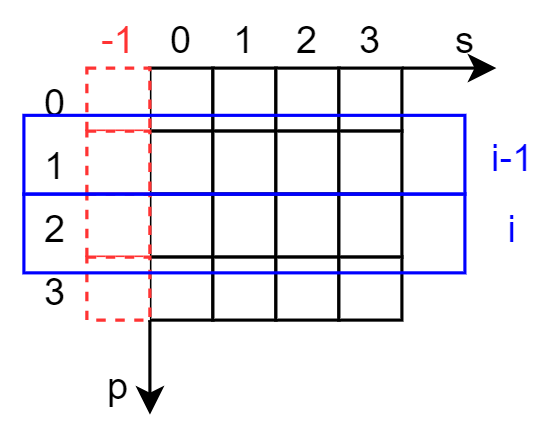
初始化的优化：

初始化第一列时十分不方便，可以多增加一列：dp[i][-1]，表示模式p[0...i]能够匹配空字符串，只有模式串全部为'*'时才能匹配成功。 通配符匹配.cpp