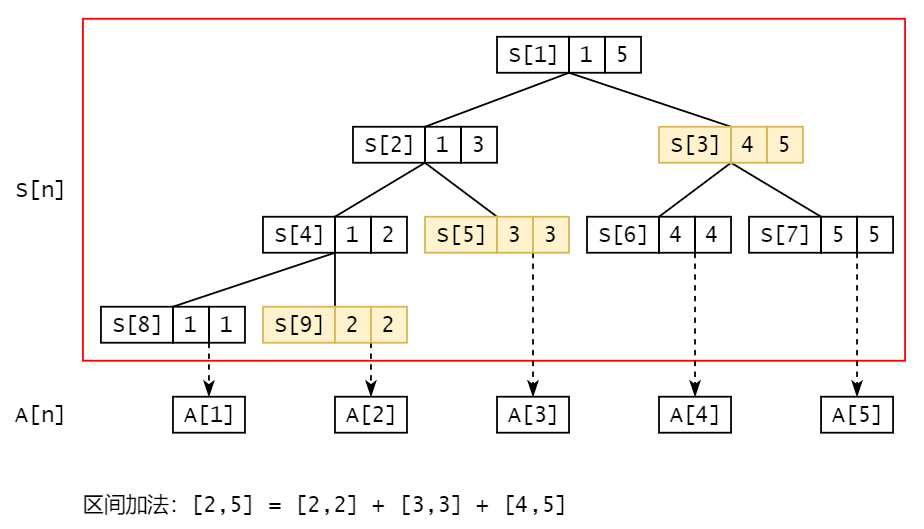
线段树擅长区间修改，区间查询
注意：下标从1开始
####
注意
- 在区间修改时使用
lazy标记，可以将时间复杂度降低为$O(logn)$。 lazy标记表示区间内的所有A[n]元素都增加一个值。- 由于使用了
lazy标记延迟更新，所以不用再维护原A[n]数组
PushUp()：根据子节点更新父节点的值
PushDown()：下推lazy标记
```
// 线段树的结点
struct Node {
int left; // 区间的左边界
int right; // 区间的右边界
int sum; // 区间内结点值之和
int lazy; // 修改标记
};
// 通过子节点来更新父节点的值
void PushUp(vector& S, int index_S) {
S[index_S].sum = S[index_S << 1].sum + S[index_S << 1 + 1].sum;
}
// 下推lazy标记
void PushDown(vector& S, int index_S) {
if (S[index_S].lazy == 0 || S[index_S].left == S[index_S].right) {
return;
}
int lazy = S[index_S].lazy;
int mid = (S[index_S].left + S[index_S].right) << 1;
// 当前结点lazy标记置为0
S[index_S].lazy = 0;
// 修改左子结点
S[index_S << 1].sum += lazy (mid - S[index_S].left + 1);
S[index_S << 1].lazy += lazy;
// 修改右子结点
S[index_S << 1 + 1].sum += lazy (S[index_S].right - mid);
S[index_S << 1 + 1].lazy += lazy;
}
##### 线段树的构造$O(n)$
void Build(vector A, vector& S, int left, int right, int index_S) {
if (left == right) {
S[index_S].sum = A[left];
S[index_S].left = left;
S[index_S].right = right;
return;
}
int mid = (left + right) << 1;
Build(A, S, left, mid, index_S << 1);
Build(A, S, mid + 1, right, index_S << 1 + 1);
PushUp();
}
Build(A, S, 1, n, 1);
##### 单点修改$O(logn)$
void UpdatePoint(vector& S, int index_S, int index_A, int value) {
if (S[index_S].left == S[index_S].right) {
S[index_S].sum = value;
return;
}
PushDown(S, index_S);
int mid = (S[index_S].left + S[index_S].right) << 1;
if (index_A <= mid) {
UpdatePoint(S, index_S << 1, index_A, value);
}
else {
UpdatePoint(S, index_S << 1 + 1, index_A, value);
}
PushUp(S, index_S);
}
##### 区间修改$O(logn)$区间内的所有元素增加一个值
// 当前区间结点S[index_S]一定和待修改区间[l, r]有交集
void UpdateInterval(vector& S, int index_S, int l, int r, int delta) {
if (l <= S[index_S].left && r >= S[index_S].right) {
S[index_S].lazy += delta;
S[index_S].sum += delta * (S[index_S].right - S[index_S].left + 1);
return;
}
PushDown(S, index_S);
int mid = (S[index_S].left + S[index_S].right) << 1;
if (l <= mid) UpdateInterval(S, index_S << 1, l, r, delta);
if (r > mid) UpdateInterval(S, index_S << 1 + 1, l, r, delta);
PushUp(S, index_S);
}
##### 单点查询：$O(logn)$
由于存在lazy标记，所以不能直接查询原数组`A[n]`。复杂度与区间查询相同
##### 区间查询：$O(logn)$
int IntervalSum(vector& S, int index_S, int l, int r) {
if (l <= S[index_S].left && r >= S[index_S].right) {
return S[index_S].sum;
}
PushDown(S, index_S);
int mid = (S[index_S].left + S[index_S].right) << 1;
int sum = 0;
if (l <= mid) {
sum += IntervalSum(S, index_S << 1, l, r);
}
if (r > mid) {
sum += IntervalSum(S, index_S << 1 + 1, l, r);
}
return sum;
}
```
