树状数组

🌲树状数组

树状数组擅长单点修改，区间查询

在原数组A[n]的基础上构建一个辅助数组，记作C[n]。

🍃

• 它表示：一个数用二进制表示时，最低位的1所表示的值。
• 另一重含义：它表示一个数的最大因数，这个因数必须是2的k次幂。
• 计算lowBit的方法：lowBit = i&(-i)。原理：补码，取反加一。
• 比如：
• 24：二进制表示为11000，lowBit = 8。
• 12：二进制表示为1100，lowBit = 4。

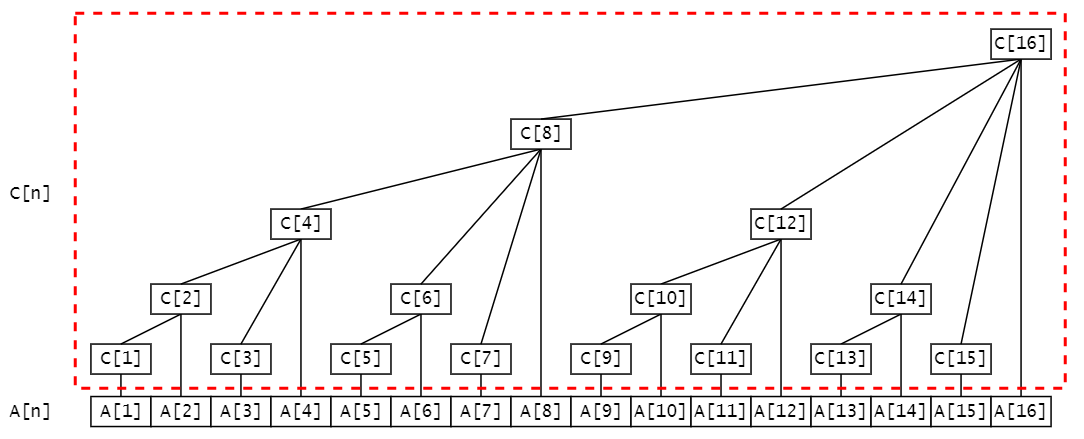##### 🍃 C[i]的含义

• C[i]表示：数组A[n]中，包括A[i]在内的前方lowBit个元素的总和。

$$
C[i] = \sum_{t=0}^{lowBit}A[i-t]
$$

• C[i]还可以使用数组C[n]中的其他元素来表示：
• 对于i来说：$2^k = lowBit$；i的二进制表示中，末尾有k个0；C[i]表示A[n]中$2^k$个元素的和；
• ，对于$i-2t]$表示A[n]中$2^t$个元素的和；
• $2k=1+\sum_{t=0}t$，所以C[i]可以用其他的C[n]表示为：

$$
C[i] = A[i] + \sum_{t=0}^{k - 1}C[i-2k=lowBit
$$

🍃 父子结点

• C[i]的父节点是C[i+lowBit]。
• C[i]的子节点共有k + 1个，其中$2^k = lowBit$。

  🍃 构造$O(nlogn)$

  通过C[i]的子节点来构造C[i]，复杂度是$O(nlogn)$。 ``` void Init(vector A, vector C) { for (int i = 1; i < A.size(); ++i) {

    int lowBit = i & (-i);
    C[i] = A[i];
    for (int pf = 1; pf < lowBit; pf <<= 1) {
        C[i] += C[i - pf];
    }

  } }

##### 🍃 单点查询$O(1)$
直接查询`A[n]`即可，所以复杂度为$O(1)$。
##### 🍃 区间查询$O(logn)$

// 计算区间和，闭区间C[a, b] int IntervalSum(vector C, int a, int b) { return PrefixSum(C, b) - PrefixSum(C, a - 1); } // 计算前缀和，闭区间A[1, m] int PrefixSum(vector C, int m) { int sum = 0; while (m > 0) { sum += C[m]; m -= (m & (-m)); } return sum; }

##### 🍃 单点修改$O(logn)$
找到所有的祖先结点即可，复杂度为$O(logn)$。

void Update(vector& A, vector& C, int index, int value) { int delta = value - A[index]; A[index] = value; // 受影响的结点都增加delta即可 while (index < c.size()) { c[index] += delta; index += (i & (-i)); // 定位到父节点 } }

```

🍃 区间修改x

并不擅长