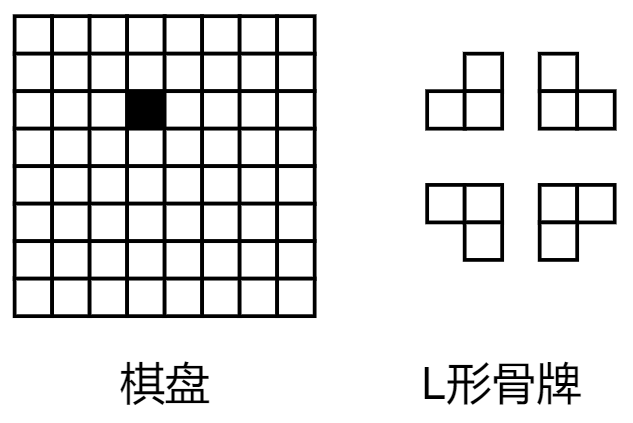
问题描述

在一个 棋盘覆盖问题 - 图1 个方格组成的棋盘中，有一个方格称为特殊方格。 使用以下四种L型骨牌覆盖棋盘上除特殊方格外的所有方格，且不能重叠。 棋盘覆盖问题 - 图2

解题

首先考虑 棋盘覆盖问题 - 图3 的情形：
答案明显，非常清晰
再考虑 棋盘覆盖问题 - 图4 情形：
将整个棋盘分成4格部分。
有特殊方格的那个部分，容易解决；
没有特殊方格的其他三个子棋盘，可以通过加入一个横跨三个子棋盘的骨牌，将问题转化为 棋盘覆盖问题 - 图5 规模。
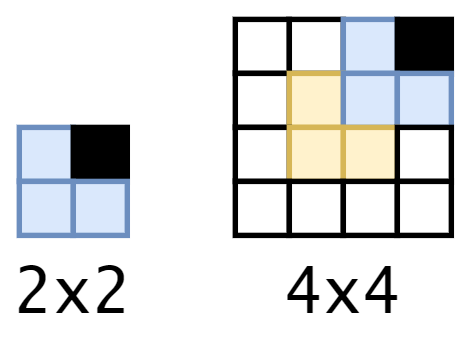
棋盘覆盖问题 - 图6
这样推广到 棋盘覆盖问题 - 图7 情形即可。

  1. struct ChessBoard {int x, y, size};
  2. strcut Cell {int x, y};
  3. void Cover(ChessBoard b, Cell c) {
  4.     // 基准情形
  5.     if (b.size == 2) {
  6.         // 输出结果
  7.         return;
  8.     }
  9.     // 需要划分的情形
  10.     int midX = b.x + size >> 1;
  11.     int midY = b.y + size >> 1;
  12.     int quadrant = 0;            // 标记特殊方格位于第几象限
  13.     if (c.x < midX) {
  14.         if (c.y < midY) {
  15.             // 判断象限，求解包含特殊方格的子棋盘的子问题
  16.             quadrant = 3;
  17.             Cover({b.x, b.y. size >> 1}, c);
  18.             // 放置一个相应形状的L形骨牌在中间
  19.         }
  20.         else {
  21.             quadrant = 2;
  22.             Cover({b.x, midY, size >> 1}, c);
  23.             // ...
  24.         }
  25.     }
  26.     else {
  27.         if (c.y < midY) {
  28.             quadrant = 4;
  29.             ...
  30.         }
  31.         else {
  32.             quadrant = 1;
  33.             ...
  34.         }    
  35.     }
  37.     // 求解没有特殊方格的剩余3格子棋盘的子问题
  38.     if (quadrant != 1)
  39.         Cover({midX, midY, size >> 1}, {midX, midY});
  40.     if (quadrant != 2)
  41.         Cover({b.x, midY, size >> 1}, {midX - 1, midY});
  42.     if (quadrant != 3)
  43.         Cover({b.x, b.y, size >> 1}, {midX - 1, midY - 1});
  44.     if (quadrant != 4)
  45.         Cover({midX, b.y, size >> 1}, {midX, midY - 1});
  46. }