哈夫曼树

带权路径长度：根节点到当前节点的长度，乘以当前节点的权值。
所有叶子节点的带权路径长度之和，即为树的带权路径长度：
哈夫曼树：树的带权路径长度最小

哈夫曼树的特征：由于哈夫曼树中只存在度为 0 和度为 2 的节点，因此叶子节点数量比非叶子节点数量多 1。

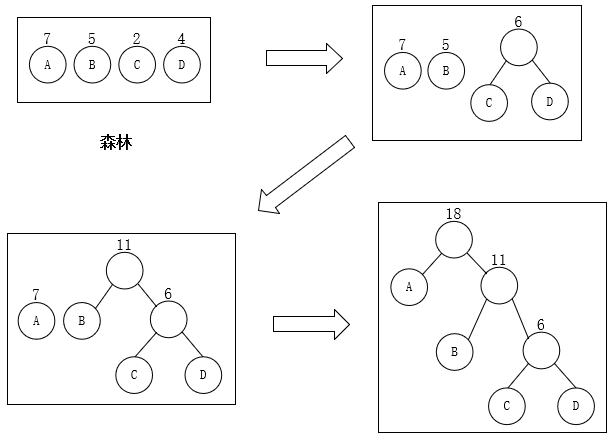
哈夫曼树的构造

哈夫曼树的构造

• 初始时所有结点单独为一棵树，共同构成森林
• 不断将权值最小的树合并在一起

哈夫曼编码

可变长度编码：在数据通信中，字符用二进制位表示。如果表示每个字符的二进制位长度不全相同，则这种编码成为可变长度编码。
前缀编码：如果不存在一个字符的二进制编码是另一个字符的二进制编码的前缀，则称这种编码方式为前缀编码。只要字符位于二叉树的叶子节点，得到的编码就是前缀编码。

哈夫曼编码：是一种可变长度编码，也是前缀编码。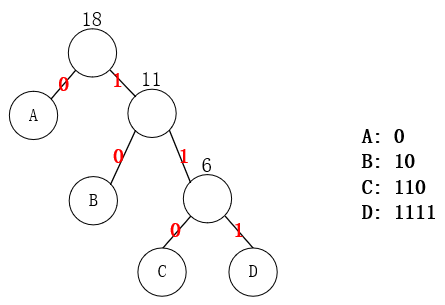

哈夫曼编码的数量关系：高度为 的哈夫曼树的总节点数最多为 ，即满二叉树。