线索二叉树

链式二叉树具有 个空链域，利用这些空链域来标记树节点在遍历时的前驱和后继，这样就可以像遍历链表一样遍历二叉树了。
线索二叉树可以加快查找节点的前驱和后继的速度。

线索二叉树的结构

以中序为例
如果一个节点没有左子，就将左子指向前驱；如果没有右子，就使用右子指向其后继
如下图所示：

• 该二叉树中序遍历的结果为： DGBAECF
• 根据中序遍历的结果建立「线索」

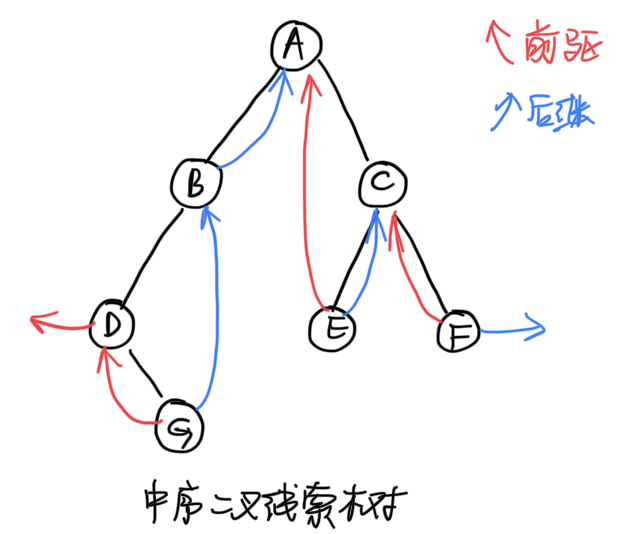
为了区分链域中是指向子节点还是前驱/后继节点，还要引入标志位

有多少个指向 **Null** 的线索：（指向 Null，意味着没有前驱或后继，同时也没有左子或右子）

• 中序线索二叉树：
  • 第一个节点是最左边的节点，一定没有左子，前驱线索为 Null
  • 最后一个节点是最右边的节点，没有右子，后继线索为 Null
• 前序遍历二叉树：
  • 第一个节点是根节点，如果没有左子的话，那么前驱线索为 Null
  • 最后一个节点一定是叶子节点（叶子节点中最右边一个），后继线索为 Null
• 后序遍历二叉树：于前序类似

建立线索二叉树

前驱和后继关系来自于遍历中，所以应当在遍历过程中将二叉树「线索化」

建立方法：

• 如果当前节点没有左子节点，则将左子用作前驱线索，并指向遍历的上一个节点
• 如果前一个节点没有右子节点，则将其右子用作后继线索，并指向当前节点

// TODO

使用线索二叉树来遍历

中序线索二叉树

中序线索二叉树的遍历过程为：

• 找前驱
  • 无左孩子：通过左线索找到
  • 有左孩子：左子树中的最右边一个节点（不一定是叶子）
• 找后继
  • 无右孩子：通过右线索找到
  • 有右孩子：右子树的最左边一个节点（不一定是叶子）

先序线索二叉树

找前驱：挺困难的

• 无左孩子：通过左线索找到
• 有左孩子：首先找到父节点
  • 如果当前节点是父节点的左子，那么前驱就是父节点
  • 如果当前节点是父节点的右子，那么前驱就是父节点左子树最右边的叶子

找后继：

• 无右孩子：通过右线索找到
• 有右孩子：后继就是左孩子，如果没有左孩子，后继就是右孩子

后序线索二叉树

找前驱：

• 无左孩子：通过左线索找到
• 有左孩子：前驱就是右孩子，如果没有右孩子，前驱就是左孩子

找后继：挺困难，相当于「先序线索二叉树找前驱」

• 无右孩子：通过右线索找到
• 有右孩子：先找到父节点
  • 如果当前节点是父节点的右子，那么后继就是父节点
  • 如果当前节点是父节点的左子，那么后继就是父节点右子树最左边的叶子

由于「后序线索二叉树」找后继是一件苦难的事情，所以「后序线索二叉树」的正序遍历还需要栈的支持。