最小生成树

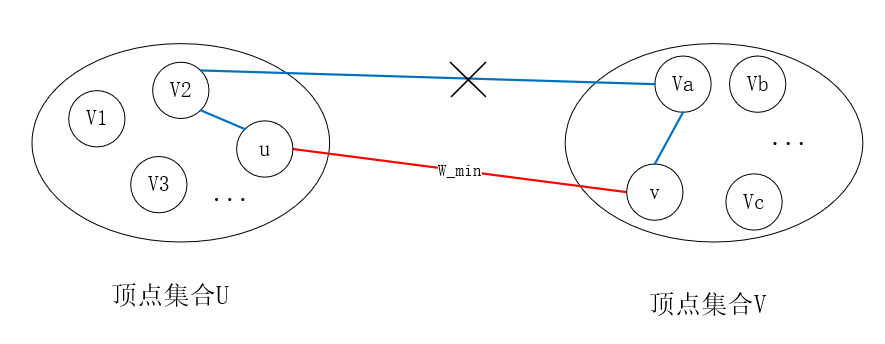
最小生成树：只有带权图才有最小生成树的概念，一般求解无向图的最小生成树。边权之和最小的生成树即为「最小生成树」。

注：生成树的树根并不影响生成树的唯一性，只要形状相同计算生成树是同一个。因此，所有边权重都不同的连通无向图其最小生成树唯一。

最小生成树的原理

最小生成树原理：将图的顶点集合分为两部分 ，分别从中取两个顶点 ，使得 是沟通两个顶点集合的权值最小的边，那么必定存在一棵最小生成树包含 边。

反证法证明： 如果不存在包含边 的最小生成树。任取一个最小生成树，向其中加入 边，得到一个环，删掉环中横跨 集合的另一条边，可以得到一棵新的生成树，这个生成树比原生成树更小。

Prim算法（贪婪的）

思想：从一个顶点开始，不断扩充当前顶点集合。初始时，将任意一个顶点添加进集合。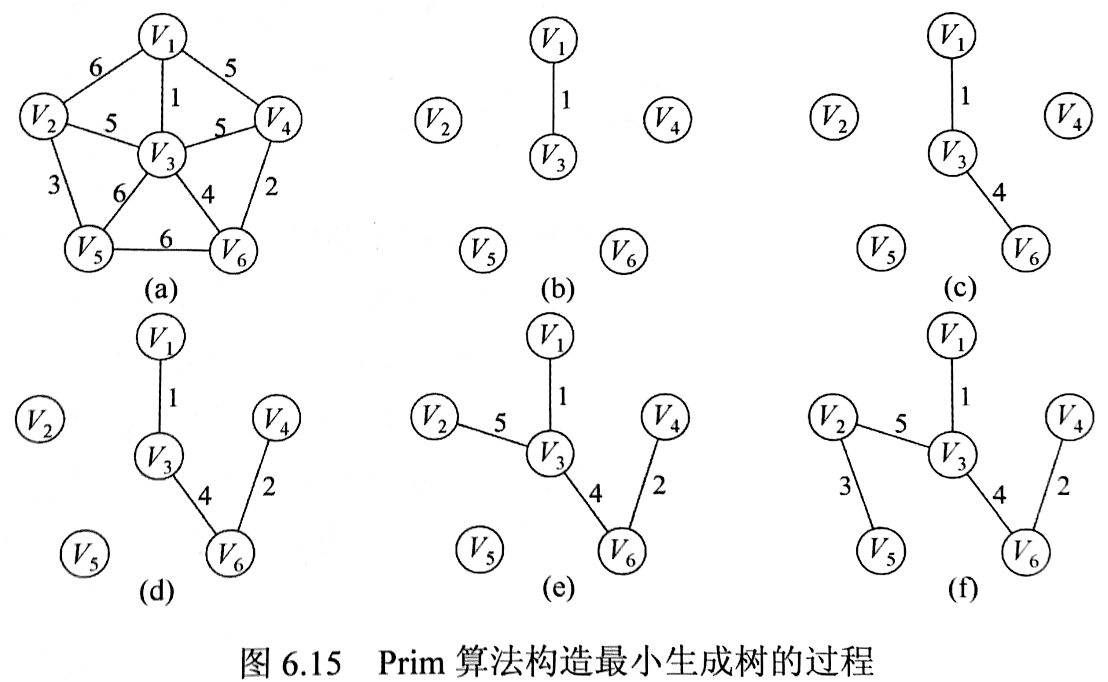

时间复杂度：，其中 为顶点个数
如何达到 ：维护一个数组 dis[n]，其中 dis[i] 表示「不在生成树中的顶点 」到生成树的最小距离。每次向生成树中添加一个顶点，就更新这个数组。

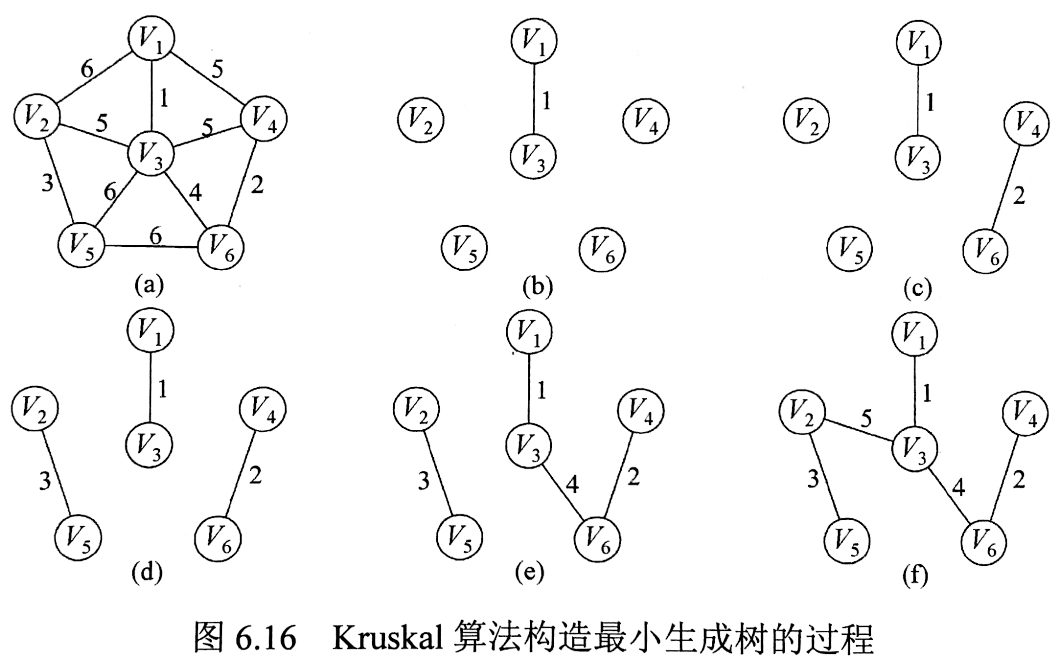
Kruskal算法（贪婪的）

思想：不断选择权值最小的边，将森林合并为一颗树。
辅助数据结构：

• 堆：用于选择权值最小的边
• 并查集：用于合并森林

时间复杂度：