树-森林

树的表示方法

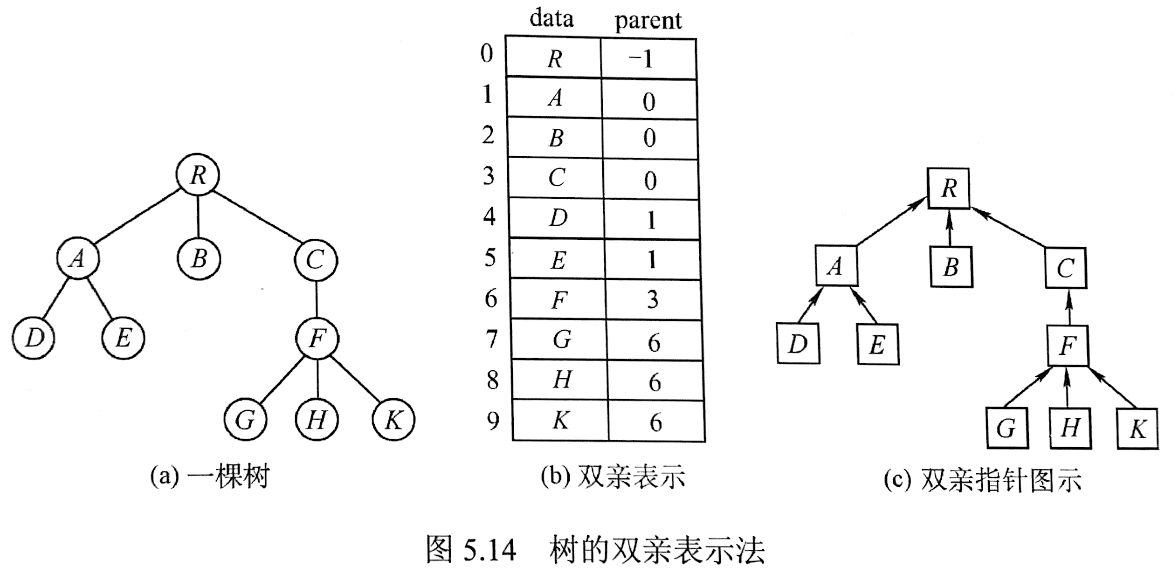
双亲表示法

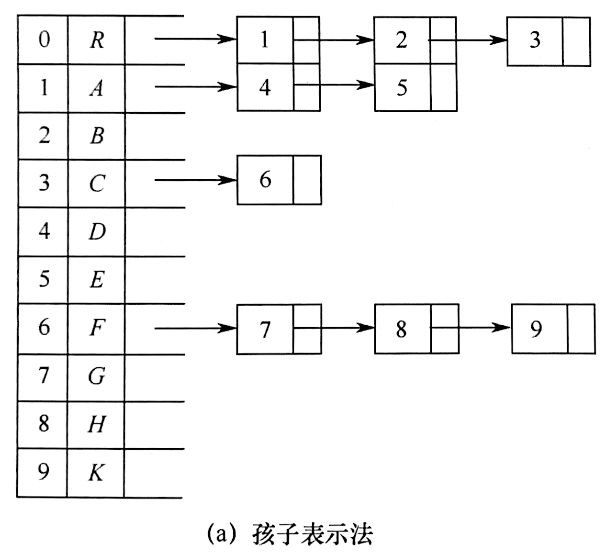
孩子表示法

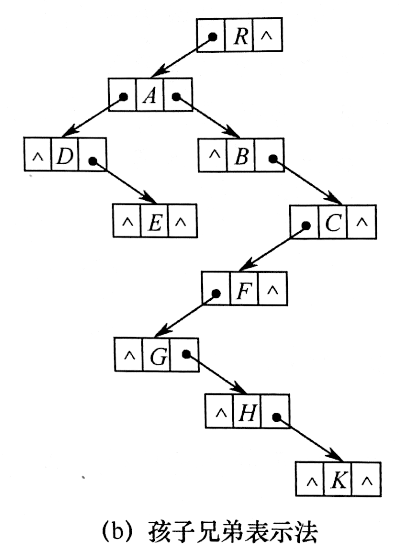
孩子兄弟表示法

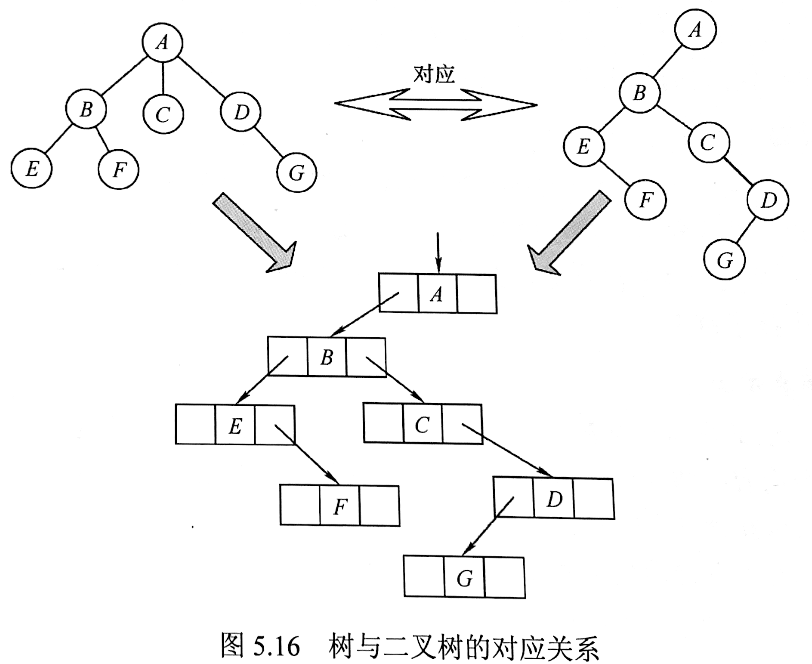
树/森林转换为二叉树

转换后的二叉树的左右指针的数量关系：

• 左指针指向的是树/森林的子节点。「二叉树左指针为空的节点数量」等于「树/森林中叶子节点的数量」
• 右指针指向的是兄弟节点。「二叉树右指针为空的节点数量」等于「树/森林中非叶子节点的数量」加1。（因为：每一个非叶子节点都有子节点，只有其最后一个子节点会贡献一个空的右指针，树的根节点或森林的最右树的根节点也会贡献一个空的右指针）

二叉树 <—> 树

二叉树 <—> 森林

森林转换为二叉树：

• 将每棵树都转换为二叉树
• 树之间是兄弟关系

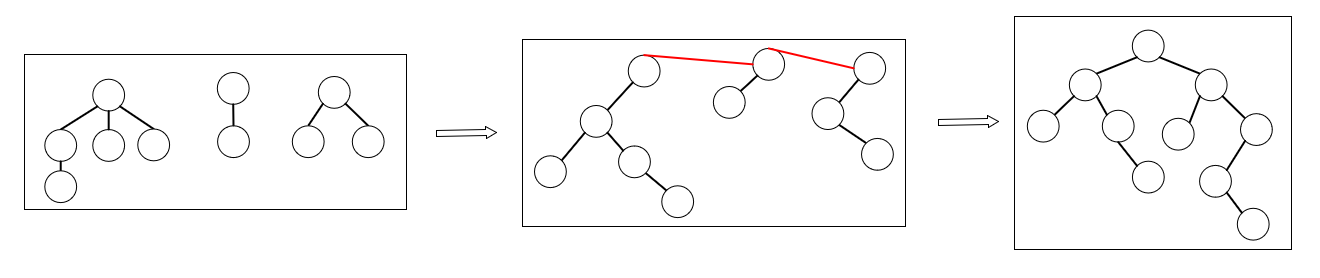
二叉树转换为森林：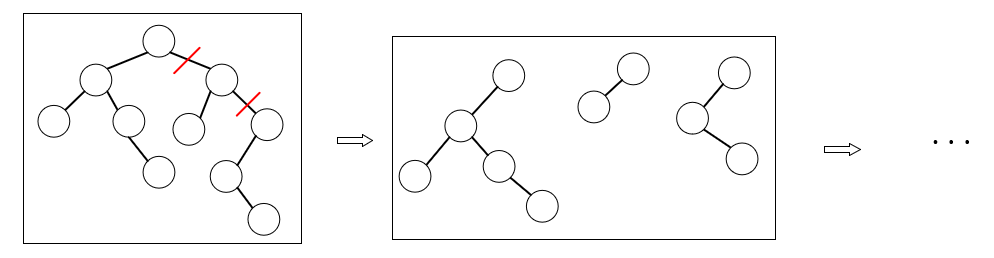

遍历

树的「先根遍历」相当于二叉树的「先序遍历」
树的「后根遍历」相当于二叉树的「中序遍历」

森林的「先序遍历」相当于二叉树的「先序遍历」
森林的「中序遍历」相当于二叉树的「中序遍历」

树的遍历

先根遍历：先访问根节点，再访问子节点
后根遍历：先访问子节点，再访问根节点

森林的遍历

「先序遍历」森林：

• 访问森林中第一棵树的根节点
• 对于第一棵树的子树森林，使用「先序遍历」
• 对于除第一棵树之外的其他树构成的森林，使用「先序遍历」

「中序遍历」森林：（相当于先子节点，再父节点）

• 对于第一棵树的子树森林，使用「中序遍历」
• 访问第一棵树的根节点
• 对于除了第一棵树之外的其他树构成的森林，使用「中序遍历」

注：为什么这里叫做中序遍历？因为访问根节点的操作被夹在中间，其前后都是递归遍历森林的操作

并查集

将森林中的多棵树合并为一棵树，使用树的双亲表示法比较方便