🔍二分查找

算法和程序设计技术的先驱Donald Ervin Knuth曾说：虽然二分查找的基本思想相对简单，但细节可能会非常棘手

这里提出一个二分查找的通用方法：

  • 离开循环的条件是：**l == r**。
  • 无匹配项时，返回左侧还是右侧，要看：
    • 左侧：mid = (l + r + 1) >> 1
    • 右侧：mid = (l + r) >> 1
  • 有匹配项时，返回左侧还是右侧，要看：
    • 左侧：r = mid
    • 右侧：l = mid
  • 但是，这里并没有四种组合，只有两种组合，另外两种会陷入死循环。最终得到的结果如下：

1. 无匹配项时，返回右侧；有匹配项时，返回左侧

  1. int find(vector<int>& a, int t) {
  2.     int l = 0;
  3.     int r = a.size() - 1;
  4.     while (l < r) {
  5.         int mid = (l + r) >> 1;
  6.         if (a[mid] < t)
  7.             l = mid + 1;
  8.         else // a[mid] >= t
  9.             r = mid;
  10.     }
  11.     return l;
  12. }

2. 无匹配项时，返回左侧；有匹配项时，返回右侧

  1. int find(vector<int>& a, int t) {
  2.     int l = 0;
  3.     int r = a.size() - 1;
  4.     while (l < r) {
  5.         int mid = (l + r + 1) >> 1;
  6.         if (a[mid] <= t)
  7.             l = mid;
  8.         else // a[mid] > t
  9.             r = mid - 1;
  10.     }
  11.     return l;
  12. }

思考路线：：选择i=mid还是j=mid？前者表示匹配时得到右端；然后，为了不陷入死循环，只能选择mid=(i + j + 1) >> 1（或者mid = (i + j) >> 1）。

🌴两个数组的中位数问题

题目描述

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。 请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。 你可以假设 nums1 和 nums2 不会同时为空。 示例 1:

  1. nums1 = [1, 3]
  2. nums2 = [2]
  3. 则中位数是 2.0

示例 2:

nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5

解题

问题的关键是时间复杂度要求为O(log(m+n))。
考虑将两个数组合并的情况：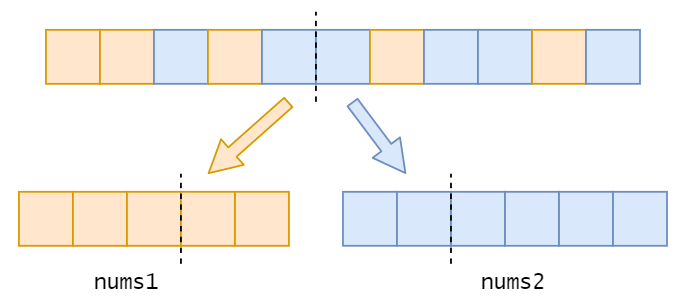
二分查找 - 图1
所以，只要找到合适的划分，确保nums1左侧元素个数和nums2左侧元素个数的和为(m+n)/2即可（在此只考虑m+n为奇数的情况）
合适的划分是指：LMax1 <= RMin2 && LMax2 <= RMin1。
此处有一个技巧：不考虑元素，而是考虑划分。例如：nums1有（m+1）种划分。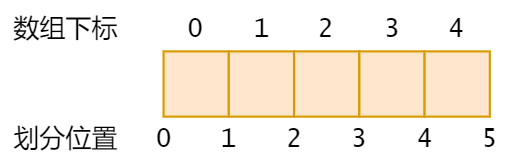
二分查找 - 图2
代码如下：复杂度可以达到：O(log(min(m, n)))，

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int m = nums1.size();
    int n = nums2.size();
    // 让 nums1 表示短的数组
    if (m > n)
        return findMedianSortedArrays(nums2, nums1);
    // 排除 m == 0 的情况
    if (m == 0)
        return (nums2[(n - 1) >> 1] + nums2[n >> 1]) * 1.0f / 2.0f;
    int al = 0;        // nums1数组划分位置的左限
    int ar = m;        // nums1数组划分位置的右限
    int LMax1, RMin1, LMax2, RMin2;
    while (al <= ar) {
        int i = (al + ar) >> 1;
        int j = ((m + n) >> 1) - i;
        LMax1 = i == 0 ? INT32_MIN : nums1[i - 1];
        RMin1 = i == m ? INT32_MAX : nums1[i];
        LMax2 = j == 0 ? INT32_MIN : nums2[j - 1];
        RMin2 = j == n ? INT32_MAX : nums2[j];
        if (LMax1 > RMin2)
            ar = i - 1;
        else if (LMax2 > RMin1)
            al = i + 1;
        else
            break;
    }
    if ((m + n) % 2 == 1)    // m + n 是奇数的情况
        return min(RMin1, RMin2);
    else                    // m + n 是偶数的情况
        return (max(LMax1, LMax2) + min(RMin1, RMin2)) * 1.0f / 2.0f;
}