辗转相除和更相减损的原理是一致的：两个数之间有最大公约数
gcd(a, b)，那么两数之差一定是最大公约数的整数倍；两数相除的余数也是最大公约数的整数倍。
辗转相除法/欧几里得算法
辗转相除，直到余数为零，最后的余数即为最大公约数。
以 72和 46为例：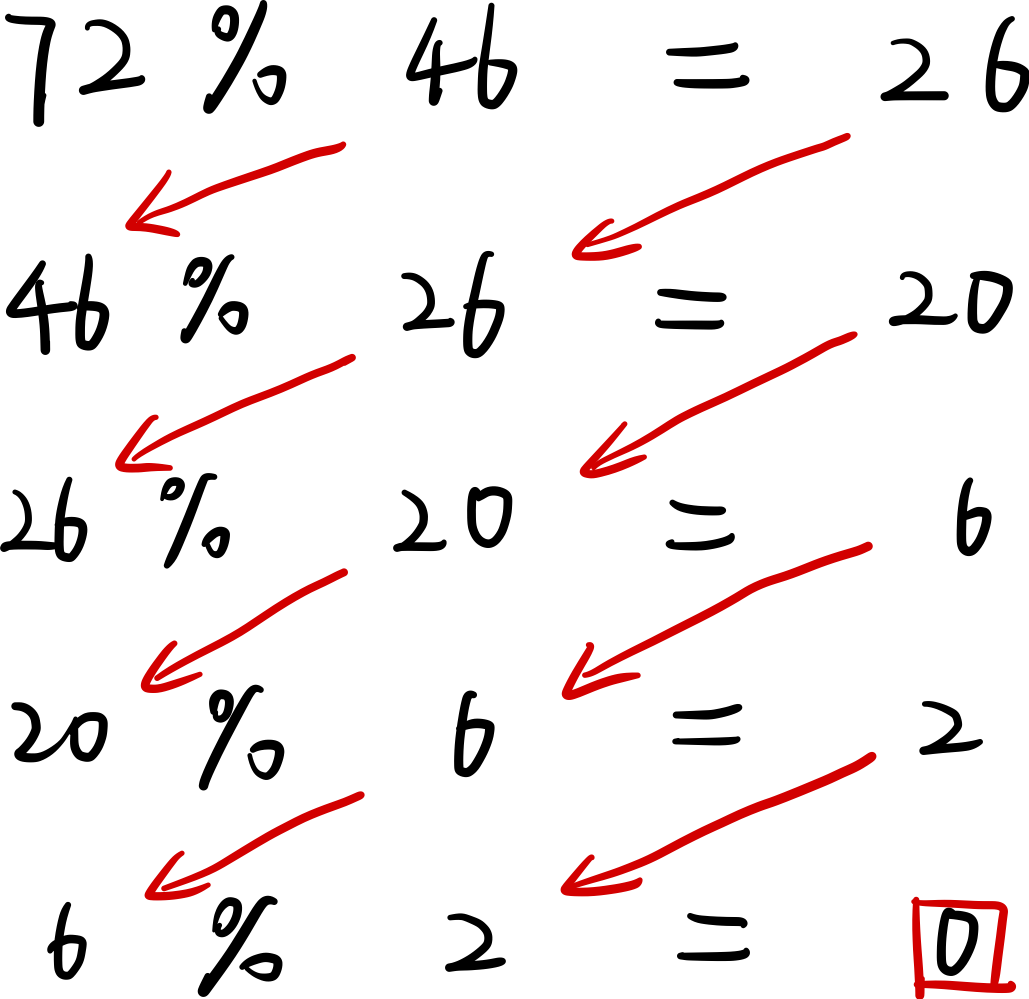
最后的最大公约数是 2
更相减损法
辗转相减，确保大数减小数，直到差为零，最后的减数就是最大公约数。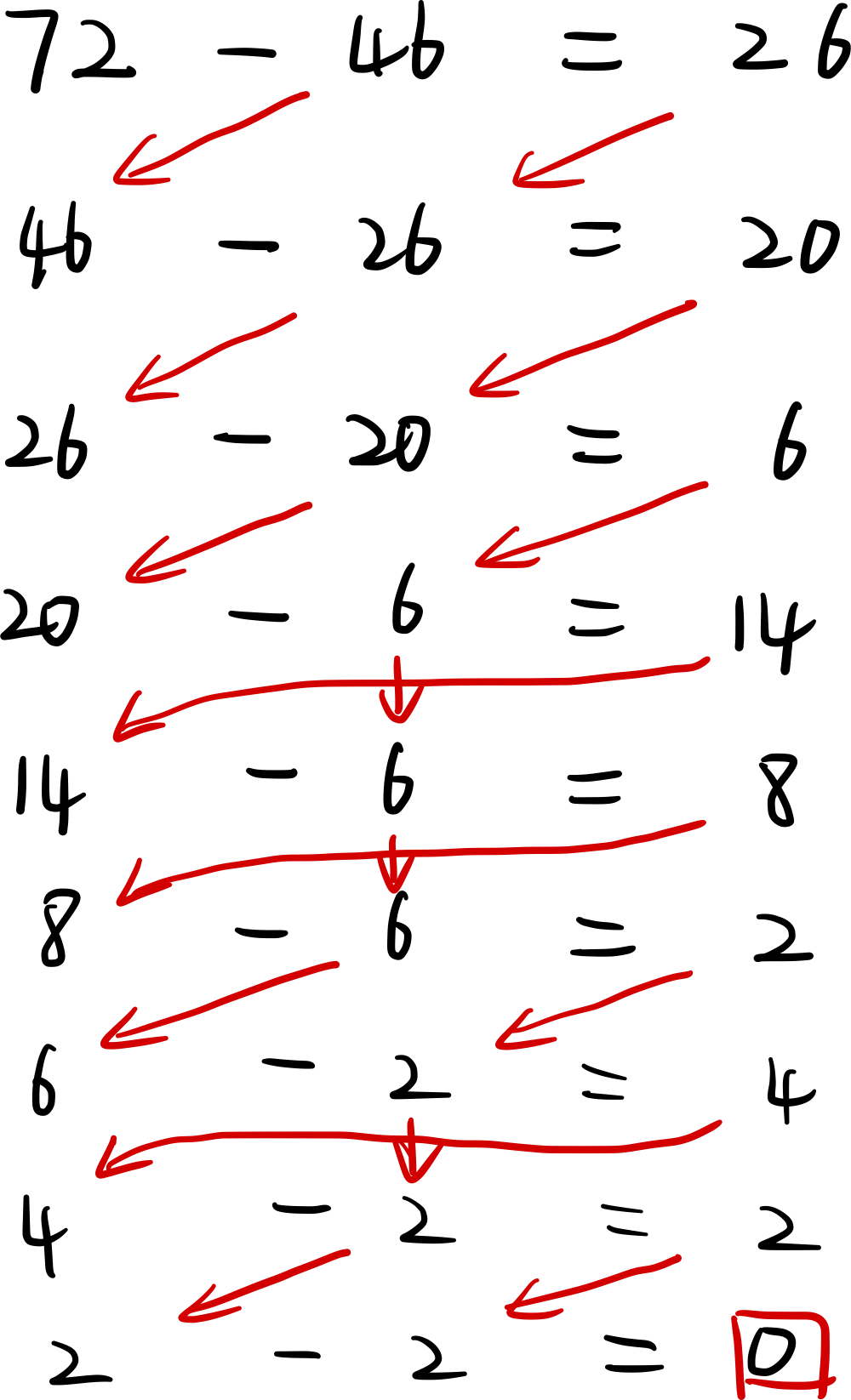
最后的最大公约数是 2
最小公倍数
最大公约数记为 gcd，最小公倍数记为 lcm，则有：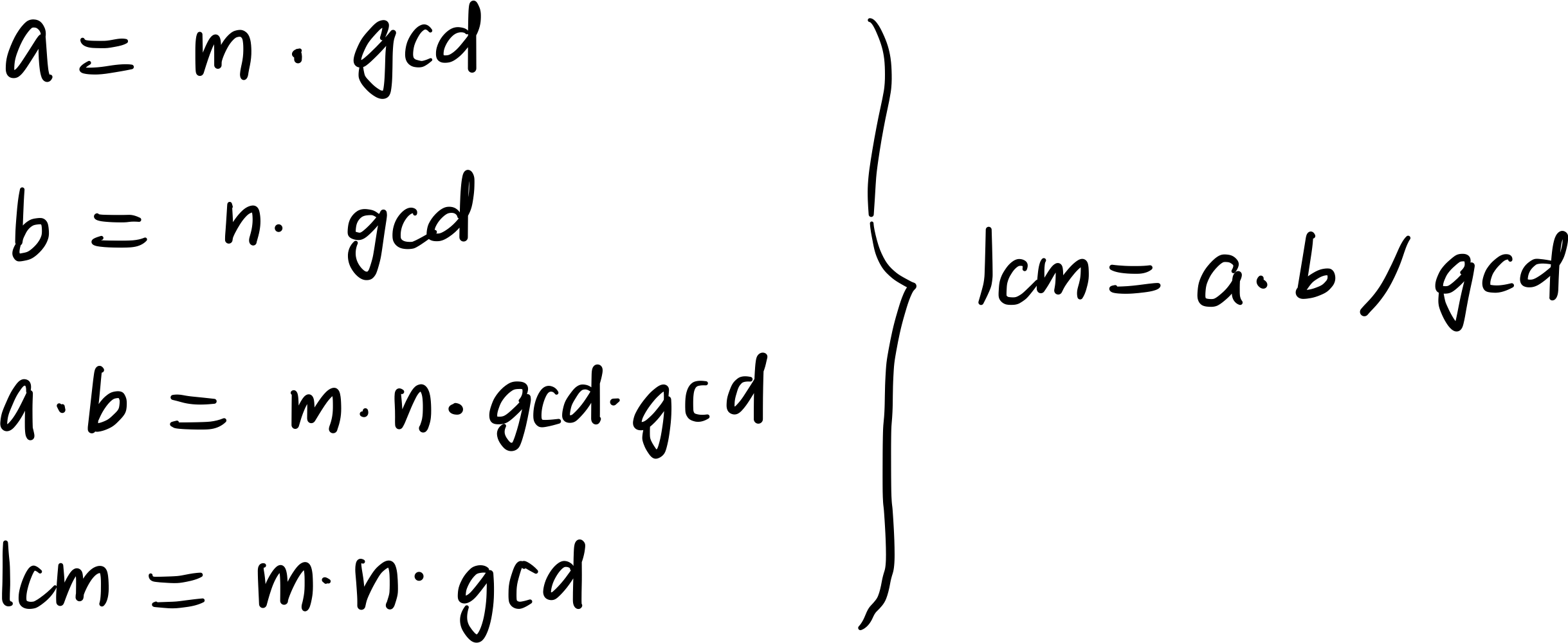
只要算出了最大公约数，很容易就能得到最小公倍数
若有收获，就点个赞吧
0 人点赞
