二叉查找树BST

二叉查找树BST

二叉查找树的插入

新插入的节点一定是叶节点

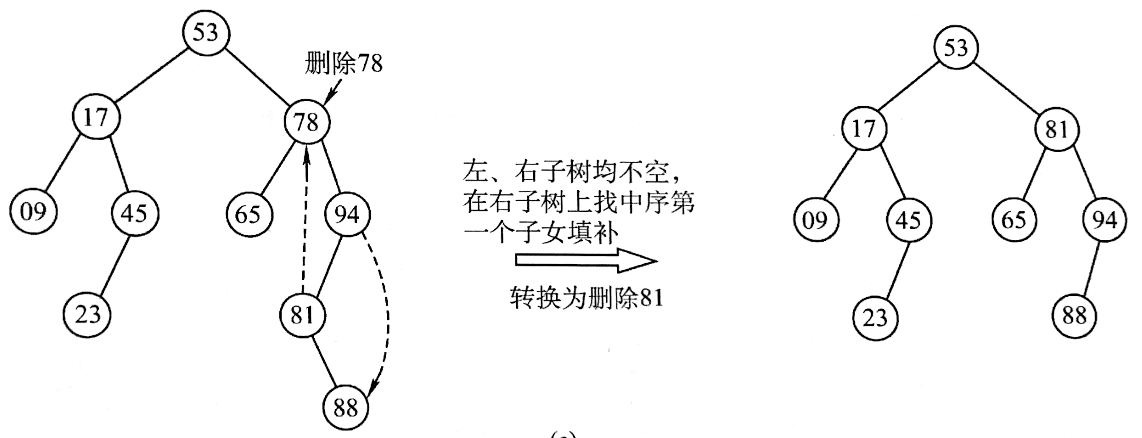
二叉查找树的删除

分 3 种情况讨论：

1. 如果删除的节点是叶子节点，则直接删除
2. 如果删除的节点只有左子树或者右子树，则替代
3. 如果删除的节点有左右子树，那么在左子树中寻找直接前驱，或者在右子树中寻找直接后继，将其摘除，替代当前节点即可。（删除直接前驱或者直接后继的过程中，一定是前两种情况）。

平衡二叉树 AVL

任意左右子树高度差不超过 1
平衡因子：左子树与右子树的高度差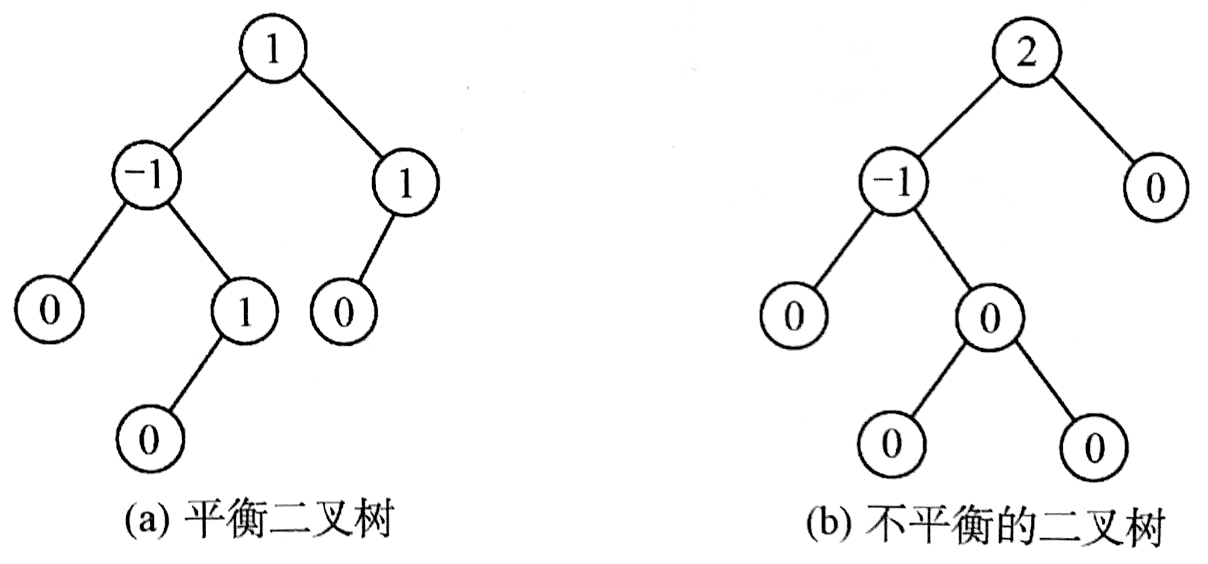

平衡二叉树的最大高度：

• 高度为 0 的平衡二叉树有 0 个节点
• 高度为 1 的平衡二叉树有 1 个节点
• 如果高度为 的平衡二叉树至少有 个节点，那么有：，满足贪心原则

高度为 的平衡二叉树最小节点数 为：

• 斐波那契数列的递推公式为：，通项为：

• 节点数通项可以写作：

• 斐波那契的首项：；最小节点数的首项为：

• 最终：节点数通项为：

平衡二叉树的插入

如何恢复平衡：因为插入导致二叉树不再平衡时，只需要找到第一个平衡因子绝对值大于 1 的节点，对其进行调整，即可让二叉树恢复平衡。

失衡情况可以归结为以下几种：（下面的模型可以覆盖任何的失衡情况）
LL（或对称的RR）：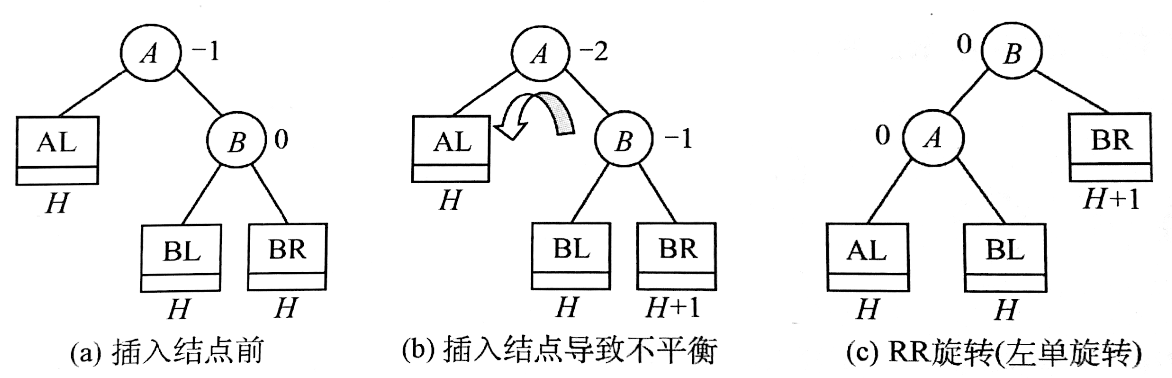

LR（或对称的RL）：
（其中 CL 和 CR 的高度可以互换）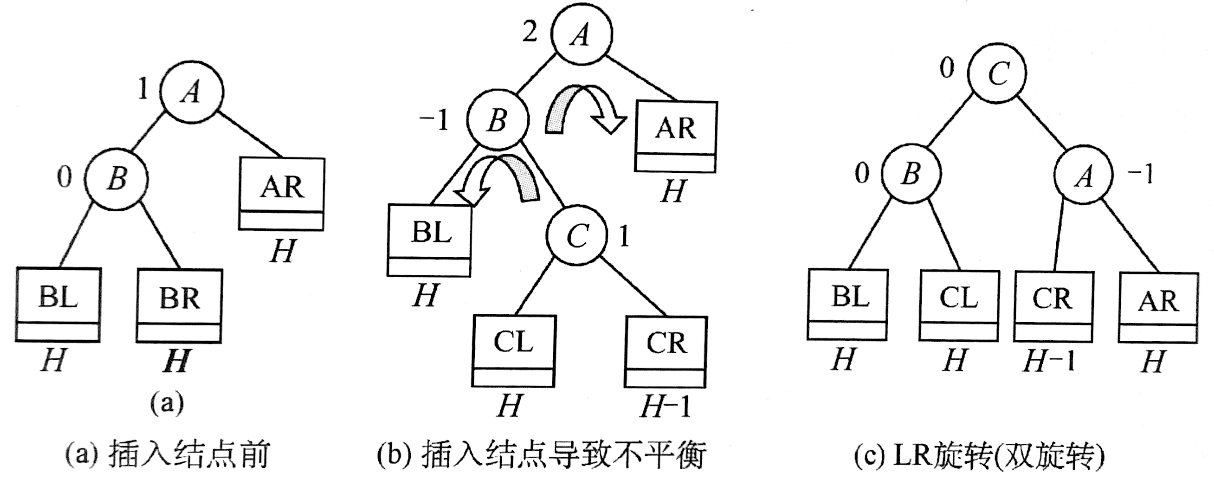

注：以上的旋转操作均不会改变「二叉查找树」的性质。