调用语法
G2 默认提供了如下 8 种几何标记和数据调整组合,直接通过如下代码即可调用:
chart.intervalStack().position('x*y');
| 类型 | 描述 |
|---|---|
pointStack |
层叠点图 |
pointJitter |
扰动点图 |
pointDodge |
分组点图 |
intervalStack |
层叠柱状图 |
intervalDodge |
分组柱状图 |
intervalSymmetric |
对称柱状图 |
areaStack |
层叠区域图 |
schemaDodge |
分组箱型图 |
另外也可以通过如下方式整合几何标记和数据调整方式来自由创建和组合图表,支持多种数据调整方式的组合。
chart.area().position('x*y').adjust({type: [ 'stack', 'symmetric' ]});
为什么进行数据调整
数据映射到图形时必须进行视觉编码,视觉编码包括几何标记和视觉通道,几何标记对应着多种图表类型,视觉通道定义图形属性。视觉通道中最具区分度的通道是位置(position),图形的位置在一些情况下会出现重叠:
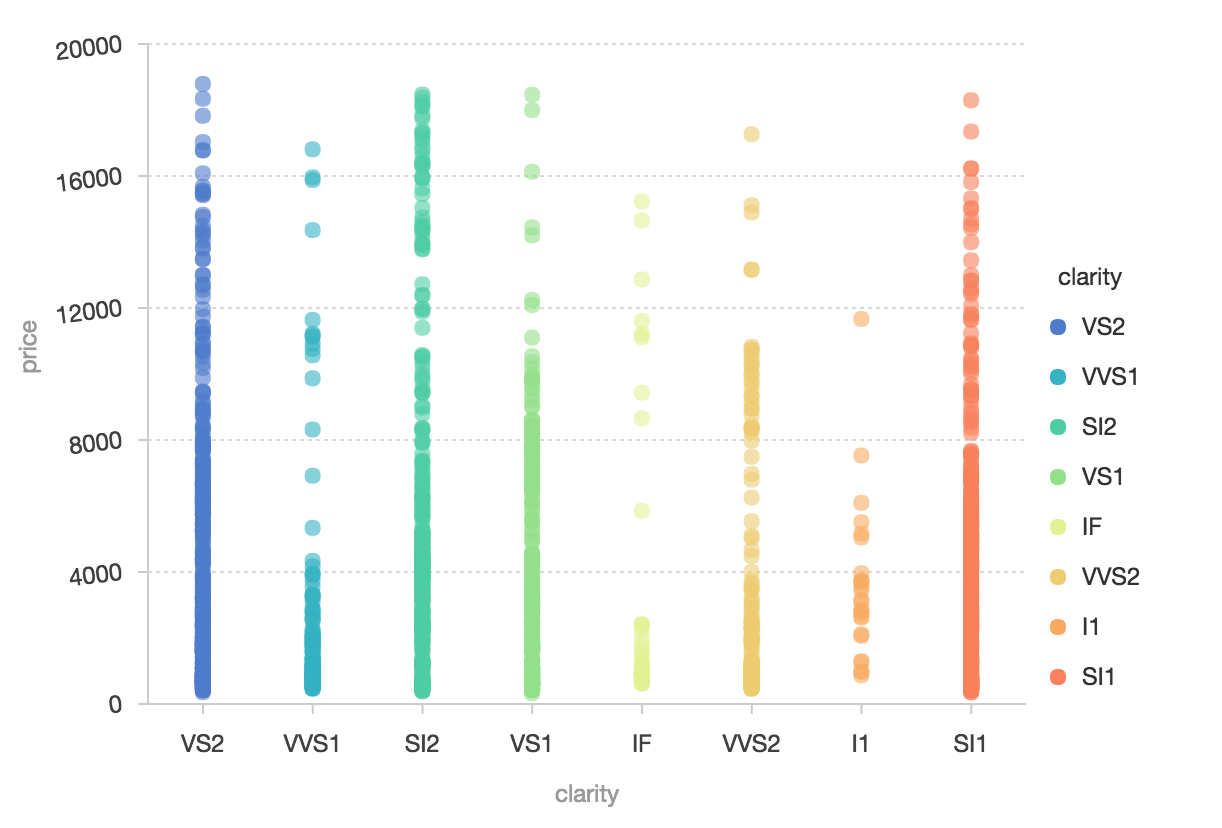
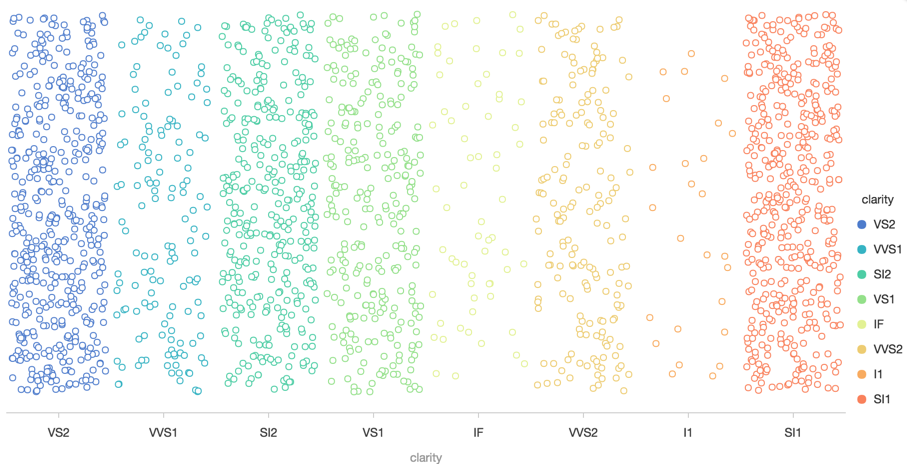
点图经常存在点重叠的情况。上图的点图有 2000 多条记录,大多数点重叠在一起;
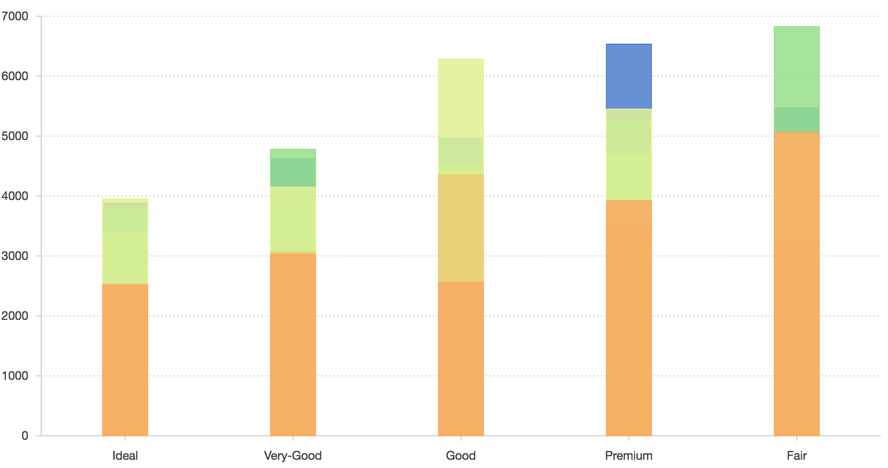
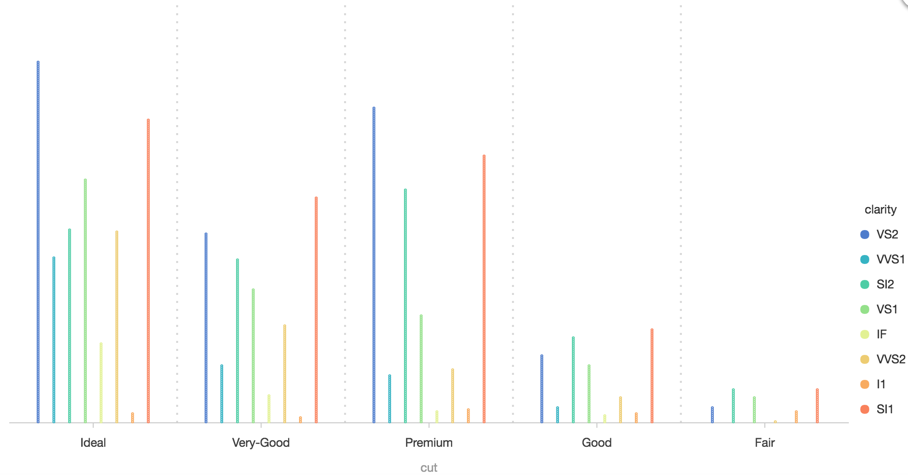
柱状图(interval) 在 x 轴是分类的情况下,同一个分类下有多条记录是也会重叠。上图的柱状图,每个分类下有 7 个柱状图,互相重叠,看不清晰各个分类的数据大小。
所以我们需要对数据进行调整,使得图形在画布上不互相重叠。G2 中支持以下几种数据调整:
| 名称 | 描述 |
|---|---|
| stack | 层叠,将同一个分类的数据值累加起来。以层叠柱状图为例,x 轴方向的同一个分类下面的数据,按照顺序,将 y 轴对应的值累加,最终将数据调整的不再重叠。 |
| jitter | 扰动散开,将数据的位置轻微的调整,使得映射后的图形位置不再重叠。 |
| dodge | 分组散开,将同一个分类的数据进行分组在一个范围内均匀分布,并排放置。 |
| symmetric | 对称处理,使得生成的图形居中对齐。 |
数据调整类型
下面我们从下面这两个方面对各个数据调整类型进行详解:
适合的数据类型
适合的几何标记
stack
适合的数据类型
层叠数据,适用于分类数据和连续数据,只要 x 轴方向的值相同,就会对 y 轴方向的值进行层叠处理,例如对于该条数据 [{a: 1,b: 10},{a:1, b: 12}],将字段 a 映射至 x 轴,b 映射到 y 轴方向,y 发生层叠处理后:
data = [{a: 1, b:[0,10]}, {a: 1, b: [10, 22]};
生成的图形:
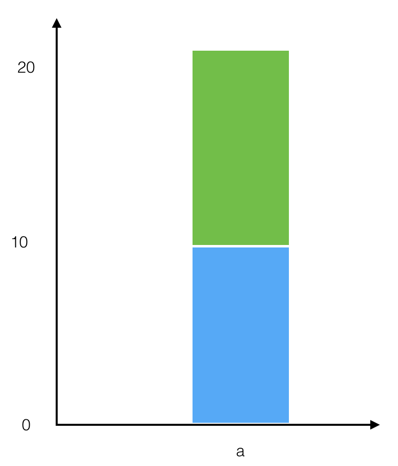
适合的几何标记
point、interval, area
- 层叠的点图
- 层叠的柱状图、玫瑰图
- 饼图,饼图本质上就是数据层叠占满了整个0-360度的圆形空间
jitter
适合的数据类型
jitter,仅适合于分类数据,只能在同一个分类的范围内散开,这不会改变图形表现的分类值。但是连续数据不能进行散开,连续数据位置一旦变化,图形代表的数据值就会不准确,会带来误导。
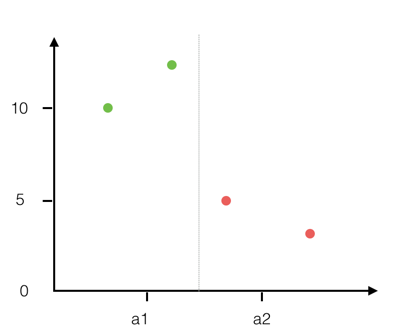
对数据进行 jitter 调整时,需要将分类数据转换成索引值,在索引值 [-0.5, 0.5] 的范围内进行随机分布,jitter 示例:
数据:
const data = [{ a: 'a1', b: 10 },{ a:'a1', b: 12 },{ a: 'a2', b: 5 },{ a:'a2', b: 3 }];
分类转换成数字:
const data = [{ a: 0, b: 10 },{ a: 0, b: 12 },{ a: 1, b: 5 },{ a: 1, b: 3 }];
随机散开数据
const data = [{ a: -0.3, b: 10 },{ a: 0.2, b: 12 },{ a: 0.8, b: 5 },{ a: 1.4, b: 4 }];
生成的图形:
适合的几何标记
point
- 散开的点图:
dodge
适合的数据类型
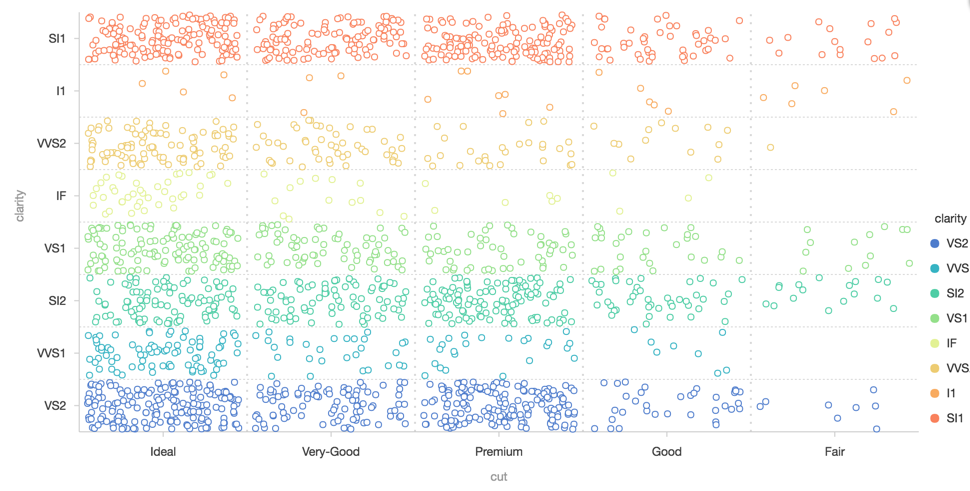
dodge 是将同一个分类的数据均匀得分布在分类的范围内,形成分组效果,同样不适合连续数据。dodge 跟 jitter 的差别在于:
dodge 的数据在分类范围内将数据均匀分布;
如果数据只有一维,y 轴方向无数据,那么 jitter 在整个 y 轴方向随机分布,而 dodge 在 y 轴方向层叠分布。
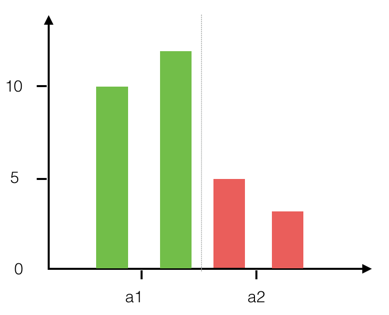
数据:
const data = [{ a: 'a1', b: 10 },{ a: 'a1', b: 12 },{ a: 'a2', b: 5 },{ a: 'a2', b: 3 }];
分类转换成数字:
const data = [{ a: 0, b: 10 },{ a: 0, b: 12 },{ a: 1, b: 5 },{ a: 1, b: 3 }];
均匀分布
const data = [{ a: -0.25, b: 10 },{ a: 0.25, b: 12 },{ a: 0.75, b:5 },{ a: 1.25, b:4 }];
生成的图形:
适合的几何标记
point interval schema
- 一维点图
- 二维的柱状图、玫瑰图(interval)
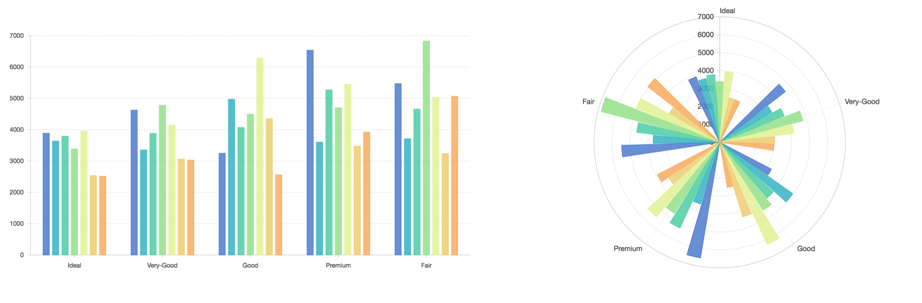
symmetric
适合的数据类型
symmetric 将数据沿 y 轴进行对称处理,所以适合处理连续数据。由于对称处理将单个值的数据处理成了有上下限的数值,所以不会引起数据的误解。
数据:
const data = [{ a: 'a1', b: 10 },{ a: 'a2', b:5 },{ a:'a3', b:20 }];
对称处理数据,由于 b 的范围是 [0 - 20],所以所有的数据都将在 0-20 之间对称,计算公式如下:
offset = (max - min - value)/2;
调整结果:
[min + offset, value + offset]
data = [{ a: 'a1', b: [ 5, 15 ] },{ a: 'a2', b: [ 7.5, 12.5 ] },{ a:'a3', b: [ 0, 20 ] }];
生成的图形:
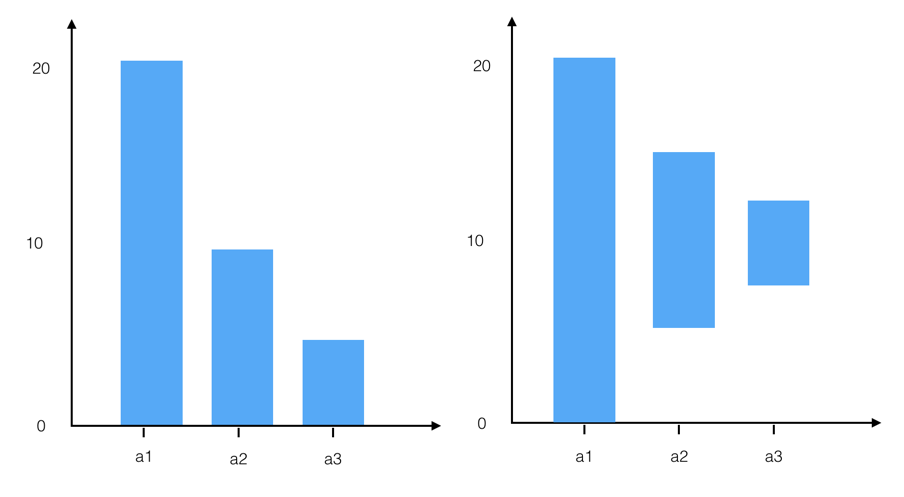
适合的几何标记
interval area
- 漏斗图:将柱状图调整成对称柱状图,然后再连接柱状图的顶点,即可成为漏斗图
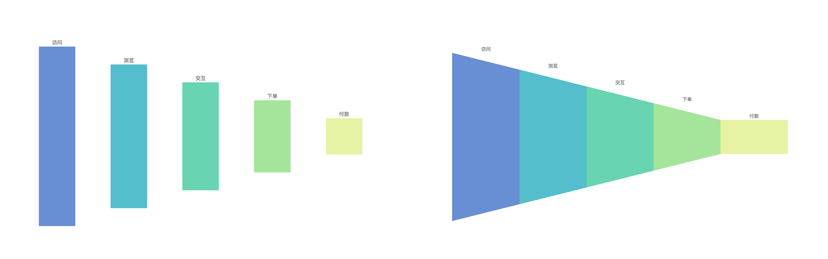
- 数据流图:对称的层叠区域图