计数排序思路

• 计数排序是一种稳定的时间复杂度算法，其时间复杂度为#card=math&code=O%28n%20%2B%20k%29&id=YfoUg)
• 计数排序本质上是鸽巢原理的应用，是空间换取时间的典型例子。计数排序不是基于比较的排序算法。
• 计数排序引入了一个统计数组，假定其为rec，那么rec[i]表示原始数组中数值等于i的元素个数。
• 例子：如果有10个人，其中有8个人身高比Alice矮，那么，Alice的身高就是第9矮的。
• 算法流程如下：
  1. 找出待排序数组中最大和最小的元素。
  2. 统计数组中每个数值为i的元素出现的个数rec[i]，存入数组的第i - min_value项。
  3. 对所有的计数进行累加，得到前缀和数组summ[i]（第0项是0)。
  4. 反向填充目标数组，将每个元素i放在目标数组target的第summ[i + 1] - 1位置，然后执行summ[i + 1] -= 1 。(怎么理解，对于元i而言，它前面有多少项？就是summ[i + 1] - 1项，因为summ[i + 1] = rec[0] + rec[1] + rec[2] + ... rec[i - 1] + rec[i]，长度是i + 1。所以，对于当前i而言，summ[i + 1]意味着的所有元素的个数，那么。前面有summ[i + 1] - 1个数，其下标自然就是summ[i + 1] - 1。
• 以[3, 1, 2, 1, 2, 5, 5, 5]为例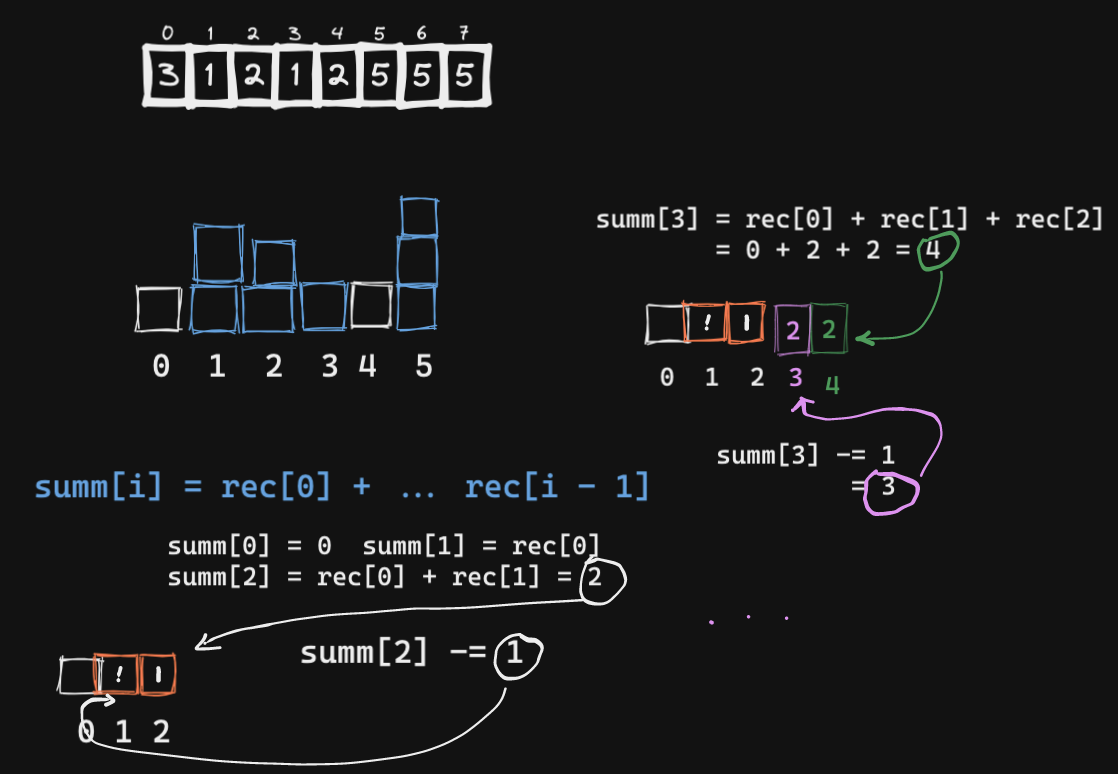
  

  计数排序代码

  ```cpp

  include

using namespace std;

void print_arr(vector& nums) { for (int i = 0, n = nums.size(); i < n; i++) { cout << nums[i] << “ “; } cout << endl; }

vector count_sort(vector& nums) { int min_num = min_element(nums.begin(), nums.end()); int max_num = max_element(nums.begin(), nums.end()) - min_num; int n = nums.size();

vector<int> rec(max_num + 5, 0);
vector<int> summ(max_num + 5, 0);
vector<int> ans(n, 0);
for (int i = 0; i < n; i++) {
    nums[i] -= min_num;
    rec[nums[i]] += 1;
}
for (int i = 1; i <= max_num + 1; i++) {
    summ[i] = summ[i - 1] + rec[i - 1];
}
for (int i = 0; i <= max_num; i++) {
    for (int j = 0; j < rec[i]; j++) {
        ans[summ[i + 1] - 1] = i + min_num;
        summ[i + 1] -= 1;
    }
}
return ans;

}

int main() { int n = 0; cout << “please input the size of array: “ << endl; cin >> n;

vector<int> nums(n, 0);
cout << "please input the array" << endl;

for (int i = 0; i < n; i++) {
    cin >> nums[i];
}

print_arr(nums);
nums = count_sort(nums);
print_arr(nums);

return 0;

} ```

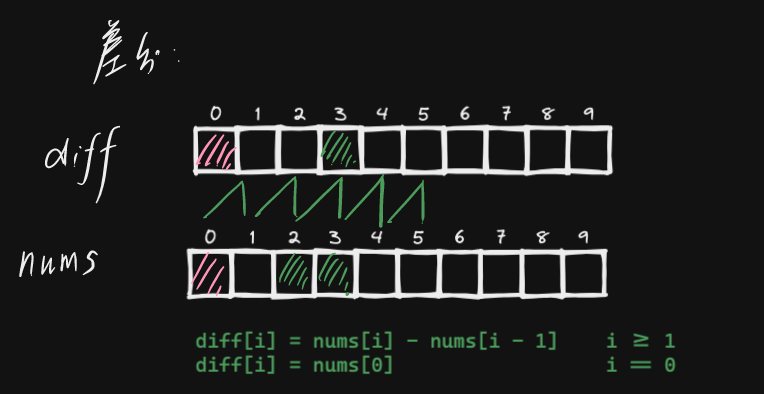
ps : 关于前缀和与数组，几个基本的图需要记住

• fig1: 前缀和
  
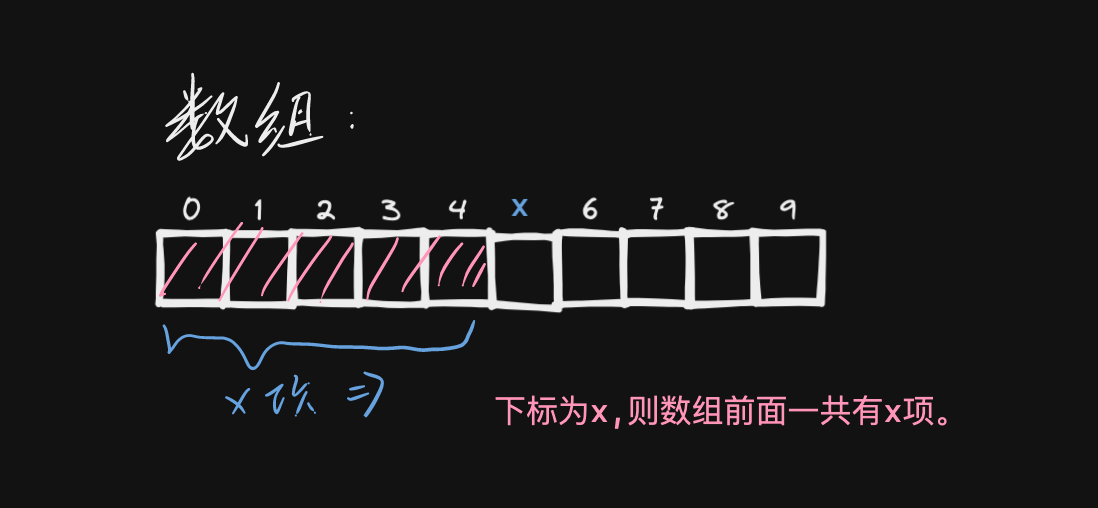
• fig2: 数组
  
• fig3: 差分