> https://leetcode-cn.com/problems/count-number-of-maximum-bitwise-or-subsets/solution/by-tong-zhu-mmeu/
思路1:不优化的回溯(穷举)
对于nums的每个位置而言,都有两种状态,就是“选”或者“不选”,那么假设有位,就应当有
种选择方案,如果方案符合条件,就将其放入子集方案中,否则不放入。
对于回溯的树来讲,就是一颗二叉树,每个非叶子节点有两个分支,分别代表“选择”和“不选择”,第i层的节点,就是nums[i],这样就可以通过dfs树来遍历。
脑子里面要有下面这张图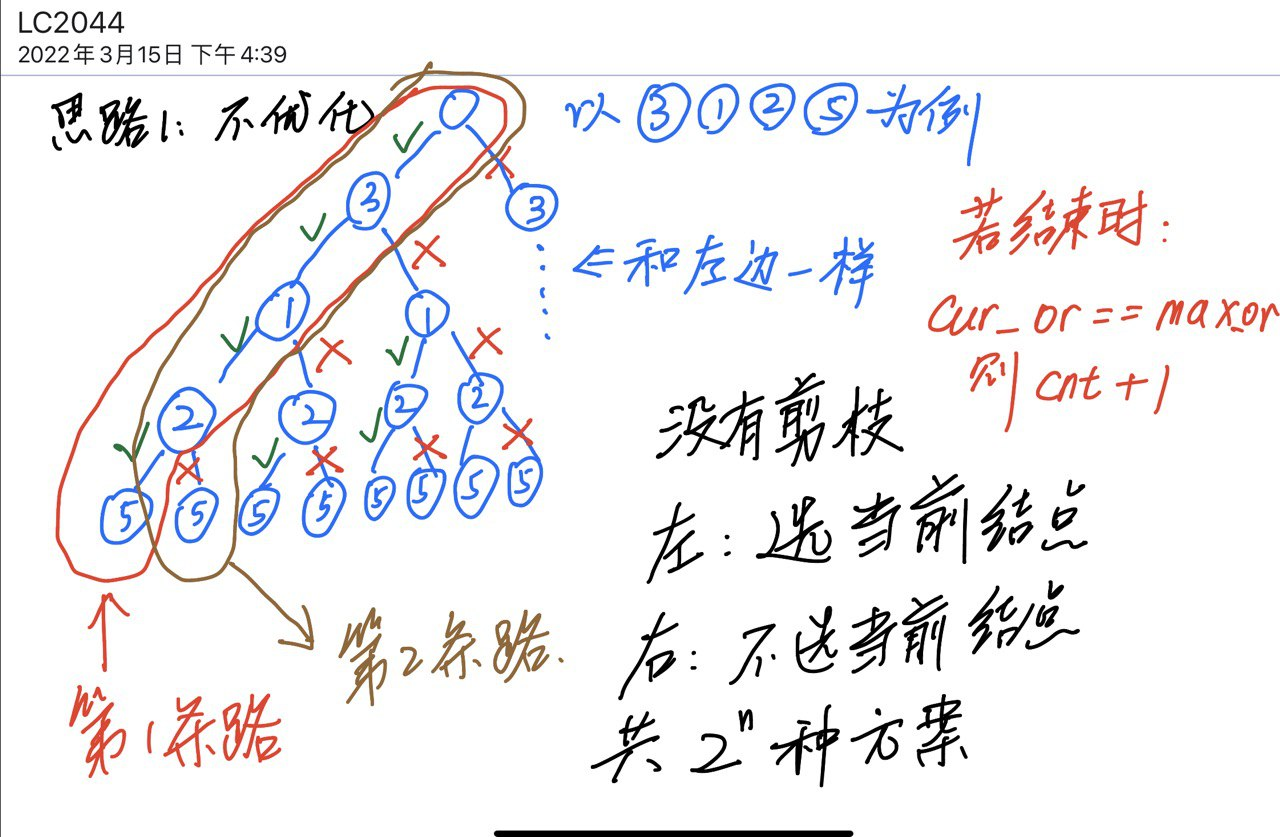
代码1:
class Solution {public:void dfs(int& count_subs, vector<int>& nums, int cur_depth, int num_size, int cur_or, int max_or) {if (cur_depth == num_size) {if (max_or == cur_or) {count_subs++;}return;}// 选择当前节点,也就是树的左分支dfs(count_subs, nums, cur_depth + 1, num_size, cur_or | nums[cur_depth], max_or);// 不选择当前节点,也就是树的右分支dfs(count_subs, nums, cur_depth + 1, num_size, cur_or , max_or);}int countMaxOrSubsets(vector<int>& nums) {int count_subs = 0;int max_or = 0;for (int num : nums) {max_or |= num;}dfs(count_subs, nums, 0, nums.size(), 0, max_or);return count_subs;}};
思路2:回溯穷举(带剪枝)
可以对树进行剪枝。优化两点:1.树本身的结构不一样 2.加入了剪枝<br /> 首先,可以**通过树的叶子节点一定是数组的最后一个元素**这样的办法,来简化树的形状。<br /> 然后,统计最大的按位或的结果,也就是所有元素全部或一遍。得到`max_or`。<br /> 接着,遍历简化之后的那棵树,如果当前的按位或结果`cur_or`和`max_or`相等,那么,就说明剩下的所有元素都是可有可无的。剩下的元素一共`num_size - cur_depth`个,那么,对应的`cur_depth`下,一共应该有个子集。否则,就继续DFS遍历这棵树。<br />“以数组的最后一个数字作为叶子节点”和“二叉是否选择当前节点”的两棵树之间的异同:<br />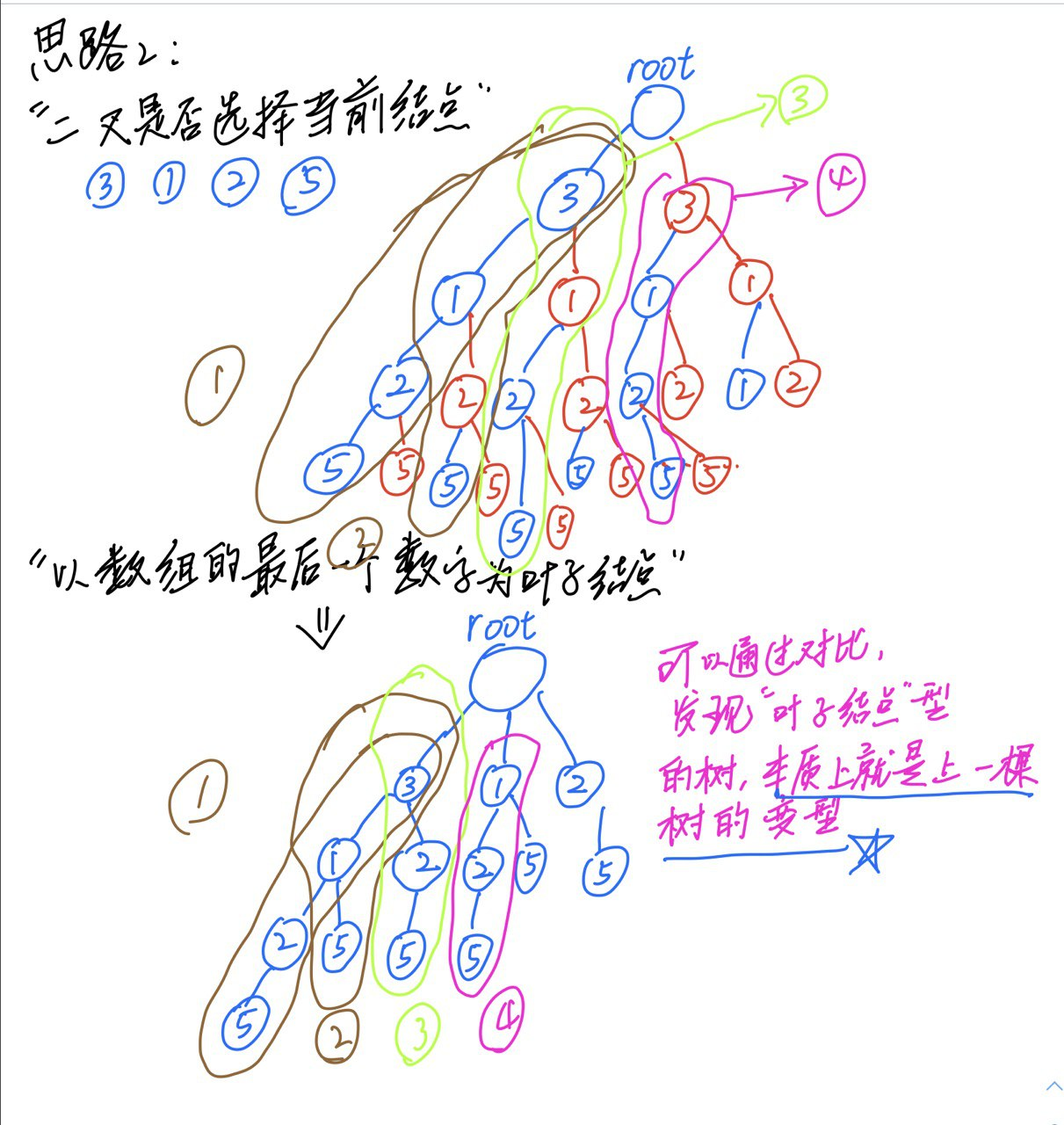<br />然后加上剪枝条件,提前返回就可以得到最优化的方案了。(两棵树本质上就是一棵树的两种呈现形式)
代码2:
class Solution {
public:
int count_subs = 0;
void dfs(vector<int>& nums, int cur_depth, int cur_or, int max_or) {
int num_size = nums.size();
if (cur_or == max_or) {
count_subs += (1 << (num_size - cur_depth));
return;
}
for (int i = cur_depth; i < num_size; ++i) {
dfs(nums, i + 1, cur_or | nums[i], max_or);
}
}
int countMaxOrSubsets(vector<int>& nums) {
int max_or = 0;
for (int num : nums) {
max_or |= num;
}
dfs(nums, 0, 0, max_or);
return count_subs;
}
};

