思路1：建立二叉树 + 回溯（左孩子选，右孩子不选）

  • 本质上是一颗二叉树，对于数组中的每个数字而言，可以被选择，也可以不被选择。走左边就是被选择，走右边就是不被选择。
  • 如何确保一个数字可以重复被选择，下一层遍历的时候，依然从当前下标index开始，而不是从index + 1开始，backtrace(ans, res, target - candidates[index], candidates, index)
  • 剪枝条件是什么？target == 0
  • 如何进行回溯？ res.pop_back()

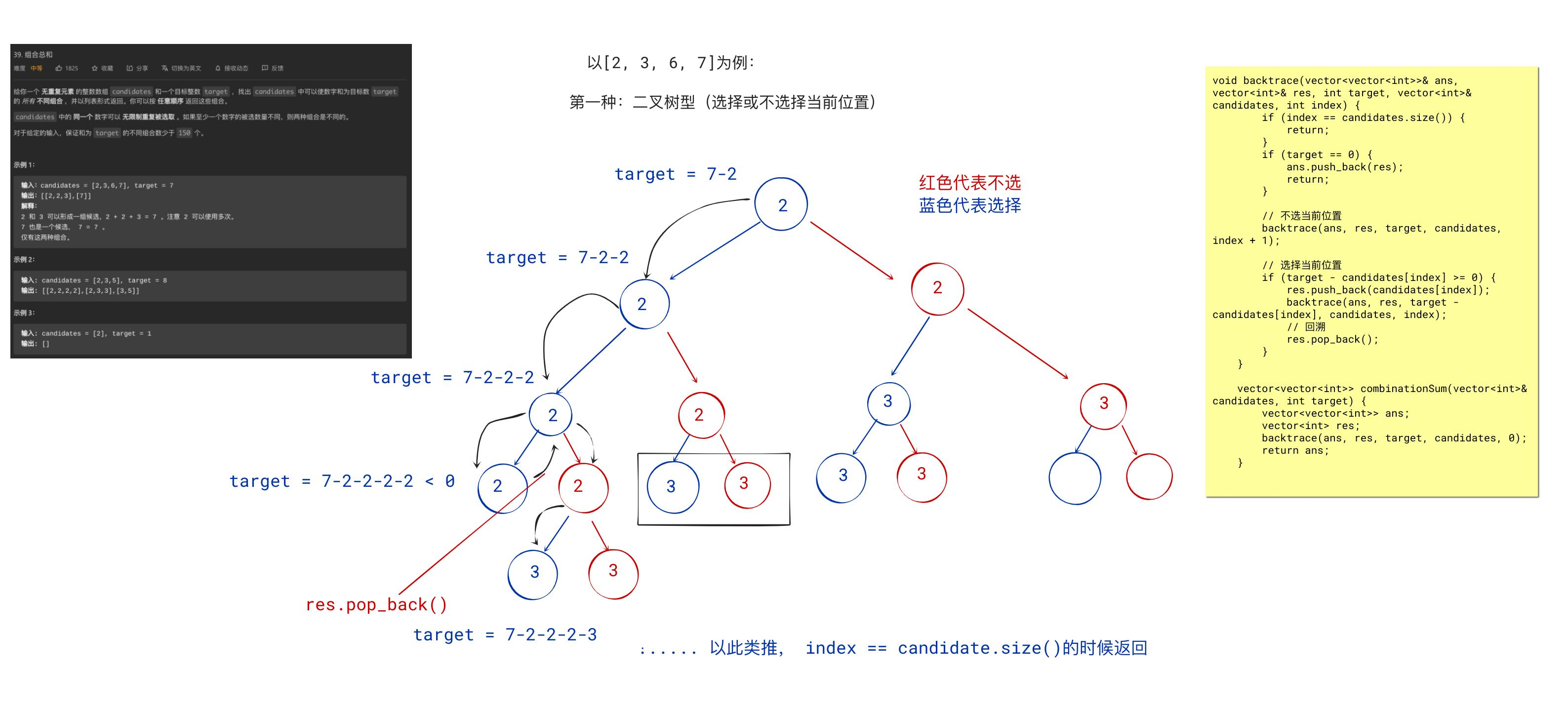
image.png

代码1：

  1.     void backtrace(vector<vector<int>>& ans, vector<int>& res, int target, vector<int>& candidates, int index) {
  2.         if (index == candidates.size()) {
  3.             return;
  4.         }
  5.         if (target == 0) {
  6.             ans.push_back(res);
  7.             return;
  8.         }
  10.         // 不选当前位置
  11.         backtrace(ans, res, target, candidates, index + 1);
  13.         // 选择当前位置
  14.         if (target - candidates[index] >= 0) {
  15.             res.push_back(candidates[index]);
  16.             backtrace(ans, res, target - candidates[index], candidates, index);
  17.             // 回溯
  18.             res.pop_back();
  19.         }
  20.     }
  22.     vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
  23.         vector<vector<int>> ans;
  24.         vector<int> res;
  25.         backtrace(ans, res, target, candidates, 0);
  26.         return ans;
  27.     }

思路2：叶子节点是数组最后一个元素

  • 和思路一本质上是一棵树，但是对形状进行优化
  • 剪枝条件不变
  • 通过遍历数组的方式建树，下一轮循环的开始不是cur_subscript + 1，而是cur_subscript（因为当前数字可以被用很多次）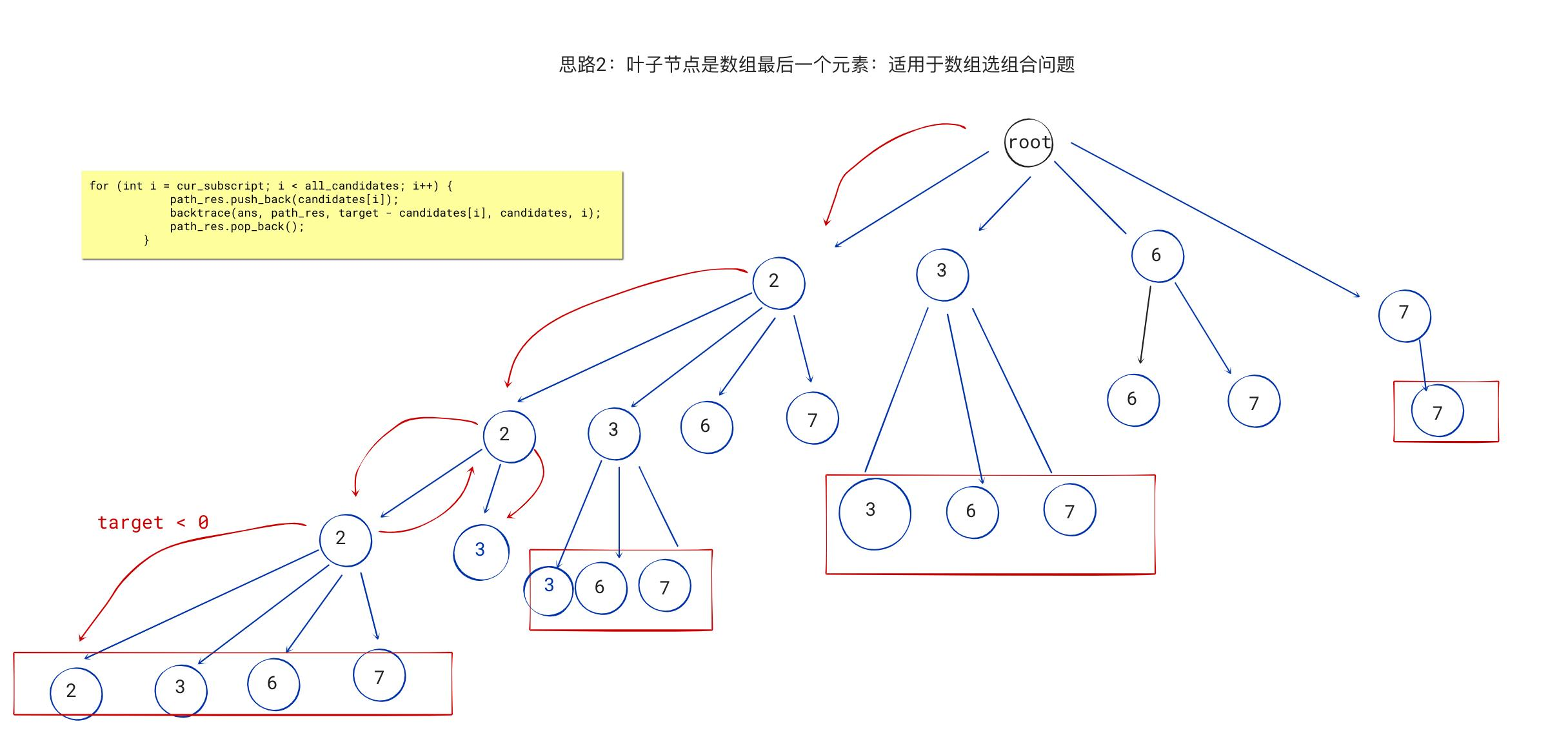
  • image.png

    代码2：

  1.     void backtrace(vector<vector<int>>& ans, vector<int>& path_res, int target, vector<int>& candidates, int cur_subscript) {
  2.         int all_candidates = candidates.size();
  3.         if (cur_subscript == all_candidates || target < 0) {
  4.             return;
  5.         }
  6.         if (target == 0) {
  7.             ans.push_back(path_res);
  8.             return;
  9.         }
  11.         // 按照数组来建立树
  12.         for (int i = cur_subscript; i < all_candidates; i++) {
  13.             path_res.push_back(candidates[i]);
  14.             backtrace(ans, path_res, target - candidates[i], candidates, i);
  15.             path_res.pop_back();
  16.         } 
  17.     }
  18.     vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
  19.         vector<vector<int>> ans;
  20.         vector<int> path_res;
  21.         backtrace(ans, path_res, target, candidates, 0);
  22.         return ans;
  23.     }