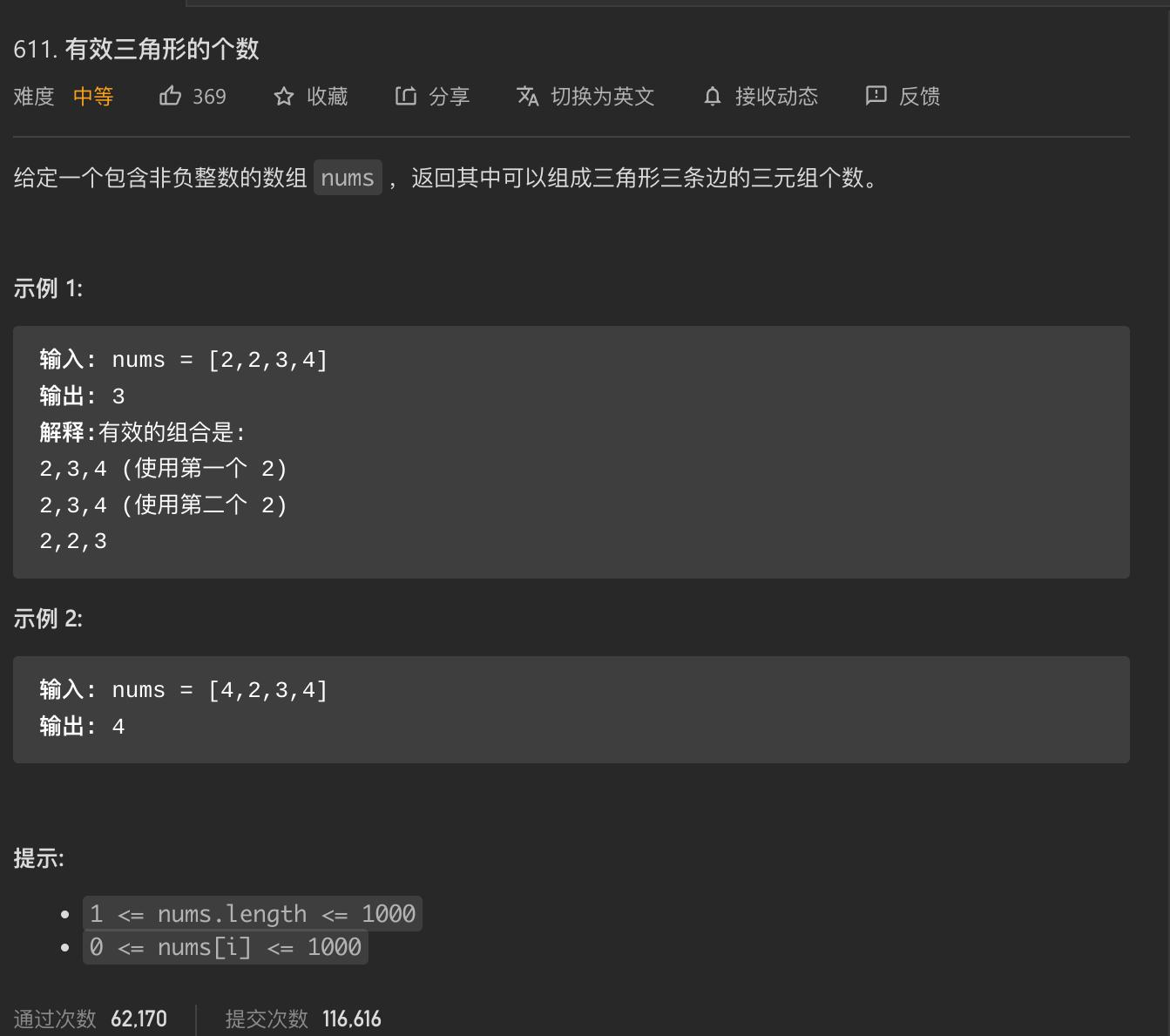
题目

思路

• 首先排序，通过有序性才能确定二分性
• 确定第一个边，最小的边，nums[i]，然后j = i + 1，选择第二条边nums[j],然后逐个遍历数组，这样就不会出现的重复的现象。
• 确定了前两条边之后，问题在于如何找第三条边，第三条边在[j, n - 1]区间当中，n为数组整体长度。可以通过二分找到符合小于两边之和条件的最后一条边，相当于符合条件区间的右端点，然后通过这个位置就可以得到第三条边的数量。

• 需要注意的是，如果不存在符合条件的区间，边缘的情况需要独立处理。二分往往会遇到这种问题。

  代码

  class Solution {
    public:
    int triangleNumber(vector<int>& nums) {
        int n = nums.size();
        if (n <= 2) {
            return 0;
        }
        sort(nums.begin(), nums.end());
        int cnt = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                int left = j + 1, right = n - 1;
                while (left < right) {
                    int mid = (left + right + 1) / 2;
                    // 取符合区间的右端点
                    if (nums[mid] < nums[i] + nums[j]) {
                        left = mid;
                    } else {
                        right = mid - 1;
                    }
                }
                cnt += (right - j);
                // 如果右端点恰好卡在左边界上
                if (right == j + 1) {
                    cnt -= (nums[right] >= nums[i] + nums[j] ? 1 : 0);
                }
            }
        }
        return cnt;
    }
  };