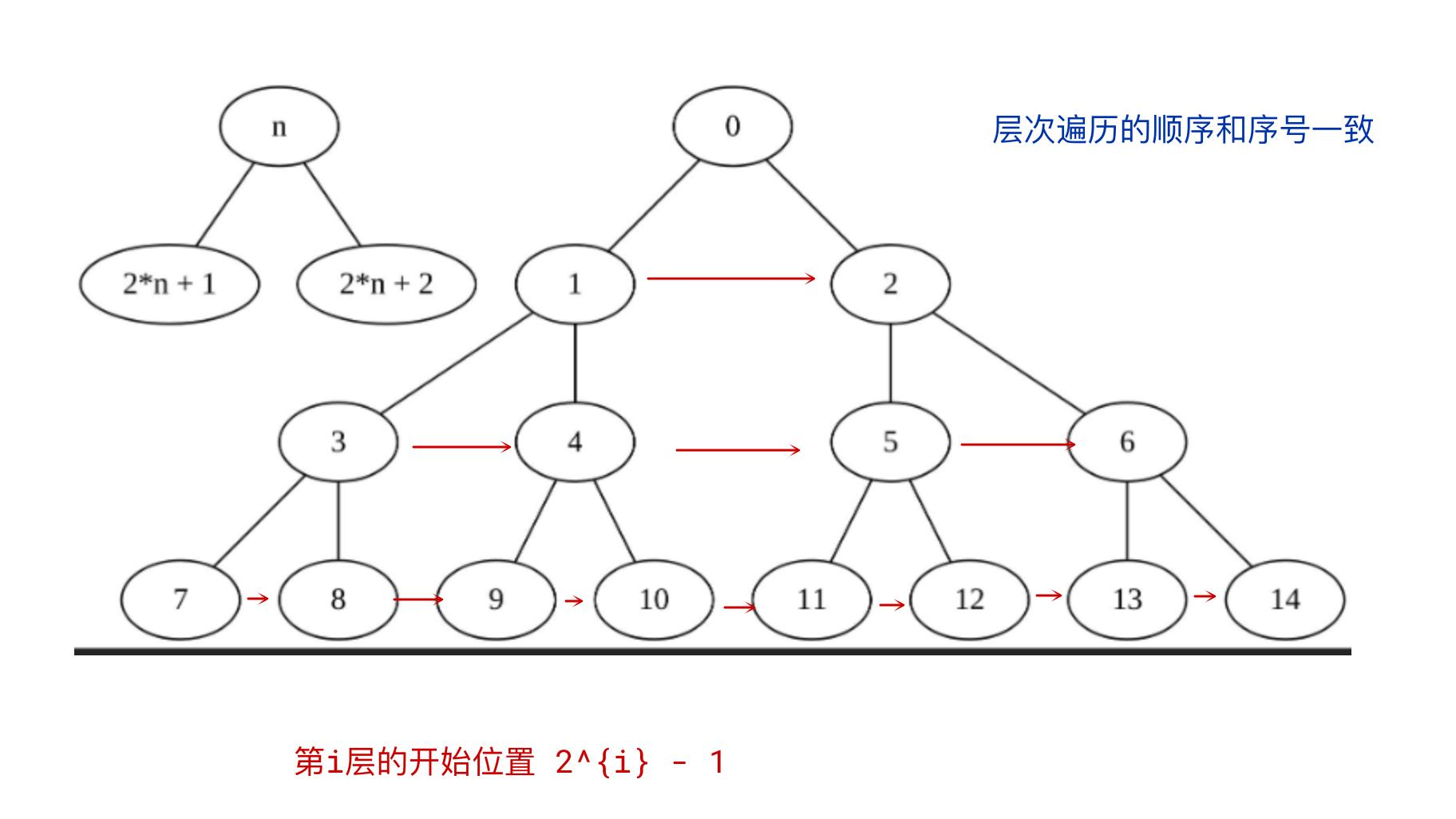
image.png

思路1：BFS:利用下标进行计数

  • 用BFS数组来存储完全二叉树，如果数组大小和数组中最后一个元素的下标相同，那么就是完全二叉树，反之必然不是。
  • 每个元素都有一个自己的编号，代表它是层序遍历中第index个访问到的元素
  • 编号LC958.二叉树的完全性检验 - 图2的节点，其左孩子的编号为LC958.二叉树的完全性检验 - 图3，右孩子编号 LC958.二叉树的完全性检验 - 图4（编号从0开始）
  • 通过node_seq.size() - 1 == 最后一个元素的下标判断是不是完全二叉树
  • 无论什么情况下，假设层数为LC958.二叉树的完全性检验 - 图5，最后一个元素的下标必然是LC958.二叉树的完全性检验 - 图6（因为下标从0开始，实际上就是如果此树是完全二叉树，LC958.二叉树的完全性检验 - 图7）
  • 此题提供了利用数组方式BFS的一种思路，常见的队列方式也可以做，大部分BFS问题两种方法都可以换着来。

image.png

代码1：

  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13. public:
  14.     bool isCompleteTree(TreeNode* root) {
  15.         // 利用标记进行BFS
  16.         vector<pair<TreeNode* ,int>> node_seq;
  17.         node_seq.push_back({root, 0});
  19.         // queue的大小不断变化
  20.         for (int i = 0; i < node_seq.size(); ++i) {
  21.             pair<TreeNode*, int> cur_pos;
  22.             cur_pos.first = node_seq[i].first;
  23.             cur_pos.second = i;
  25.             if (cur_pos.first->left) {node_seq.push_back({cur_pos.first->left, 2 * i + 1});}
  26.             if (cur_pos.first->right) {node_seq.push_back({cur_pos.first->right, 2 * i + 2});}
  27.         }
  29.         // 因为是从0开始的
  30.         return node_seq.size() - 1 == node_seq[node_seq.size() - 1].second;
  31.     }
  32. };

思路2：BFS主流做法，判断之前是否出现过空节点

  • 设置一个have_nullptr判断是不是出现过空节点
  • 如果出现过空节点之后，仍然会出现非空节点，立即返回false
  • 可以通过常规的队列去做，这里采用了按照下标构建数组的方式，大部分BFS问题，两种2方式都可以换着使用

    代码2：

  1. class Solution {
  2. public:
  3.     bool isCompleteTree(TreeNode* root) {
  4.         vector<pair<TreeNode*, int>> nodes;
  5.         nodes.push_back({root, 0});
  7.         bool have_nullptr = false;
  8.         for (int i = 0; i < nodes.size(); i++) {
  9.             pair<TreeNode*, int> cur_node = nodes[i];
  11.             if (cur_node.first->left) {
  12.                 if (have_nullptr) return false;
  13.                 nodes.push_back({cur_node.first->left, 2 * i + 1});
  14.             } else {
  15.                 have_nullptr = true;
  16.             }
  18.             if (cur_node.first->right) {
  19.                 if (have_nullptr) return false;
  20.                 nodes.push_back({cur_node.first->right, 2 * i + 2});
  21.             } else {
  22.                 have_nullptr = true;
  23.             }
  24.         }
  26.         return true;
  27.     }
  28. };

思路3：DFS + 标号

  • 所有节点的数量可以通过dfsCount(root)求出
  • 所有节点可以按照一定顺序来标号（逐层标号，从左到右，没有节点也要占用标号），也就是root.left.val = 2 * root.val + 1, root.right.val = 2 * root.val + 2，记最大标号为maxIndex。

  • 如果maxIndex + 1 == dfsCount(root),就说明是完全二叉树，否则不是。

    代码3：

    1. # Definition for a binary tree node.
    2. # class TreeNode:
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution:
    8.   def __init__(self):
    9.       self.maxIndex = 0
    11.   def dfsCount(self, root: TreeNode) -> int:
    12.       if not root:
    13.           return 0
    14.       if not root.left and not root.right:
    15.           return 1 
    16.       return self.dfsCount(root.left) + self.dfsCount(root.right) + 1
    18.   def recMaxIndex(self, root: TreeNode, curIndex: int) -> None:
    19.       if not root:
    20.           return
    22.       self.maxIndex = max(self.maxIndex, curIndex) 
    23.       self.recMaxIndex(root.left, 2 * curIndex + 1)
    24.       self.recMaxIndex(root.right, 2 * curIndex + 2)
    26.   def isCompleteTree(self, root: TreeNode) -> bool:
    27.       self.recMaxIndex(root, 0)
    28.       return self.maxIndex + 1 == self.dfsCount(root)