题目

思路

https://www.acwing.com/solution/content/16708/

  • 二分查找的核心不是单调性、有序性，而是分段性。这是理解整个二分查找思想的核心。
  • 二分查找分成两种情况，一种称为“左边多型”，即[left, mid]和[mid + 1, right]，一种是“右边多”型”，即[left, mid - 1]和[mid, right]
  • 二者的模板分别如下：所谓check[mid]说明mid位置符合该区间需要的条件最后一个位置

image.png

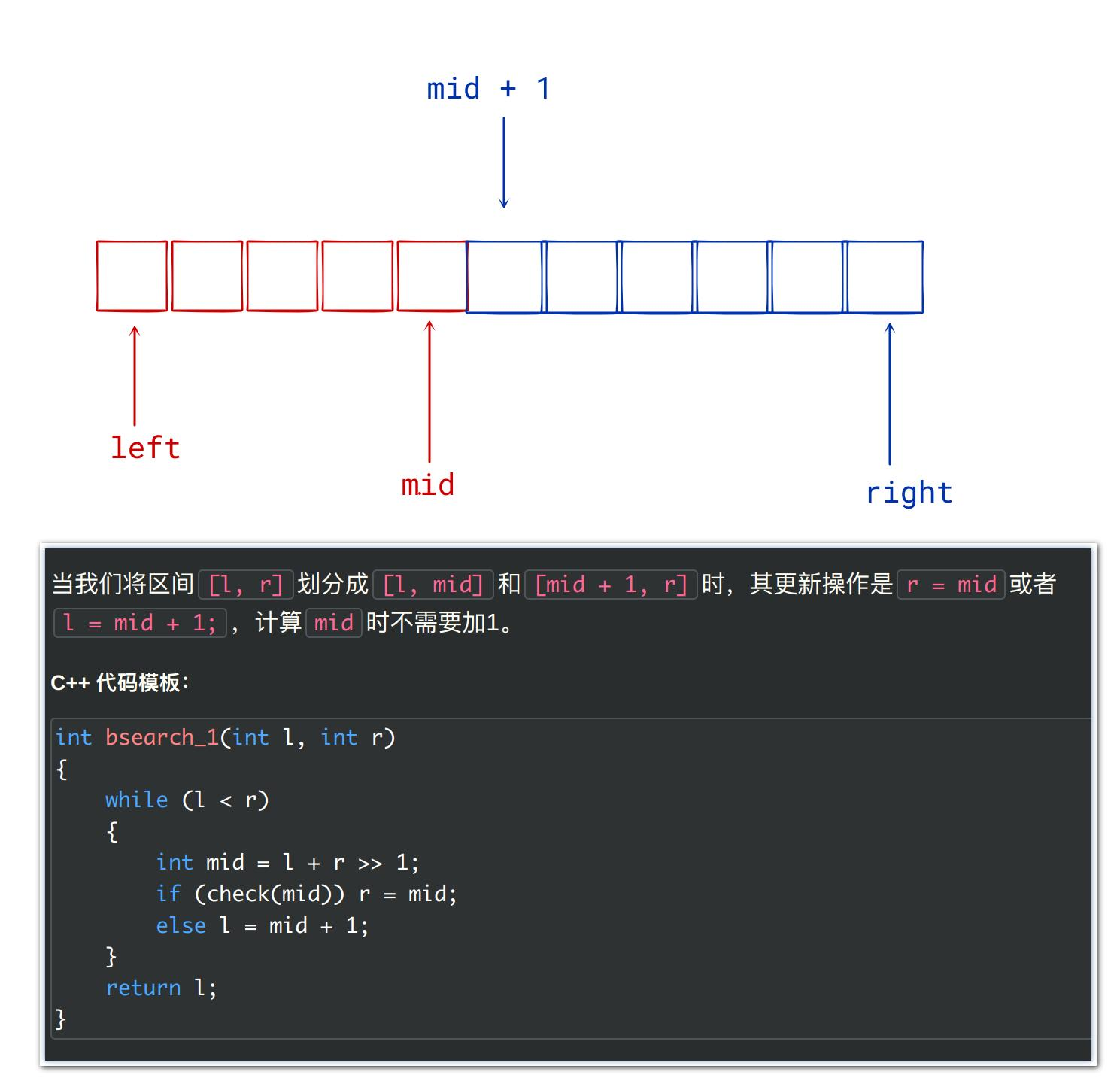
左边多型：如果mid不符合左边的条件，那么 right = mid 最后的返回值代表蓝色的第一个位置

image.png

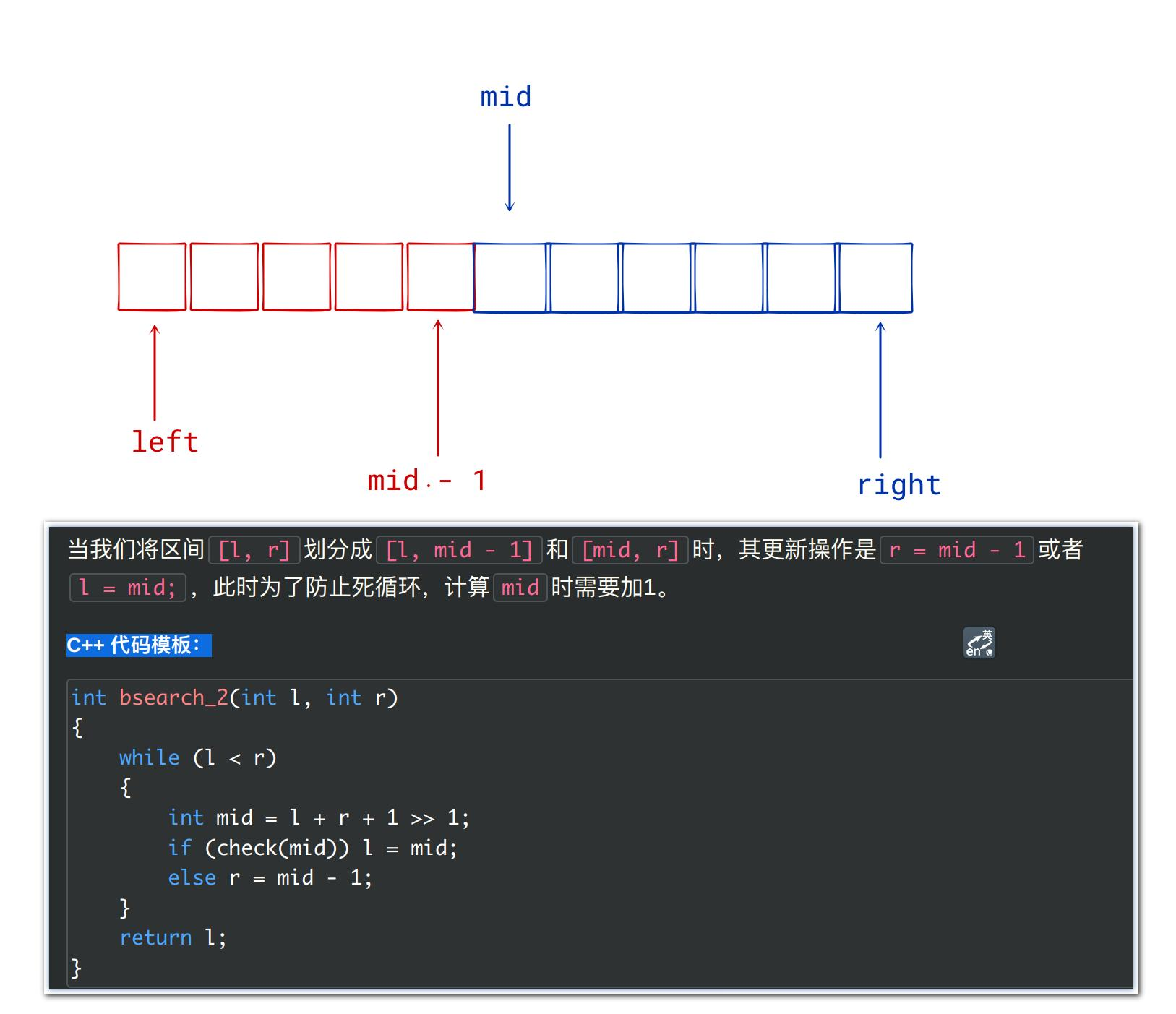
右边多型：如果mid不符合

  • 左边多型：left = mid + 1
  • 右边多型：mid = (left + right + 1) / 2; right = mid - 1
  • 模板可以参考以下代码： ```c

    include

using namespace std;

int main() { int nums[10] = {-1, -1, -1, -1, 1, 1, 1, 1, 1, 1}; // 左边多型:返回右边的最左位置 / int left = 0, right = 10 - 1; while (left < right) { int mid = left + (right - left) / 2; // 如果mid位置符合右边的条件 if (nums[mid] > 0) { right = mid; } else { // 动left, 说明取最左边的位置 left = mid + 1; } } // 返回最左位置 cout << left << “ “ << right << endl; /

  1. int left = 0, right = 10 - 1;
  2. while (left < right) {
  3.     int mid = (left + right + 1) >> 1;
  4.     // 如果mid位置符合左边的条件
  5.     if (nums[mid] < 0) {
  6.         left = mid;
  7.     } else {
  8.         // 动right，说明取最右边的位置
  9.         right = mid - 1;
  10.     }
  11. }
  12. // 返回最右位置
  13. cout << right << endl;
  14. return 0;

}


- 对于这道题而言，左右区间分别指的是：

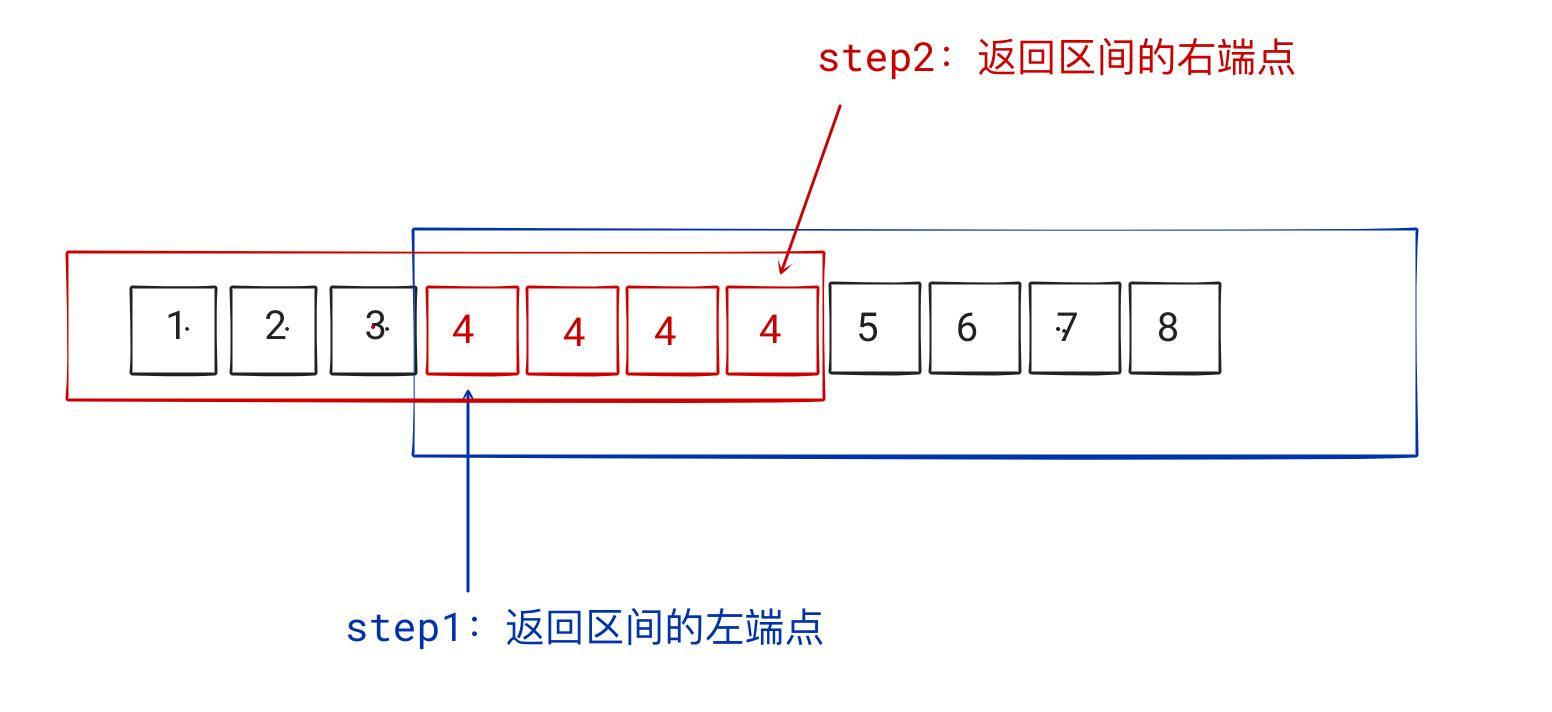
![image.png](https://cdn.nlark.com/yuque/0/2022/png/1626815/1649340441058-4c5ab85e-b600-42eb-b585-9241eb7bf875.png#clientId=uc05d3c2d-c3fb-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=242&id=u95ebcbdf&margin=%5Bobject%20Object%5D&name=image.png&originHeight=712&originWidth=1552&originalType=binary&ratio=1&rotation=0&showTitle=false&size=181455&status=done&style=none&taskId=u87df01a0-b366-4931-a5a9-88c2bce85e0&title=&width=527.4545288085938)

- 左端点：
```cpp
int mid = (right + left) / 2
if (nums[mid] >= k) {
    right = mid;
} else {
    left = mid + 1;
}
  • 右端点：
    int mid = (left + right + 1) / 2
if (nums[mid] <= k) {
  left = mid;
} else {
  right = mid - 1;
}

    代码

    ```cpp

    include

    include

using namespace std;

const int N = 1e6 + 10;

void query(int* nums, int target, int n) { int left = 0, right = n - 1; while (left < right) { int mid = (left + right) / 2; if (nums[mid] >= target) { right = mid; } else { left = mid + 1; } }

if (nums[left] == target) 
    cout << left << " ";
else
    cout << "-1" << " ";

left = 0, right = n - 1;
while (left < right) {
    int mid = (left + right + 1) >> 1;
    if (nums[mid] <= target) {
        left = mid;
    } else {
        right = mid - 1;
    }
}

if (nums[right] == target) 
    cout << right << endl;
else
    cout << "-1" <<  endl;

} int main() { int nums[N]; int n = 0, m = 0; cin >> n >> m; for (int i = 0; i < n; ++i) { cin >> nums[i]; }

for (int i = 0; i < m; ++i) {
    int target = 0;
    cin >> target;
    query(nums, target, n);
}
return 0;

} ```