LC222. 完全二叉树的节点个数

思路

• 一直靠着左边往下走，那么肯定能到最左边的叶子节点
• 问题的关键在于确定剩下的节点数量，等于求最下面一层叶子节点的数量
• 使用二分查找，确定“存在状态”的节点的最右侧（也就是right = mid - 1求右边界的二分查找）
• 现在的问题在于，如何确定节点的存在状态
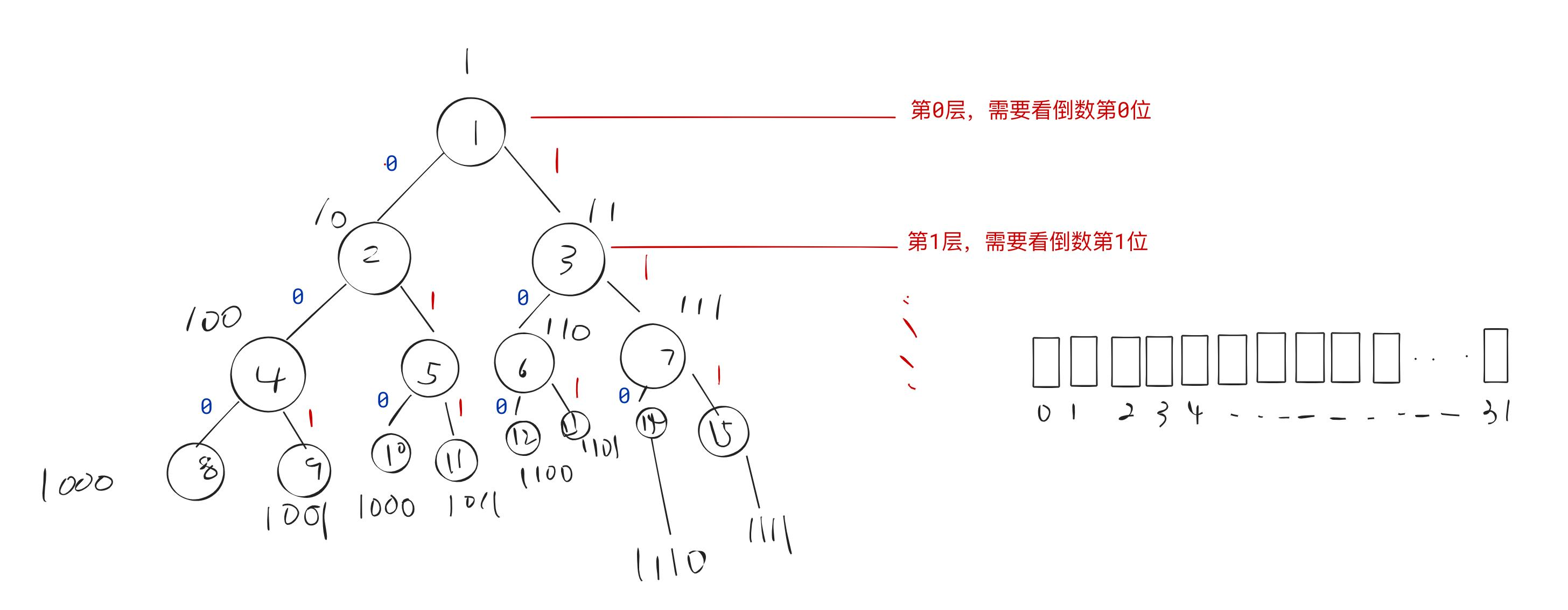
• 可以将节点标号，第0层为1，第1层从左到右10 11，第2层：100 101 110 111，等于按照层次往下标号，走左边就标0，走右边标1。通过序号去遍历这棵树，从而判断是不是存在指定位置的节点。

LC222. 完全二叉树的节点个数

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool exist(TreeNode* root, int num) {
        TreeNode* node = root;
        // 先定位到最高位
        int highest = 0;
        for (int i = 0; i < 31; i++) {
            if (num & (1 << (31 - i))) {
                highest = 31 - i;
                break;
            }
        }
        for (int i = highest - 1; i >= 0; i--) {
            if (node == nullptr) {
                break;
            }
            if (((num >> i) & 1) == 0) {
                node = node->left;
            } else {
                node = node->right;
            }
        }
        return node != nullptr;
    }
    int countNodes(TreeNode* root) {
        TreeNode* node = root;
        if (!root) {
            return 0;
        }
        int level = 0;
        while (node->left) {
            level++;
            node = node->left;
        }
        int left = (1 << level), right = (1 << (level + 1)) - 1;
        while (left < right) {
            int mid = (left + right + 1) / 2;
            if (exist(root, mid)) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return right;
    }
};