LC421.数组中两个数的最大异或值

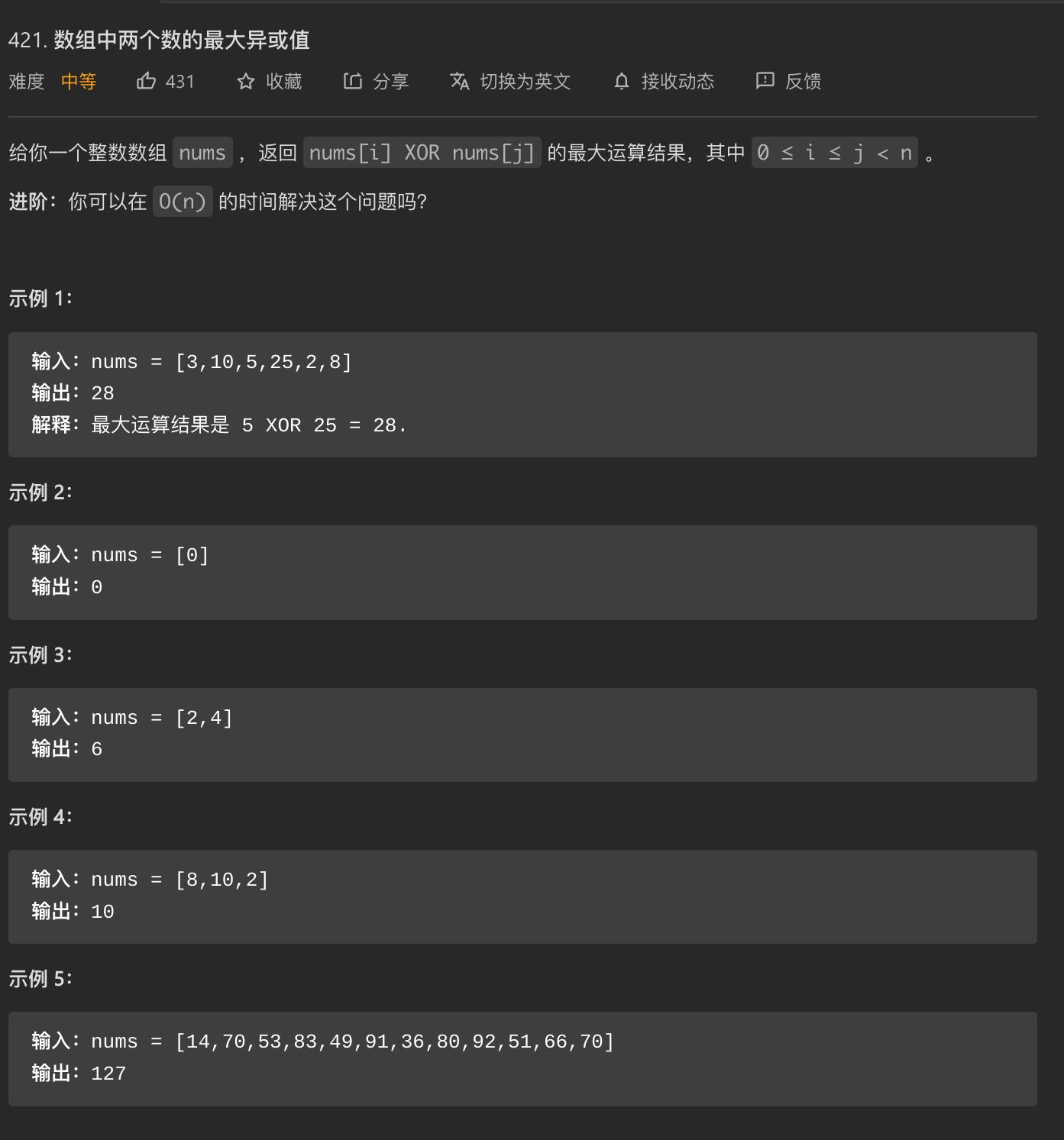
思路：字典树 + 贪心

• 首先建立一棵字典树，高位的节点应该放在离根近的地方，所有的数字都挂在了树上
• 从根节点往下读，选择一个当前的数字num，如果num最高位是1，那么就往0的方向去走。尽可能保证高位的结果是1，读完整棵树就可以了
• 需要注意的是，如何将一个32位的整数，将最左边标为0号，最右边标为31号（从左向右，从0到31标号），(num >> (31 - i)) & 1

代码：

class TrieNode:
    def __init__(self):
        self.children = [None for i in range(2)]
    def insertNum(self, nums: List[int]) -> None:
        for num in nums:
            curNode = self
            for i in range(1, 32):
                curBit = ((num >> (31 - i)) & 1)
                if curNode.children[curBit] == None:
                    curNode.children[curBit] = TrieNode()
                curNode = curNode.children[curBit]
class Solution:
    # 所谓最大值，本质上就是希望两个数字各自能提供尽可能多的'1'
    # 先建一棵树，可以全挂上去（这一步应该有优化，但是我没有想到）
    def traverseTrie(self, node: TrieNode, num: int) -> None:
        maxRes = 0
        for i in range(1, 32):
            curBit = (num >> (31 - i)) & 1
            chooseDirection = curBit ^ 1
            if node.children[chooseDirection] != None:
                node = node.children[chooseDirection]
                maxRes += (1 <<(31 - i))
            else:
                node = node.children[curBit]
        return maxRes
    def findMaximumXOR(self, nums: List[int]) -> int:
        trieRoot = TrieNode()
        trieRoot.insertNum(nums)
        maxRes = 0
        for num in nums:
            maxRes = max(maxRes, self.traverseTrie(trieRoot, num))
        return maxRes