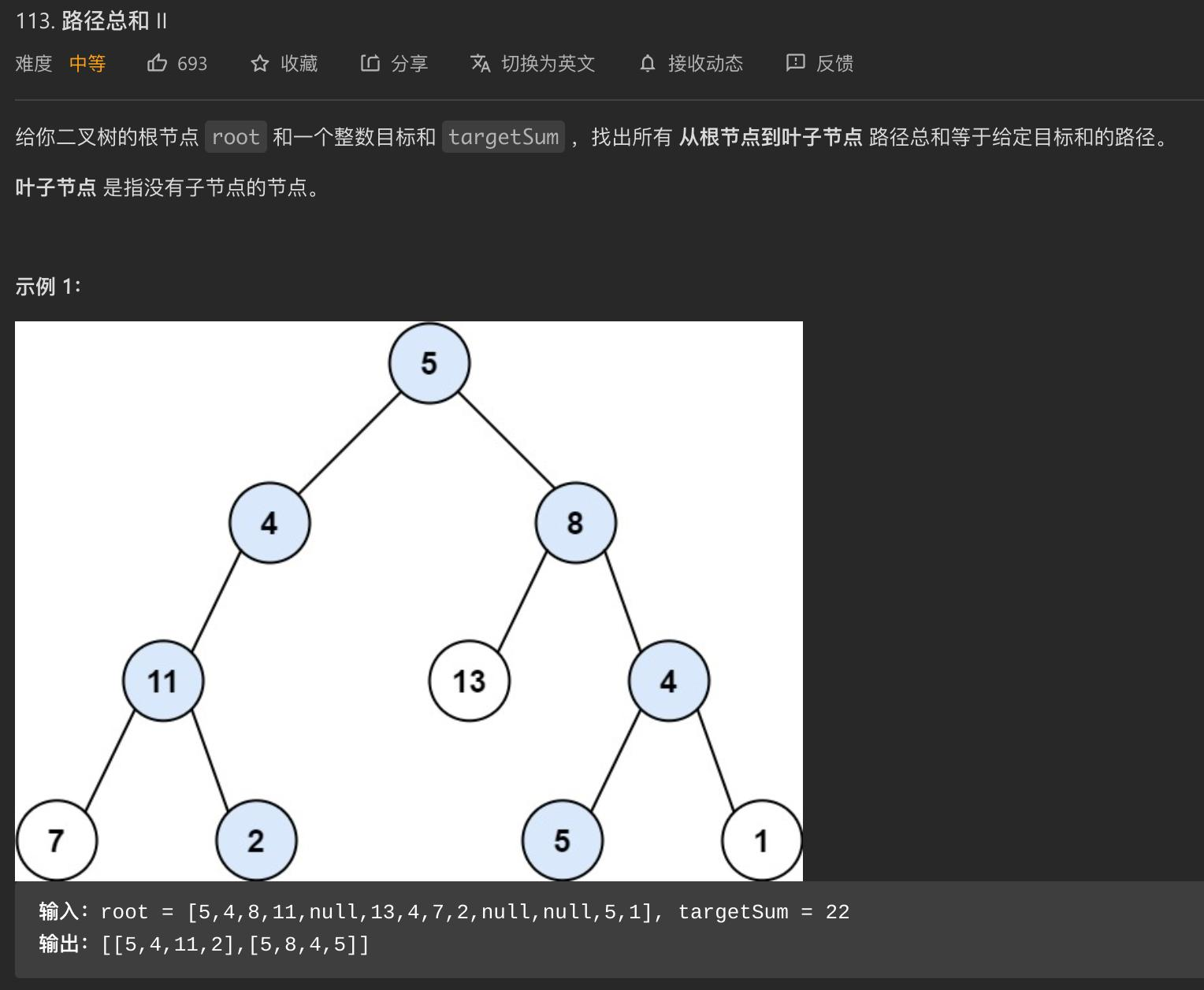
image.png

思路1：回溯

  • cur_path 记录当前路径中的总和
  • 如果在叶子节点上出现了cur_sum == target_sum，就将cur_path放到fit_path当中。否则就进行回溯操作。
  • 回溯的“回”如何实现？cur_path.pop_back()

    代码1：

  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13. public:
  14.     vector<vector<int>> fit_path;
  15.     vector<int> cur_path;
  17.     void traceBack(TreeNode* root, int pre_sum, int targetSum) {
  18.         if (!root) {
  19.             return;
  20.         }
  22.         int cur_sum = pre_sum + root->val;
  23.         cur_path.push_back(root->val);
  24.         if (!root->left && !root->right) {
  25.             if (cur_sum == targetSum) {
  26.                 fit_path.push_back(cur_path);
  27.             }
  28.         }
  29.         traceBack(root->left, cur_sum, targetSum);
  30.         traceBack(root->right, cur_sum, targetSum);
  32.         // 回溯的“回”操作
  33.         cur_path.pop_back();
  35.     }
  36.     vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
  37.         traceBack(root, 0, targetSum);
  38.         return fit_path;
  39.     }
  40. };

思路2：BFS + parents哈希表记录路径

  • 常见的BFS，注意去维护pair结构，这样可以记录当前节点的路径和。儿子不知道爹是谁，但是爹可以提前把信息传给儿子，体现在代码中就是q.push({cur_node->left, cur_sum + cur_node->left->val});
  • 此题可以用哈希表记录父亲节点，因为在BFS的时候，可以传递父子关系，用哈希表记录下来。寻找的时候，通过关系不断往上找，代码即是：
  1. //unordered_map<TreeNode*, TreeNode*> rec_parents
  2. while (cur_node) {
  3.         cur_path.push_back(cur_node->val);
  4.         cur_node = rec_parents[cur_node];
  5. }

代码2：

class Solution {
public:
    vector<int> getPath(TreeNode* cur_node, unordered_map<TreeNode*, TreeNode*> rec_parents) {
        vector<int> cur_path;
        while (cur_node) {
            cur_path.push_back(cur_node->val);
            cur_node = rec_parents[cur_node];
        }
        reverse(cur_path.begin(), cur_path.end());

        return cur_path;
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        unordered_map<TreeNode*, TreeNode*> rec_parents;
        vector<vector<int>> all_path;
        if (!root) {
            return all_path;
        }

        queue<pair<TreeNode*, int>> q;
        q.push({root, root->val});

        while (!q.empty()) {
            TreeNode* cur_node = q.front().first;
            int cur_sum = q.front().second;
            q.pop();

            // 如果是叶子节点
            if (!cur_node->left && !cur_node->right && cur_sum == targetSum) {
                all_path.push_back(getPath(cur_node, rec_parents));
            }

            if (cur_node->left) {
                q.push({cur_node->left, cur_sum + cur_node->left->val});
                rec_parents[cur_node->left] = cur_node;
            }
            if (cur_node->right) {
                q.push({cur_node->right, cur_sum + cur_node->right->val});
                rec_parents[cur_node->right] = cur_node;
            }
        }

        return all_path;
    }
};