LC144.二叉树的前序遍历(todo)

todo: 补齐Morris遍历法，空间复杂度要稍微低一点

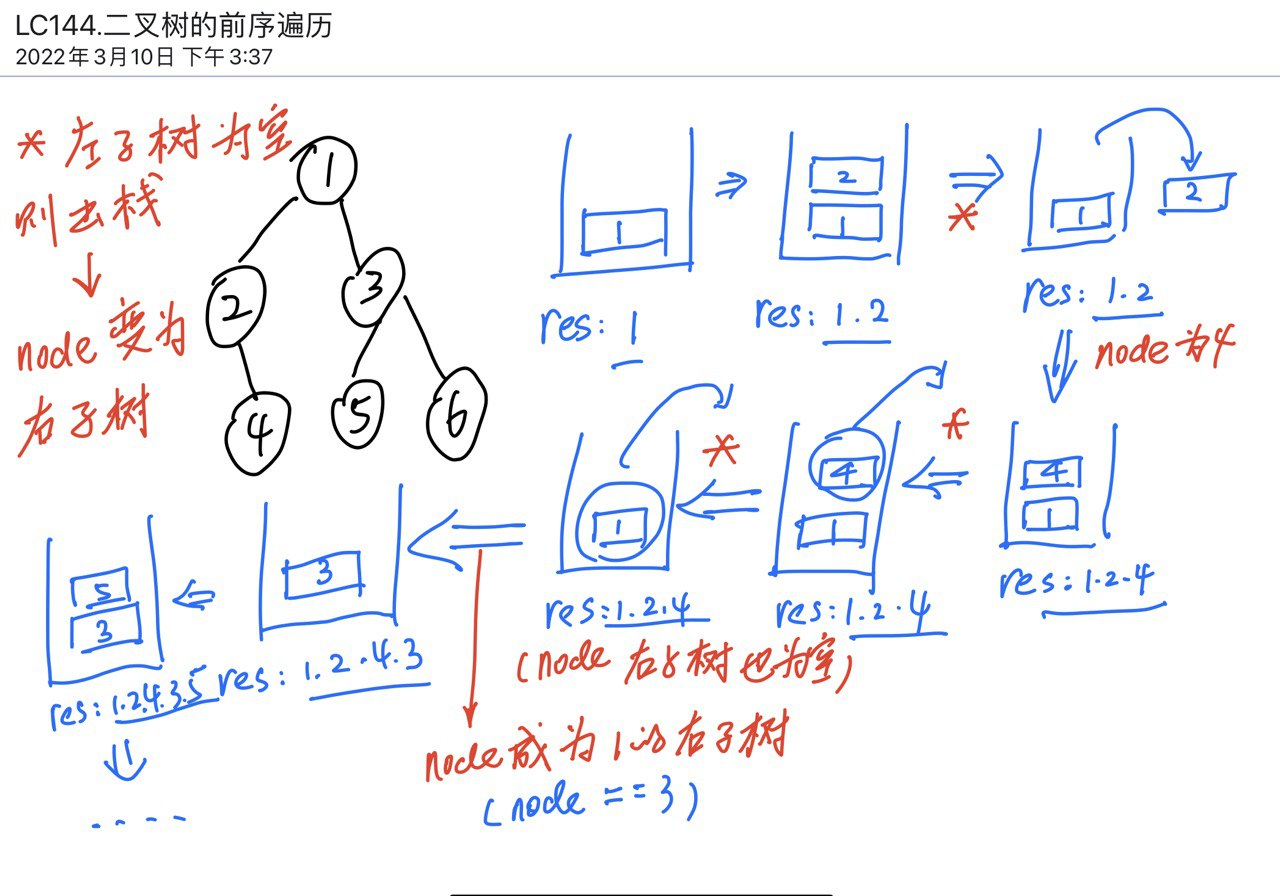
思路1：栈式DFS的实现1（比较繁琐，不推荐）

• 递归的思路就不用多说了
• 关键是栈式dfs的思路
  • 维护两个结构，一个是node_stack()，另外一个是preorder_sequence,入栈的时候同步添加序列，这就意味着谁先入栈，就先遍历到谁
  • 先序遍历中，优先选择左边的子树入栈，这样可以保证优先遍历中序节点
  • 出栈条件是什么？如果左边的子树为空，就将cur_node指向最近的一个有右节点的节点，实际操作就是cur_node = nodes_stack.top()，并且弹栈。
  • 要能够画出入栈弹栈的整个流程图。脑子里要有图。
  • 实际的操作是比较零碎复杂的，最好能够记住模板。

代码1：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> preorder_sequence;
        stack<TreeNode*> nodes_stack;
        if (!root) {
            return preorder_sequence;
        }
        TreeNode* cur_node = root;
        while (!nodes_stack.empty() || cur_node != nullptr) {
            // 弹栈条件：left子树为空
            while (cur_node != nullptr) {
                nodes_stack.push(cur_node);
                preorder_sequence.push_back(cur_node->val);
                cur_node = cur_node->left;
            }
            // cur_node 需要指向最近的一个right子树不为空的节点
            cur_node = nodes_stack.top();
            nodes_stack.pop();
            cur_node = cur_node->right;
        }
        return preorder_sequence;
    }
};

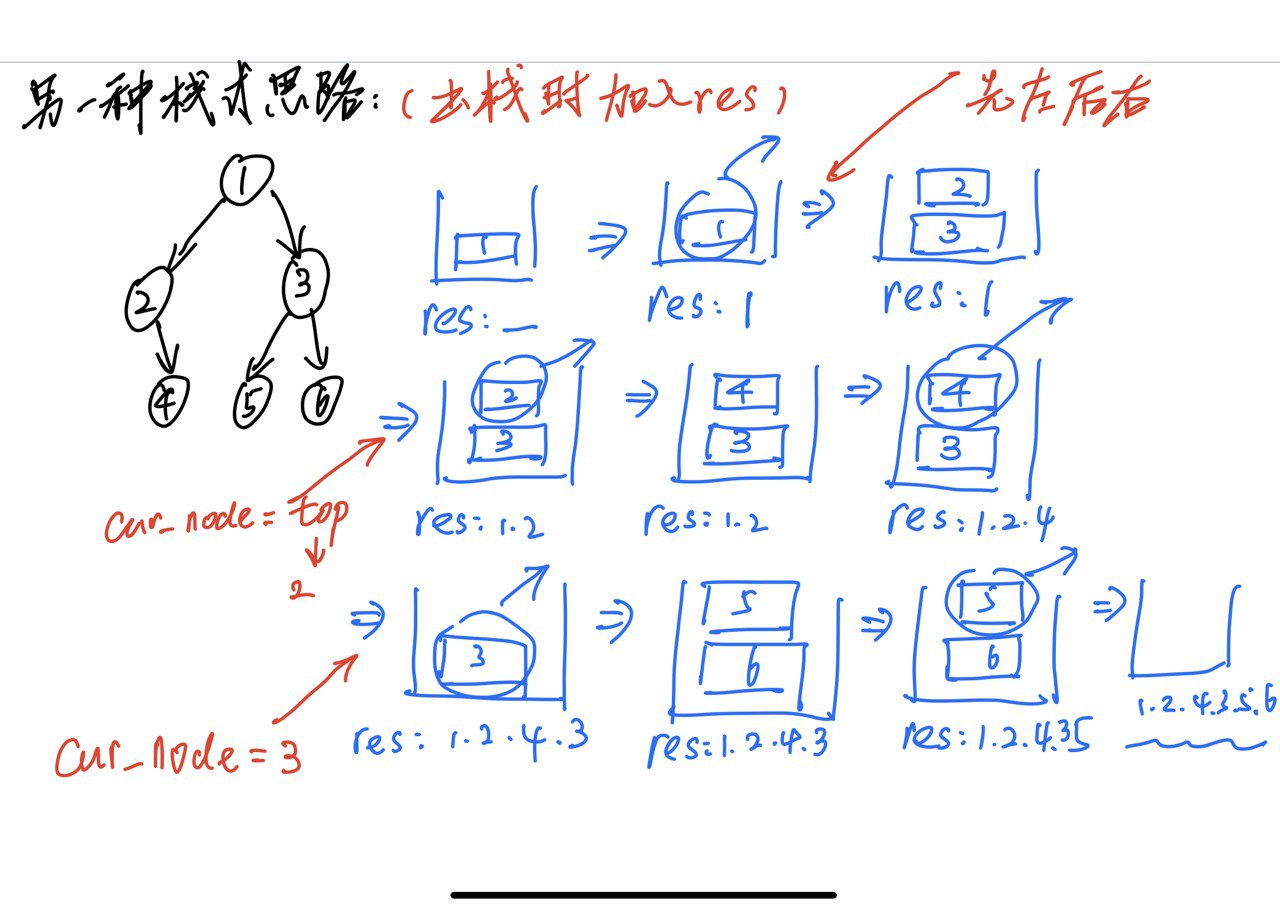
思路2：栈式DFS的实现2（推荐）

• 第一种思路采取的思路是入栈的时候同步插入序列，先入栈者先进入遍历序列。
• 此处采用的思路是出栈的时候插入遍历序列，所以若希望先进入遍历序列，则应该后入栈，所以优先将右侧的节点入栈。
• 还是需要脑子里面有图。结合代码去理解。

代码2：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> nodes_stack;
        vector<int> nodes_sequence;
        if (!root) {
            return nodes_sequence;
        }
        nodes_stack.push(root);
        while(!nodes_stack.empty()) {
            TreeNode* cur_node = nodes_stack.top();
            nodes_stack.pop();
            nodes_sequence.push_back(cur_node->val);
            if (cur_node->right) {nodes_stack.push(cur_node->right);}
            if (cur_node->left) {nodes_stack.push(cur_node->left);}
        }
        return nodes_sequence;
    }
};