image.png

思路：

https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/trie-tree-de-shi-xian-gua-he-chu-xue-zhe-by-huwt/ 参考此题解，写的非常好

  • 前缀树又称字典树，用来快速查询新的字符串是否在当前的字典中，如果没有，就将其插入到字典中。用途就是模糊搜索（比如代码补全），本质上是一棵26叉树。
  • 对于树中的每一个节点，其数据结构都是一个bool数据 + 26个分叉指针。如果父亲节点的子节点不为空，说明该子节点索引对应的字符存在字典中。
  1. bool is_end;
  2. Trie* next[26];

image.png
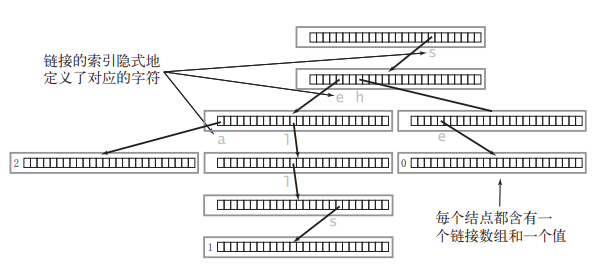
为了便于逻辑上的理解，主流的画法是不画出空节点。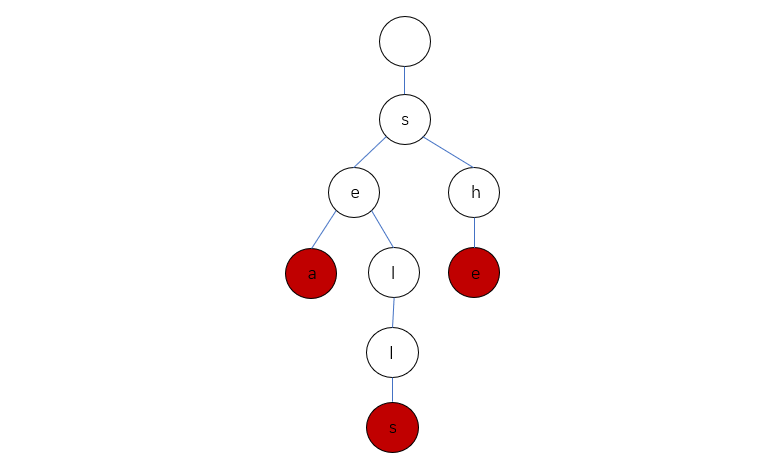
image.png

  • 分成两个操作：插入、查询
  • 插入操作，一直往下搜索，如果遇到nullptr，就逐个把剩下的字符插入到字典树当中
  1. void insert(string word) {
  2.         Trie* node = this;
  3.         for (char ch: word) {
  4.             if (node->next[ch - 'a'] == nullptr) {
  5.                 // 父亲节点有子节点了，就说明当前位置存储了子节点索引所对应的字符
  6.                 node->next[ch - 'a'] = new Trie();
  7.             }
  8.             node = node->next[ch - 'a'];
  9.         }
  10.         node->is_end = true;
  11.     }
  • 查询操作更加直观，顺着数组中的每一个字母不断往下搜索，如果遇到了nullptr，那么就说明数组中的所有字符并没有完全存在字典树当中，返回false，如果读完了整个数组，那么还要判断当前位置的is_end，说不定现在的数组，只是之前的字典树中存储的记录的一部分呢。
  1. bool search(string word) {
  2.         Trie* node = this;
  3.         for (char ch: word) {
  4.             node = node->next[ch - 'a'];
  5.             if (node == nullptr) {
  6.                 return false;
  7.             }
  8.         }
  10.         return node->is_end;
  11.     }
  • 搜索前缀更加简单，和普通搜索差不多，最后改成返回true即可。
  1. bool startsWith(string prefix) {
  2.         Trie* node = this;
  3.         for (char ch: prefix) {
  4.             node = node->next[ch - 'a'];
  5.             if (node == nullptr) {
  6.                 return false;
  7.             }
  8.         }
  9.         return true;
  10.     }

代码：

  1. class Trie {
  2. private:
  3.     bool is_end;
  4.     Trie* next[26];
  5. public:
  6.     Trie() {
  7.         is_end = false;
  8.         memset(next, 0, sizeof(next));
  9.     }
  11.     void insert(string word) {
  12.         Trie* node = this;
  13.         for (char ch: word) {
  14.             if (node->next[ch - 'a'] == nullptr) {
  15.                 // 父亲节点有子节点了，就说明当前位置存储了子节点索引所对应的字符
  16.                 node->next[ch - 'a'] = new Trie();
  17.             }
  18.             node = node->next[ch - 'a'];
  19.         }
  20.         node->is_end = true;
  21.     }
  23.     bool search(string word) {
  24.         Trie* node = this;
  25.         for (char ch: word) {
  26.             node = node->next[ch - 'a'];
  27.             if (node == nullptr) {
  28.                 return false;
  29.             }
  30.         }
  32.         return node->is_end;
  33.     }
  35.     bool startsWith(string prefix) {
  36.         Trie* node = this;
  37.         for (char ch: prefix) {
  38.             node = node->next[ch - 'a'];
  39.             if (node == nullptr) {
  40.                 return false;
  41.             }
  42.         }
  43.         return true;
  44.     }
  45. };
  47. /**
  48.  * Your Trie object will be instantiated and called as such:
  49.  * Trie* obj = new Trie();
  50.  * obj->insert(word);
  51.  * bool param_2 = obj->search(word);
  52.  * bool param_3 = obj->startsWith(prefix);
  53.  */