LC1248.统计优美子数组

思路1：滑动窗口

第一反应就是滑动窗口，但是后续没什么思路，参考了甜姨@sweetiee的做法，这个博主题解写的挺清楚的。读了其他几篇题解，很清晰，推荐。
设置一个滑动窗口，odd_cnt记录窗口内部的奇数数量。指向滑动窗口右边界的指针right从左向右遍历整个数组，逐个填入nums[right]，如果odd_cnt == k，那么就移动左边界指针left，使得left指向“滑动窗口区间的第一个奇数”，那么，[left, right]形成的滑动窗口当中，一定有k个奇数。想要窗口滑动，就将left指向“第一个奇数”的下一个位置，此时odd_cnt == k - 1，产生滑动。
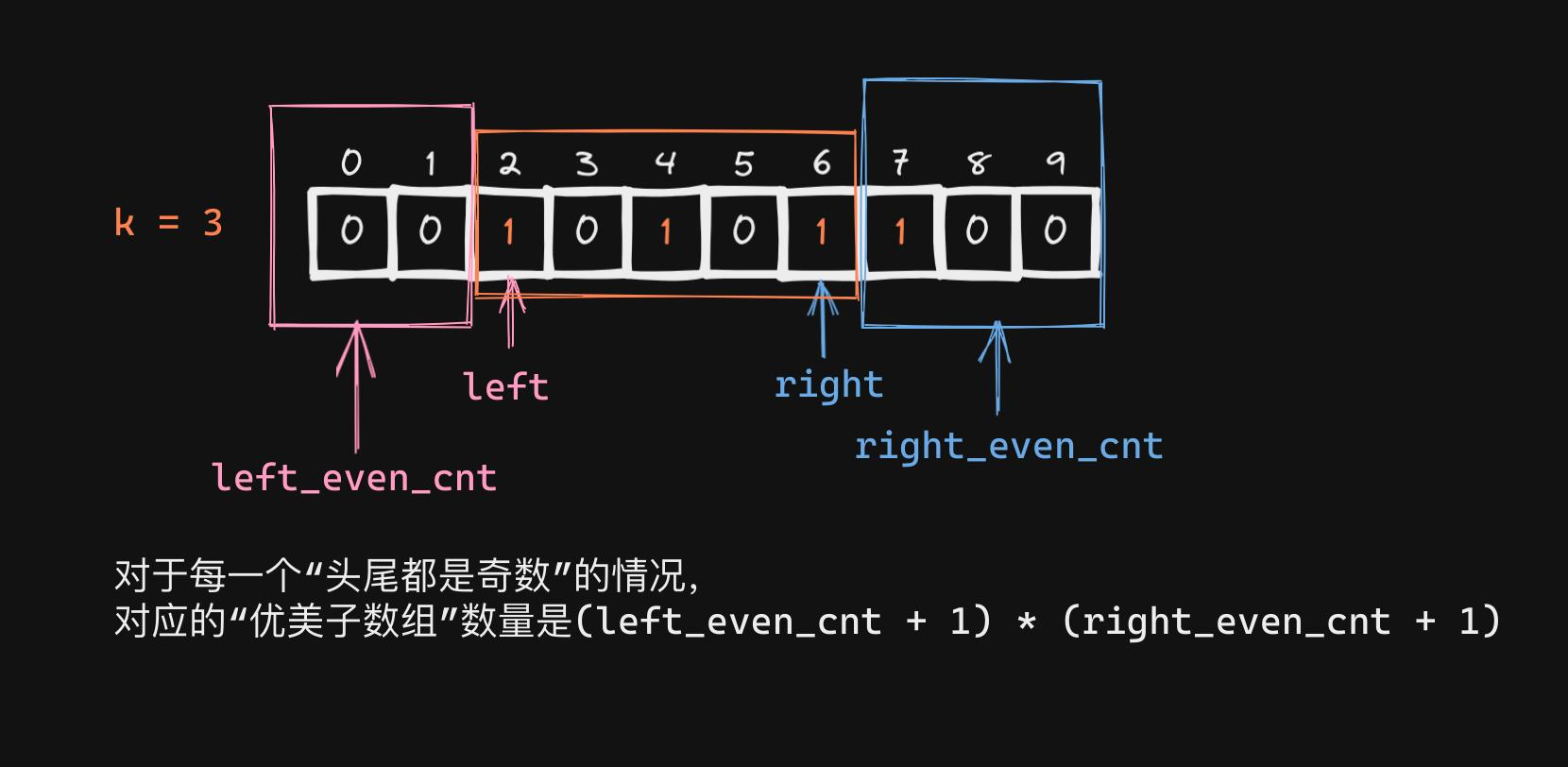
滑动窗口可以不重不漏记录每一个“以left为左边界，right为右边界，且odd_cnt == k”的情况。每一个这种情况都对应若干的“优美子数组”，其统计方式如下。
在left左边的连续的偶数，都可以作为优美子数组的起点。连续偶数的数量记为left_even_cnt。在right右边的连续的偶数，都可以作为优美子数组的终点。连续偶数的数量记为right_even_cnt。

每一个滑动窗口对应的优美子数组的数量为 LC1248.统计优美子数组 - 图3 ，加的那个1说明什么都不取。

代码1：

class Solution {
public:
  int numberOfSubarrays(vector<int>& nums, int k) {
      int n = nums.size(); 
      int left = 0, right = 0;
      int ans = 0;
      int cnt_odd = 0;
      for (right = 0; right < n; right++) {
          // 如果是奇数
          if (nums[right] & 1) {
              cnt_odd += 1;
          }
          // 如果有k个奇数了
          int rp = right + 1;
          int right_even_cnt = 0, left_even_cnt = 0;
          if (cnt_odd == k) {
              // 从当前right指向的位置，到下一个奇数出现的位置（或者数组的最后一个位置），偶数数量记作right_even_cnt
              while ((rp < n) && ((nums[rp] & 1) == 0)) {
                  rp += 1;
                  right_even_cnt += 1;
              }
              // left指向当前数组第一个奇数所在的位置
              while ((nums[left] & 1) == 0) {
                  left_even_cnt += 1;
                  left += 1;
              }
              ans += (left_even_cnt + 1) * (right_even_cnt + 1);
              // 此时left指向数组中第一个奇数，需要往后移动一位。
              left += 1;
              cnt_odd -= 1;
          }
      }
      return ans;
  }
};

思路2：前缀和 + 哈希表

如果奇数记为1，偶数记为0。那么，此题相当于在找“和为k的子数组”。
建立前缀和数组summ。对于在数组当中找
哈希表解决两数之差的问题。哈希表rec，rec[summ[i]]表示summ[i]出现的次数。

对于每一个summ[i]而言，都有rec[summ[i] - k]个summ[j]能够和其匹配，满足 LC1248.统计优美子数组 - 图5 。

代码2：

class Solution {
public:
  int numberOfSubarrays(vector<int>& nums, int k) {
      // 前缀和 + 哈希表
      // 偶数记为0，奇数记为1，等于统计和为k的子数组数量。
      int n = nums.size();
      vector<int> summ(n + 1, 0);
      for (int i = 0; i < n; i++) {
          if (nums[i] & 1) {
              nums[i] = 1;
          } else {
              nums[i] = 0;
          }
      }
      for (int i = 1; i <= n; i++) {
          summ[i] = summ[i - 1] + nums[i - 1];
      }
      unordered_map<int, int> rec;
      int ans = 0;
      for (int i = 0; i <= n; i++) {
          if (rec.count(summ[i] - k)) {
              ans += rec[summ[i] - k];
          }
          rec[summ[i]] += 1;
      }
      return ans;
  }
};