LC462.最少移动次数使数组元素相等II

原题链接

给你一个长度为 的整数数组 ，返回使所有数组元素相等需要的最少移动数。在一步操作中，你可以使数组中的一个元素加 或者减 。

• 示例 1：

  输入：nums = [1,2,3]
  输出：2
  解释：
  只需要两步操作（每步操作指南使一个元素加 1 或减 1）：
  [1,2,3]  =>  [2,2,3]  =>  [2,2,2]

• 示例 2：

  输入：nums = [1,10,2,9]
  输出：16
  

• 提示：

  • 
  • 
  • 

    思路：

• 前缀和优化，复杂度

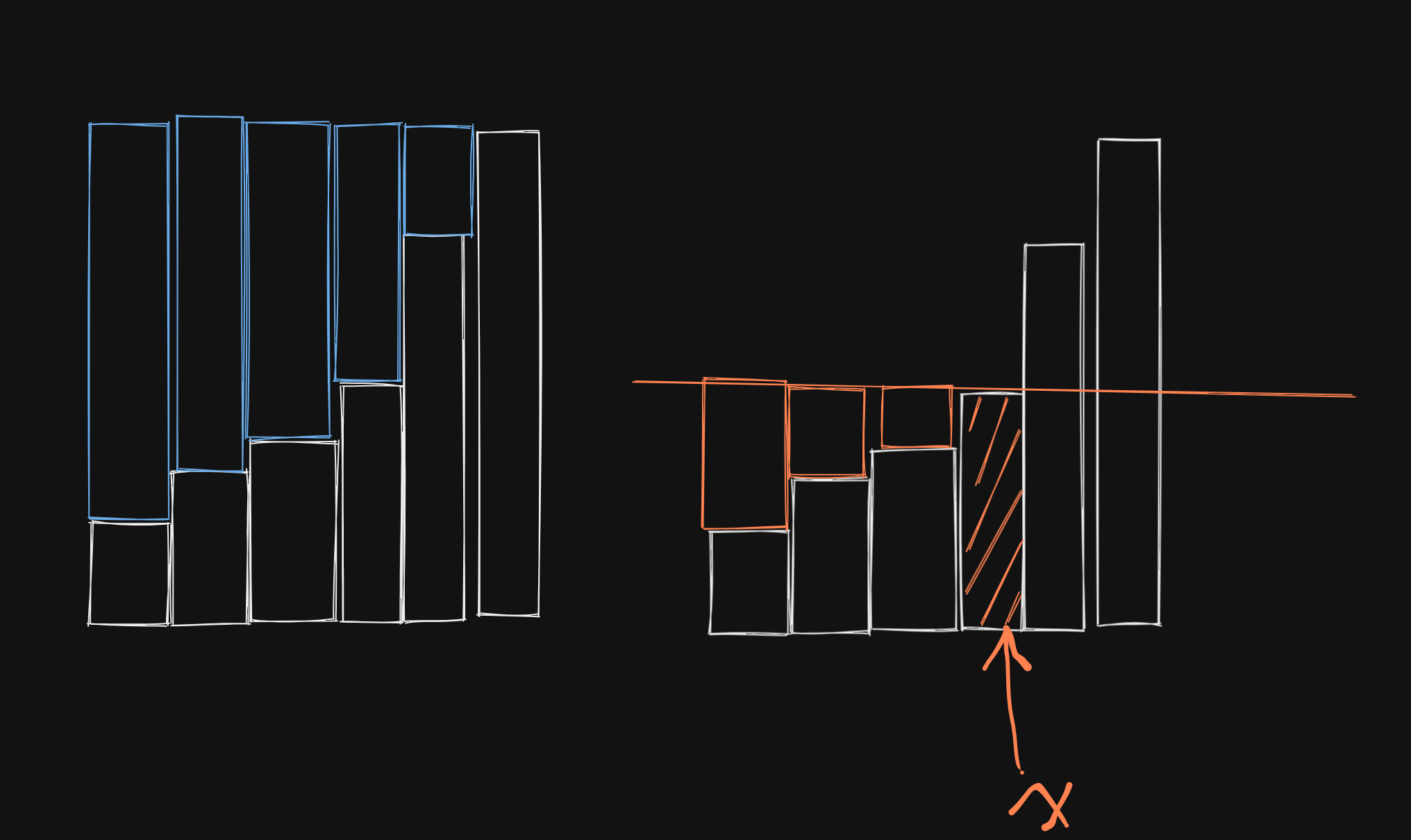
• 首先将数组排序，如果需要将数组内部所有的数全部变成nums[x]，那么，操作次数可以分成左边和右边两部分。
• 对于左边，操作数量等于长方形面积 - 部分前缀和，即nums[x] * x - summ[x]，下标为x，说明从数组开头，不包括x自己，一共x个元素。

• 对于右边，操作数量等于部分前缀和 - 长方形面积，即(summ[n] - summ[x]) - (nums[x] * (n - x))

  代码：

  class Solution {
  public:
    int minMoves2(vector<int>& nums) {
        vector<long long> lnums(nums.size(), 0);
        int n = lnums.size();
        for (int i = 0; i < n; i++) {
            lnums[i] = (long long)nums[i];
        }
        sort(lnums.begin(), lnums.end());
        vector<long long> summ(n + 1, 0);
        for (int i = 1; i <= n; i++) {
            summ[i] = summ[i - 1] + lnums[i - 1];
        }
  
        long long res = INT_MAX;
        for (int i = 0; i < n; i++) {
            long long left_part = (lnums[i] * i) - (summ[i]);
            long long right_part = (summ[n] - summ[i]) - (lnums[i] * (n - i));
            res = min(res, left_part + right_part);
        }
  
        return res;
    }
  };