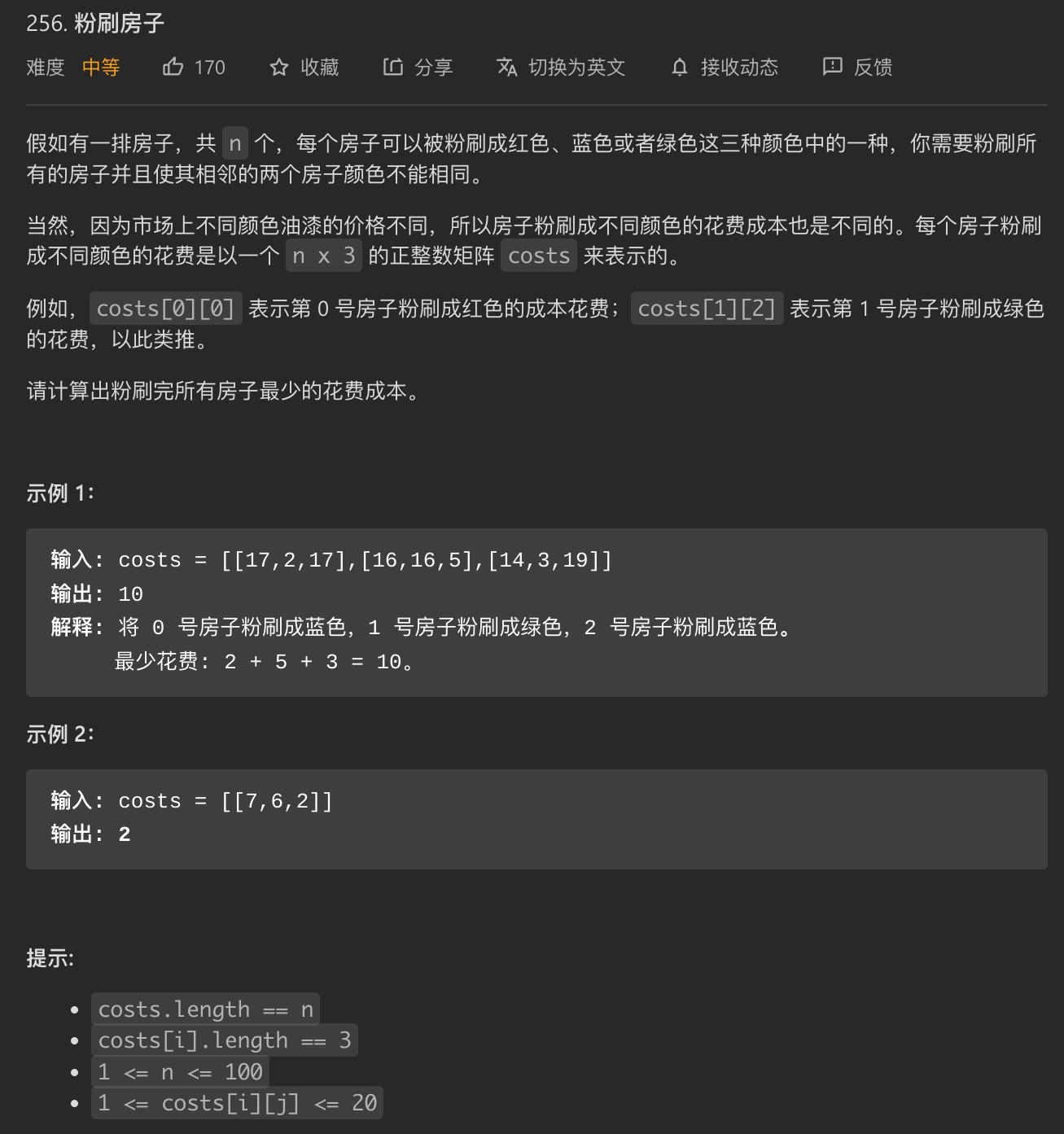
题目

image.png

思路

  • 不需要考虑从开始位置到当前位置的最小花销，状态难以确定。因为当前位置会影响下一个位置，就算当前位置取到了最优，那么如果综合了下一个位置去考虑，可能当前的选择就不是最优了。比如说，当前选了红色，发现开销最小，但是下一个位置可能也是红色，如果无法选取，那么整体来讲当前位置选红色并不是最好的。
  • 如果当前位置确定了颜色，那么上一个位置的颜色一定也会被确定（不重复 + 开销小），顺序递推下去，就可以确定整体的序列。
  • to_red表示[0, i - 1]序列当中，最后一个颜色选择红色，序列的整体最小开销。
  • 当前颜色选择绿色的最小开销为costs[0][1] + min(to_red, to_blue)
  • 关键在于确定状态转移方程的唯一性，不要出现前后干扰等情况。

    代码

  1. class Solution {
  2. public:
  3.     int minCost(vector<vector<int>>& costs) {
  4.         int to_red = costs[0][0], to_blue = costs[0][1], to_green = costs[0][2];
  5.         int n = costs.size();
  6.         for (int i = 1; i < n; ++i) {
  7.             int nxt_to_red = costs[i][0] + min(to_blue, to_green);
  8.             int nxt_to_blue = costs[i][1] + min(to_red, to_green);
  9.             int nxt_to_green = costs[i][2] + min(to_red, to_blue);
  10.             to_red = nxt_to_red;
  11.             to_blue = nxt_to_blue;
  12.             to_green = nxt_to_green;
  13.         }
  15.         return min(to_red, min(to_blue, to_green));
  16.     }
  17. };